Skip to main content
Printable page generated Wednesday, 16 October 2024, 6:16 AM
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Unless otherwise stated, copyright © 2024 The Open University, all rights reserved.
Printable page generated Wednesday, 16 October 2024, 6:16 AM
 TI-AIE: Using visualisation: algebraic identities

TI-AIE: Using visualisation: algebraic identities

What this unit is about

Algebraic identities play an important role in the mathematics curriculum and in mathematics in general. In Class IX in the Indian secondary school curriculum, eight types of identities are used when solving equations and polynomials. Knowing and recognising these identities helps students to learn mathematical procedures. It will also enable them to develop fluency when applying these procedures in algebraic manipulations and problem solving. In order to use the power of identities fully, it is important to be able to spot variations in the algebraic identities. The main issue when learning and applying identities is that, for most students, the work is purely a question of memorising and regurgitating them.

This unit will explore some different approaches using visual representation that you can use with your students to help them learn algebraic identities. These approaches rely less on memorisation and instead build on understanding the concepts of identities.

What you can learn in this unit

  • How to use images to help your students explore and discover how identities are formed.
  • Some ideas on how to use and apply identities without having to rely on memory.
  • How to adjust existing tasks to allow your students to focus on the process of doing mathematics.

This unit links to the teaching requirements of the NCF (2005) and NCFTE (2009) outlined in Resource 1.

1 Learning through memorisation

Learning through memorisation, or rote learning, is a learning technique based on repetition.

There are several arguments in favour of this learning approach: one is that having a rapid recall of certain facts in mathematics is necessary to become fluent in other mathematics topics.

Many students are encouraged to learn their ‘times tables’ by rote. This is so that when they are solving problems they do not spend too much time and effort working out relatively simple calculations such as 6 x 7 – especially when they have no access to calculators. Knowing times tables by heart also gives them a better number sense; for example, of the numbers’ magnitude, of how numbers are related or of multiples and fractions. Similar arguments could be used for learning algebraic identities through memorisation.

However, there are also many counter-arguments to using memorisation as a learning technique (De Morgan, 1865; Marton and Booth, 1997). One is about accessibility; not all students benefit from memorisation due to their poor school attendance, their lack of time or opportunity for the required practice, or just their poor recall. Students with special educational needs such as dyslexia, for example, are enormously disadvantaged.

Another argument concerns the kind of learning that memorisation affords. Memorisation does not focus on comprehension or building understanding; nor does it support any exploration of what concepts could mean, or how they are connected to other areas of mathematics. It focuses on memorising and accurate reproduction, which can become problematic when studying more complex aspects of a subject (such as formulae and algorithms) that entail many steps. Memorisation does not lead to understanding of meaning, which means that elements get missed out, details get muddled up, stress increases and exams can be failed.

The learning experience when using memorisation is often not exciting; it can even be considered boring because of its repetitive nature and lack of focus on understanding and making connections. Students mechanically ‘go through’ the exercises, engaging their brains as little as possible. This is problematic for all students, including high achievers. Boredom when learning mathematics, little demand for thinking and a lack of opportunity to work on making connections and giving meaning to mathematics makes it hard for learners to understand and enjoy the subject.

Pause for thought

  • What are your thoughts about learning through memorisation? Do you think it works well always, sometimes or not often?
  • How did you experience learning mathematics by memorisation?
  • Think of one of your students who seems to be memorising well, and think of one that is struggling. What is the same and what is different about how they learn?

2 Visualisation for developing understanding of algebraic identities

An effective way to rely less on memory for learning is through the use of visualisation. Visualisation means seeing an image of something in your mind. Different people will not always ‘see’ things in the same way, but ‘visual thinking’ is very important to the construction of understanding by your students (Dörfler, 1991).

Visualisation can be introduced with relatively simple operations. For example, multiplication can be represented as a product table that is similar to area. (There are other ways to represent multiplication.)

The product 7 × 3 can be represented by an area of seven by three squares (Figure 1). From this image it is also clear that multiplication is commutative – that is, the product of 7 × 3 is the same area as the product of 3 × 7.

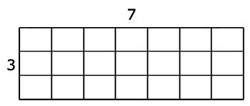
Figure 1 A product table for the sum 7 × 3.

So 7 × 3 is equivalent to 3 × 7 is equivalent to 21. This can be written as:

7 × 3 ~ 3 × 7 ~ 21

Modelling multiplication can help your students to understand a multiplication problem, because the area of a large rectangle can be easily decomposed into areas of smaller rectangles. It is good practice not to draw the area models in proportion to the numbers used: it stimulates more abstract representations and makes the mental jump to representing negative numbers less difficult. Because it is not possible to have a negative area, this kind of representation is referred to as a ‘product table’.

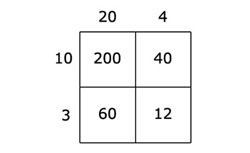
For example, 24 × 13 can be represented by the product table in Figure 2. Hence 24 × 13 ~ (20 + 4) × (10 + 3) ~ 200 + 40 + 60 + 12 ~ 312.

Figure 2 A product table for the sum 24 × 13.

In another example, 192 can be represented by the product table in Figure 3. Hence 192 ~ (20 - 1) × (20 - 1) ~ 400 - 20 - 20 + 1 ~ 361.

Figure 3 A product table for the sum 192.

This decomposition model is very helpful for finding products of larger numbers or for multiplication involving algebra. A simple example involving algebra is 3(a - b), as shown in Figure 4. Hence 3(a - b) ~ 3a - 3b.

Figure 4 A product table for 3(a – b).

You might have noticed that in these examples the equivalence sign (~) has sometimes been used instead of the equals sign (=), which would be equally valid. The equivalence sign can offer a certain freedom, playfulness to mathematics, in particular if the sign is read as ‘is another way of saying’ instead of ‘is equivalent to’.

Activity 1 will support students in working with visualisation by seeing multiplication as a product table. Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, because that will help you when you reflect on the experience.

Trying the activities yourself will mean you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, read Case Study 1 and use the activities with your students. After the lesson, think about the way that the activity went and the learning that happened. This will help you to develop a more learner-focused teaching environment.

Activity 1: Making product tables

Tell your students how to construct product tables modelling a number of examples. You can use ideas from Case Study 1 (below) to help you.

Then write these problems on the board:

  • (105)2
  • (14.3)2
  • 4(99)
  • 982
  • 7(t + r)
  • (r + q)(s - r)

For each of these problems, ask your students to work in pairs to:

  • a.model the problem as a product table
  • b.if appropriate, decompose the area into smaller areas
  • c.work out the products of these calculations by using your answers to (a) and (b).

After the lesson, use the prompts in the ‘Pause for thought’ box below to help you evaluate your teaching in the lesson.

Case Study 1: Mrs Aparajeeta reflects on using Activity 1

This is the account of a teacher who tried Activity 1 with her secondary students.

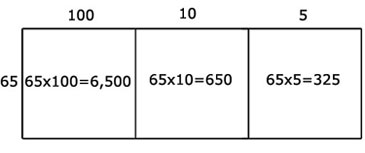
Before starting on this activity we had a discussion on how a number that is squared or multiplied could be represented by an area model, mimicking the way I learned it from reading this unit. I started with small numbers like 5 x 6 and then to bigger numbers like 56 × 64 and 65 × 115. Anup thought of using the distributive property for the question 65 × 115 = 65(100 + 10 + 5), and so he went ahead and represented it as a one-by-two table [Figure 5].

Figure 5 A product table for the sum 65 × 115.

We then tried the other multiplication problems. They worked on this mainly on their own, although every now and then I could see students looking at their neighbour’s work. They could do most of them well. With the decimal question, most of them distributed it as 14 + 0.3. I asked them if they felt it was now simpler and some of them said that it was not, so I told them that they could think of a further decomposition to make a three-by-three table.

When they came to 982, the ones who decided on 90 + 8 had no problems, but one of them decided to represent it as 100 - 2 so then he wanted to know how an area could be negative. This led to a lively discussion about representation and modelling in mathematics and why it can be helpful to come up with different labels. In this case, the difference and sameness between a product table and an area representation. We conjectured that the product table and the area representation would be identical when working with positive numbers, but you would have problems with negative numbers in the area model because a negative area does not actually exist. However, we know a product can be negative, so that is why we would call it a product table!

I did not go deeper into the 100 - 2 representation itself, but it led nicely into discussing the next part of this unit: how to deal with negative numbers in a product table.

Pause for thought

Good questions to think about after the lesson are:

  • How did it go with your class?
  • What responses from students were unexpected? Why?
  • What questions did you use to probe your students’ understanding?
  • Did you feel you had to intervene at any point?
  • What points did you feel you had to reinforce?
  • Did you modify the task in any way? If so, what was your reasoning for this?

3 Algebraic identities seen as special cases of multiplication

Students often perceive algebraic identities as some magic or a gospel truth. They rarely develop a sense of where these identities appear from or that they are special cases of multiplication.

One of the reasons why students tend to memorise identities is that they fail to associate any meaning with the relationship being depicted by the identity. You may have noticed students making common errors when they recall identities such as:

left parenthesis equation left hand side x minus y right parenthesis squared equals right hand side x squared minus y squared
equation left hand side open x minus y close squared equals right hand side sum with, 3 , summands x squared plus two times x times y plus y squared
equation left hand side open x minus y close squared equals right hand side x squared plus two times x times y minus y squared

Even though it is fairly simple to check if the two statements are correct (all that is needed is to verify them for a few values of the variables), students continue to make these mistakes. Sometimes students are not aware of how easily they can verify their statements. Another and more serious reason is that they have never understood the physical (or geometric) meaning of these statements.

You can use the visualisation techniques you introduced in the previous section to help your students to understand these identities. Activity 2 gives you a method to help your students discover for themselves the meaning of different identities. The task focuses on finding, seeing and generalising the patterns of algebraic identities. Students work with a partner, as talking about the ideas helps to develop their understanding.

Before beginning this activity, it would be a good idea to first check your students can illustrate the lengths x + y and x - y correctly. The former is easier to conceive and the latter may take a bit more effort.

Illustrating the length ‘x + y’

If the white portion is x, and the grey portion is y, then the black portion is x + y. This could also be described as ‘the length of the white portion (representing x) added to the length of the grey portion (representing y) is the same as the black portion (representing x + y’ (see Figure 6).

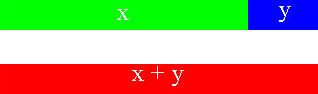
Figure 6 Illustrating the length x + y.

Illustrating the length ‘x – y’

If the white portion is x, and the grey portion is y, then the black portion is x - y. This could also be described as ‘the length of the white portion (representing x) take away the length of the grey portion (representing y) leaves the black portion (representing x - y)’ (see Figure 7).

Figure 7 Illustrating the length x - y.

Activity 2: Algebraic identities as special cases of algebraic multiplications

Tell your students the following:

  1. Describe (not draw or work out) the following mathematical expressions as a product table to your neighbour. What would it look like?
    • a.(x + y)2
    • b.(x + a)(x + b)
    • c.(x − y)2
    • d.(x − y)(x + y)
  2. Now draw the representation of each expression as you have described it in Step 1 as a product table.
  3. Try to write the mathematical expression that represents the areas you have drawn in Step 2 in a different way.
  4. Observe and compare your answers to Steps 1, 2 and 3 for each of the following four expressions:
    • How many terms do you get for the expressions (a), (b), (c) and (d) in Step 3?
    • How are these terms formed?
    • What is the same about these expressions? What is different? It might help if you colour in the area boxes corresponding to the terms.
    • Describe a rule or method for working out the algebraic identities in this way so other students in other classes could read about it.

Case Study 2: Mrs Kapur reflects on using Activity 2

Because I thought there would be some students who would find moving from number to algebra confusing, we did the first question, (x + y)2, as a whole class activity. Because of this, and because the students had already made product tables in Activity 1, the students could do Steps 1 and 2 fairly easily.

Step 3 led to a discussion about the significance of equivalence. An expression with collected terms can be equivalent to one where the terms have not been collected yet – it just looks a bit messier somehow! I asked them whether they could come up with some ideas to make it look even more messy, and they had great ideas! It made us all laugh, which was really nice, especially as the students who are normally very quiet and perhaps have some mathematics anxiety also smiled and looked more relaxed.

The last part of Step 4 proved hard. The difficulty was not in describing it, but in doing so succinctly. The descriptions we ended up with were not perfect, but the students and I were happy with them. We all realised that to improve we would simply need more practice at writing our own descriptions and methods.

We extended the questions to include (a + b + c)2 and then tried with terms being assigned different signs, and they could get the solutions easily.

We also decided that to do (a + b)3 or (a − b)3, we could do it in two parts, (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2), and then put this in the product table.

The students felt really happy and confident with working in this way. One student said that he felt so relieved that he would now be able to think of a way to work out the algebraic identities if his memory failed.

Pause for thought

Good questions to think about after the lesson are:

  • How did it go with your class?
  • Did all the students participate? Or did you notice any students who were not engaged in the task? How could you engage them in the next lesson?
  • What responses from students were unexpected? Why?
  • What questions did you use to probe your students’ understanding?
  • Did you modify the task in any way? If so, what was your reasoning for this?

4 Spotting patterns and adjusting algebraic identities

In Activity 2, you worked with your students on developing an image of multiplication and algebraic identities. Your students will now be aware of methods other than memorising formulae and algorithms to work out the products of multiplication and algebraic identities.

The power of understanding algebraic identities in mathematics is not only in being able to work out their products, but also (and perhaps more importantly) in being able to spot them when they are not in an easily recognisable form. To be able to ‘tweak’ expressions so they can be written as variations of algebraic identities is also a very powerful skill to have.

Activity 3 focuses on this. It requires students to actively develop ways to spot patterns and manipulate expressions in the context of algebraic identities.

Activity 3: Spotting patterns

This is an activity about spotting patterns and manipulating mathematical expressions in the context of algebraic identities.

Ask your students to decide whether each of the calculations below is an example of an ‘algebraic identity’. They can find these in their textbook:

  • 5.62 − 0.32 = 31.27
  • (x − 3)(x + 5) = x2 + 2x – 15
  • 118 × 123 = 14514
  • 25/4x2 – y2/9 = (5/2x + y/3)(5/2x – y/3)

Case Study 3: Mrs Agarwal reflects on using Activity 3

I told the students to look up the algebraic activities to remind themselves what these are. After that, the students happily started comparing the given questions with the identities. For the first one, they did identify the correct identity, but Suman and a few others wrote it as 5.62 − 0.32 = (5.62 − 0.32)(5.62 + 0.32). I thought her error might be good to share with other students so they could all learn from her mistake. So I asked her to come to the blackboard and write it down. At once, Ravi asked ‘How can it be that on the right-hand side [RHS] we have the same expression, but then it is multiplied by another?’ Suman immediately saw what she had done and rubbed out the indices on the RHS, leaving the correct answer.

The second one was done easily enough, but for the third, some distributed it as 100 + 18 and 100 + 23. This led to a discussion on whether that was simplified enough or if there another way of making it simpler. I liked that the students were actually thinking about different ways to get to an answer.

Some of the students wanted to write the last one as open five times times times four x minus y times nine close times open five times times times four x plus y times nine close . There was a lot of discussion on what was right and wrong with this suggestion. Then I asked them to take out their textbook, not to ‘do the exercise’, but to now see if they could easily identify the identities that they needed to use.

Video: Assessing progress and performance

You may also want to have a look at the key resource ‘Assessing progress and performance’.

Pause for thought

Good questions to think about after the lesson are:

  • What responses from students were unexpected? Why?
  • What questions did you use to evaluate your students’ understanding?
  • Did you modify the task in any way? If so, what was your reasoning for this?

5 Summary

This unit has focused on using visual representations to facilitate working with complex expressions. Once your students grasp the connections between area calculations and expanding brackets, they immediately have a way of working out identities rather than relying on their memories. These ideas allow students to give a meaning to what they are doing and therefore to feel that the ideas are their own.

It also suggests that the students play with these ideas, asking ‘What if I do it this way instead of that way, or make it more messy rather than less?’ This can relieve some of the anxieties from demanding memorisation and help students to remember what they learned more easily. This is important, because when students can reproduce identities from memory, they can solve mathematical problems more fluently. But often they are so worried about memorising, they cannot develop the fluency.

Pause for thought

Identify three ideas that you have used in this unit that would work when teaching other topics. Make a note of two topics you have to teach soon where those ideas can be used with some small adjustments.

Resources

Resource 1: NCF/NCFTE teaching requirements

This unit links to the folllowing teaching requirements of the NCF (2005) and NCFTE (2009) and will help you to meet those requirements:

  • Let students see mathematics as more than formulae and mechanical procedures.
  • View learners as active participants in their own learning and not as mere recipients of knowledge; encouraging their capacity to construct knowledge; shifting learning away from rote methods.
  • Engage with the curriculum, syllabuses and textbooks to critically examine them rather than taking them as ‘given’ and accepted without question.
  • Let students use abstractions to perceive relationships, to see structures, to reason out problems, to argue the truth or falsity of statements.

Additional resources

References

De Morgan, A. (1865) ‘A speech of Professor De Morgan, President, at the first meeting of the London Mathematical Society’, Proceedings of the London Mathematical Society, Vol.1 (1866), pp. 1–9.
Dörfler, W. (1991) ‘Meaning: image schemata and protocols – plenary lecture’, in Furinghetti, F. (ed.) Proceedings of PME XV, Vol. I, pp. 95–126.
Marton, F. and Booth, S. (1997) Learning and Awareness. Mahwah, NJ: Erlbaum.
National Council of Educational Research and Training (2005) National Curriculum Framework (NCF). New Delhi: NCERT.
National Council of Educational Research and Training (2009) National Curriculum Framework for Teacher Education (NCFTE). New Delhi: NCERT.
National Council of Educational Research and Training (2012a) Mathematics Textbook for Class IX. New Delhi: NCERT.
National Council of Educational Research and Training (2012b) Mathematics Textbook for Class X. New Delhi: NCERT.
Skemp, R. (1976) ‘Relational understanding and instrumental understanding’, Mathematics Teaching, vol. 77, pp. 20–26.
Van Hiele, P. (1986) Structure and Insight: A Theory of Mathematics Education. Orlando, FL: Academic Press.
Watson, A., Jones, K. and Pratt, D. (2013) Key Ideas in Teaching Mathematics. Oxford: Oxford University Press.

Acknowledgements

This content is made available under a Creative Commons Attribution-ShareAlike licence (http://creativecommons.org/ licenses/ by-sa/ 3.0/), unless identified otherwise. The licence excludes the use of the TESS-India, OU and UKAID logos, which may only be used unadapted within the TESS-India project.

Every effort has been made to contact copyright owners. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.

Video (including video stills): thanks are extended to the teacher educators, headteachers, teachers and students across India who worked with The Open University in the productions.

 TI-AIE: Using visualisation: algebraic identities

Copyright © 200X, 200Y The Open University