Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Saturday, 22 November 2025, 3:31 PM
TI-AIE: Building mathematical resilience: similarity and congruency in triangles
What this unit is about
All learning requires a certain amount of resilience, and it is widely recognised that pupils in school today will need the resilience to learn throughout their lives. Mathematics seems to require a particular kind of resilience; partly because of the way that it is viewed in society, but also because many people require perseverance and effort to keep trying to overcome barriers that arise because of the way that mathematics is often presented. Helping students to build the kinds of resilience can enable them to learn mathematics better will, in turn, ensure that they get the qualifications that will maximise their life chances.
A good example of the complexity of mathematics can be found in the congruency and similarity of triangles, which is what you will study in this unit. These are in essence very simple and straightforward concepts; but look in any textbook and notice the inventiveness and creativity of mathematicians who, over the centuries, have developed so many mathematical ideas from such straightforward concepts.
Through the activities in this unit, you will also help to develop your students’ resilience in learning mathematics in order to feed their curiosity and ability to explore mathematical ideas – and as a result, put in the sufficient effort and perseverance to be successful.
What you can learn in this unit
- How to build students’ resilience when learning mathematics.
- Some suggestions to help your students to become better at learning mathematics.
- Some ideas on how to engage students in anticipating and overcoming difficulties when learning mathematics.
This unit links to the teaching requirements of the NCF (2005) and NCFTE (2009) outlined in Resource 1.
1 Resilience and mathematical resilience in learning
Pause for thought Working with triangles is an important part of the syllabus in the Indian curriculum. You can find it in the textbooks for Class IX and Class X where triangles, congruency and similarity are addressed. (In the NCERT books, chapters 7 and 8 for Class IX, and chapters 6, 11 and 13 for Class X.) Why do you think it is studied so often? Do you agree with its emphasis in the curriculum? |
Resilience is the ability to cope with problems and setbacks; to keep going even when the going is tough. We all need to be resilient to some extent to function well in life.
Current educational practice and research focuses on the importance of being resilient in learning and the effect of resilience on academic achievement and professional success. Lifelong learning is becoming the norm in society. Resilient learners will have a positive stance towards learning and will continue with their learning even when there are problems and obstacles, which can range from home issues such as not being able to find a quiet place to work or feeling hungry, to learning issues such as not being able to make sense of mathematical formulae.
Having mathematical resilience is particularly important. Lee and Johnston-Wilder (2013) describe mathematical resilience as ‘a learner’s stance towards mathematics that enables pupils to continue learning despite finding setbacks and challenges in their mathematical learning journey’. They argue that ‘pupils require a particular resilience’ in order to learn mathematics because of various factors that include:
- the types of teaching often involved (Nardi and Steward, 2003)
- the nature of mathematics itself (Mason, 1988)
- pervasive beliefs about mathematical ability being ‘fixed’ (Dweck, 2000).
Pause for thought Think back to when you last worked on mathematics yourself. Would you describe yourself as a mathematically resilient learner? Why is that? What do you do in your learning that makes you consider yourself a mathematically resilient learner or otherwise? Think about some students in your classroom and how they deal with learning mathematics. Think of one particular student that you consider mathematically resilient, and one that is not. What is the same and what is different in their learning behaviour? |
2 Teaching for mathematical resilience
Developing a ‘growth mindset’ about learning mathematics
Students who have developed ways to work on mathematical problems that allow them to continue, even when they encounter problems, can be said to be mathematically resilient. Such students will have a ‘growth mindset’ (Dweck, 2000), which means that they know that the more they work to overcome challenges and solve problems, the ‘smarter’ they will become. Students with a growth mindset do not accept that they have any ceiling or limit on what they can learn. Hence, they will discuss and question mathematical ideas with anyone who may help them, until they have fully grasped the ideas. Working in this resilient way demands sufficient mathematical vocabulary to explain ideas and to work collaboratively.
Experimenting and questioning are part of being mathematically resilient. Students who are encouraged to ‘play with mathematical ideas’, for example by using ICT tools or manipulatives, develop their resilience because they see that they can explore and start to understand those ideas. Working collaboratively is another important way to develop resilience, as students can receive help from their peers as and when they need it. A resilient student will seek help from a variety of sources: older students, textbooks, the internet, teachers, a clever uncle, etc.
Another important aspect in developing students’ resilience is to enable them to see asking questions as ‘clever’ and to see persistent asking as being ‘even cleverer’. All students have to know that the only one who can take responsibility for their learning is themselves and therefore they have to actively seek understanding. The mathematically resilient student will have a good understanding of their own strengths and will know how to get appropriate help to improve any limitations.
In short, mathematically resilient pupils will assert, in their practice, their right not to be mathematically isolated or feel mathematically stupid; they will resist any expectation that they should passively accept mathematical ideas but they will demand to be allowed to work at understanding them for themselves. They will reclaim their right to progress their own mathematical thinking, using existing knowledge, skills, understanding and strategies, and be confident about their ability to learn new mathematics.
(Lee and Johnston-Wilder, 2013)
Working in ways that develop mathematical resilience
According to Lee and Johnston-Wilder (2013), in order to develop mathematical resilience, students must have the opportunity to do the following:
- Learn sufficient mathematical vocabulary and ways of expression to engage in mathematical conversations, question concepts, work collaboratively, think mathematically and build understanding. This means that pupils have to use mathematical words and ways of expression for themselves, and not only listen to their teachers using the mathematical language.
- Make mistakes and take wrong turns, so that ultimately develop the belief that if they persevere they will be far more likely to succeed.
- Extend their ability to experiment and try out ideas in a mathematical environment and, in our experience, discover that they enjoy it.
- Seek solutions to significant problems. Working on such problems will require pupils to try things out, to make and recognise mistakes for themselves and work for an extended time with other people to produce a well-reasoned solution.
- Acquire a reflective and thoughtful stance towards mathematics. They will know that, if they think hard, talk to others, read about mathematical ideas and reflect on the information gained, they will be able to make headway with seemingly difficult ideas and problems.
The activities in this unit will work on developing these five resilient skills.
3 Developing mathematical language
Becoming mathematically resilient requires students to notice what they are struggling with and to express their questions, thoughts and ideas. To be able to do so, students need to have the opportunity to learn to read, interpret and apply mathematical vocabulary. As with learning any language, this involves identifying words and expressions, using them in different contexts and phrases, and giving meaning to the words and expressions. To learn a language effectively you need to regularly hear it, see it, read it, write it and get practice at speaking it.
Activity 1 explores how to deal with mathematical vocabulary. It requires students to devise their own mathematical dictionary, identify mathematical words and statements that need clarification, write their own explanations and sound these out with another student. In doing this they will also learn how to make sense of mathematical language for themselves, which can also help them get ‘unstuck’ when learning mathematics.
The mathematical context of all the activities in this unit is triangles, and in particular, the similarity and congruence of triangles. However, the approaches taken in the activities can be applied for all topics the students study.
In Part 3 of Activity 1, students are also asked to reflect on their learning in Parts 1 and 2. This is repeated in most of the activities in this unit. The purpose of this is for students to become more aware of what works for them when learning, and become more active in their learning as a result.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, as that will help you when you reflect on the experience. Trying the activities yourself will mean that you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, use the activities with your students. After the lesson, think about the way that the activity went and the learning that happened. This will help you to develop a more learner-focused teaching environment.
Activity 1: Making your own mathematical dictionary
This activity requires students to exchange their ideas with other students – they could be working in pairs or small groups to prompt more ideas and responses. Think about timing for the activity so that it does not overrun and all parts are addressed; for example, say, ‘In the next ten minutes I want you to find as many …’
You can find some examples of entries in a student’s dictionary in. Resource 2.
Part 1: Making the dictionary
Tell your students the following:
Look at the chapters in your textbook about triangles.
- Write down a list of geometric words that are being used.
- On your list, are there any words that are also used in everyday life? What is the same and what is different between the geometric meaning and the everyday meaning?
- Write down your own explanation of the geometric words. It might help to add a sketch or drawing as well.
Part 2: Giving meaning to mathematical statements
Tell your students the following:
Again, in groups or pairs, look at the chapters in your textbook about triangles.
- Write down any mathematical statements you come across that students might find difficult to understand. For example: ‘two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle (SAS congruence rule)’.
- Identify the words that do not make sense for you in the context of the statement. From the example above, this could be the word ‘included’, which you might understand in everyday language but might find hard to explain in the mathematical statement.
- Discuss and write down what the meaning of these words could be. Try and be as precise as you can.
For this part of the activity it might be helpful to have some examples ready rather than getting the students to find them. You can take them from the text that they are looking through. This will save time as they do not need to search for examples.
Part 3: Reflecting on your learning
Tell your students the following:
This part of the activity wants you to think about your learning so you can become better at, and feel more comfortable, learning mathematics.
- What did you find easy or difficult about Part 1 of this activity?
- What did you like about this activity?
- What mathematics did you learn from this activity?
- What did you learn about how you (could) learn mathematics?
You may also want to have a look at the key resources ‘Using local resources’ and ‘Using groupwork’.
Case Study 1: Mr Agarwal reflects on using Activity 1
This is the account of a teacher who tried Activity 1 with his secondary students. He teaches in an English-medium school.
The students were quite happy starting on this activity; they opened their books and looked for words they felt were new to them or typical to geometry.
As I walked around the classroom, I noticed they found out from each other or from reading the explanations in the textbook the meanings of some of the words, and leaving blanks for the ones they did not know. There was actually much noise from students asking each other what the words might mean. Perhaps next time I would say they are only allowed to ask the students sitting next to them, not in front or behind. On the other hand, the noise was mathematical talk and they did find out more by being able to ask more people.
After a while, I reminded them they also had to do the other questions in the activity, which were to attempt to write it down in their own words, make a sketch and then think and write down whether they had seen that word in any other context than mathematics, and what it would mean there. The students found the last question about meaning hard: their use of the English language is not extensive and I encouraged them to look for the meaning in the dictionary so that they could see how closely related, or not, the everyday word was to the mathematical word. For some of the students I needed to translate the words into Hindi.
It was an extremely productive exercise for both the students and me: the students had an opportunity to really work on the language aspect of mathematics, in writing, reading and verbalising it. For me, it made me realise to what extent the language used in mathematics is alien to the students and a barrier to their learning of mathematical ideas. I really want to spend more time and attention on the language learning of mathematics in the future – if the words have no meaning for them, then how can they learn about them? For example, I have started compiling a mathematical English–Hindi dictionary that we have available in the classroom.
Reflecting on your teaching practice
When you do such an activity with your class, reflect afterwards on what went well and what went less well. Consider the questions that led to the students being interested and being able to get on, and those you needed to clarify. Such reflection always helps with finding a ‘script’ that helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved. Use this reflective exercise every time you undertake the activities, noting, as Mrs Agarwal did, some quite small things that made a difference.
Pause for thought Good questions to trigger such reflection are:
|
4 Dealing with misconceptions and mistakes
When you learn to ride a bicycle you have to learn to gain balance. It is accepted that in that process of learning to ride a bike you will fall off a couple of times, make the wrong movements, pull the handlebar too briskly, forget where the brakes are, or have the wrong idea about how gears work. It is only by making mistakes like these that you will develop and refine your cycle skills. Making mistakes and being confronted with your misconceptions makes you learn better in the future.
Learning mathematics is no different from learning to ride a bike or anything else. Making mistakes is part of that process, and is actually a good thing, because it interferes with your routine thinking patterns and makes you reflect on what you are doing. If there is a classroom ethos that learning happens from making mistakes, and hence, making mistakes is part of effective learning, then students will also become more willing and more able to experiment and try out new ideas, less afraid of getting it wrong, and consequently be better equipped to explore and enjoy mathematics.
Establishing such a classroom ethos where students are willing to share their mistakes and misconceptions does not happen overnight – it requires nurturing and careful coaching. However, there are methods you can use to promote this ethos:
- Use work from fictitious students to expose possible misconceptions. Because it is not their own work that is being scrutinised, there are no emotional reactions and/or feelings of embarrassment.
- Encourage reflection on mistakes and misconceptions rather than dismissing an answer as simply ‘wrong’ – this provides a fruitful way for learning.
- Promote sharing of ideas, even if they are half formed or ‘wrong’.
The next activity is designed so that it is very likely students will make mistakes. Discussing these explicitly will help elicit misconceptions and turn these into opportunities for learning mathematics.
Activity 2: Triangles challenge – learning from misconceptions and mistakes
Part 1: Playing the triangle challenge
Divide your class into groups of three students.
Explain the following to your students:
- One student in each group, the leader, has to draw a triangle, without showing the triangle to the other two students. The leader describes their triangle, one fact at a time. The other two students each need to draw the same triangle from the facts that the leader gives. They have to concentrate on getting the size and shape right.
- If the two students cannot complete their triangles using the facts shared with them, they say, ‘Tell me more’. The leader then reveals another fact about their triangle. After the two students have drawn their triangles, the leader gives them one point if their triangle is the same; otherwise they get no points. The original triangle and the ones that get awarded a point are kept in a class pile of triangles. The others are discarded.
- The group repeats the activity two more times, with other students taking turns as leaders.
After they have done the activity above, ask the students the following questions:
- Which triangle was easier to make? Why?
- Why did some of you not get a congruent triangle while others did? What mistakes were made and why?
Part 2: Continuing the challenge
Explain to your students that the class pile of triangles created in Part 1 now becomes the focus. Each group of three collects one triangle from the pile. One student volunteer picks one of the remaining triangles at random from the pile and then describes it to the class one fact at a time. Students check their triangles in their groups to determine if they have an ‘exact match’ or a ‘similar match’. Again, an exact match gets a point.
Repeat this exercise until all the remaining triangles have been used up.
After each round, answer the following questions:
- After how many facts was a match found?
- Could you have gotten a match with fewer facts?
- Did you find an ‘exact’ match or a ‘similar’ match?
- Why do you think this is so?
Part 3: Reflecting on your learning
This part of the activity asks the students to think about their learning so that they can become better at and feel more comfortable about learning mathematics. Ask your students the following.
- What did you find easy or difficult about Part 1 of this activity?
- What did you like about the activity?
- What mathematics did you learn from?
- What did you learn about how you (could) learn mathematics?
Case Study 2: Mrs Nagaraju reflects on using Activity 2
I distributed pieces of paper to the groups for writing down their answers. I then explained the activity to them. I modified the activity slightly by asking them to also write down the facts given by the leader that they used to draw their triangle and told them this would help them to see why they could draw a triangle and in just how many steps.
The students were very excited about doing this activity. They seemed to like the sense of competitiveness and also that they had a chance of all being the leader. There were some complaints about how one student had cheated and been given an extra point. I told them that it was a discredit to them if they cheated and they would have to explain how they had got to where they were anyway.
The discussion about learning from mistakes was interesting. I had expected the students to be reluctant to talk about their mistakes but I was wrong – they talked about them with gusto! Perhaps it was because they were able to talk about them in groups first, which was less threatening. I then asked the students to share their mistakes with the whole class, and wrote them on the blackboard. We discussed these in terms of: ‘This is interesting. Why would this mistake have been made? What were they thinking?’ All the students in the class learned much from these misconceptions. We also discussed whether we did learn from making and discussing these mistakes – and we all agreed that we did. Some students mentioned that they had now finally discovered that they had a misconception. Others who did ‘get it right’ from the start said it was good to hear and find out why it was they were thinking correctly because often they just did the activities and questions without thinking.
Pause for thought
|
5 Summary
This unit has focused on similarity and congruence in triangles, and on developing mathematically resilient learners who develop a positive stance towards mathematics and know they can overcome difficulties they encounter in learning the subject. In reading this unit you will have thought about how to enable your students to develop their vocabulary so that they can talk about their ideas and explain their conceptions (and their misconceptions) to other students and adults alike. You will also have considered how to help your students to understand that making mistakes is a vital part of learning, and that exploring and persevering are important skills to acquire if they are to be successful learners of mathematics.
You will have also seen how reflecting on the learning process is important in becoming better at learning in general. Mathematically resilient learners are much more likely to succeed in examinations because they are not discouraged by difficulties, but rather seek ways to overcome them, and will have the tools they need to carry on using mathematical ideas in their lives beyond school.
Pause for thought Identify three ideas that you have used in this unit that would work when teaching other topics. Make a note now of two topics you have to teach soon where those ideas can be used with some small adjustments. |
Resources
Resource 1: NCF/NCFTE teaching requirements
This unit links to the following teaching requirements of the NCF (2005) and NCFTE (2009) and will help you to meet those requirements:
- View learners as active participants in their own learning and not as mere recipients of knowledge; how to encourage their capacity to construct knowledge; how to shift learning away from rote methods.
- Let students see mathematics as something to talk about, to communicate through, to discuss among themselves, to work together on.
- Engage with the curriculum, syllabuses and textbooks critically by examining them rather than taking them as ‘given’ and accepted without question.
- Let students learn important mathematics and see mathematics is more than formulas and mechanical procedures.
Resource 2: Examples of entries of a student’s mathematical dictionary
| Word/concept | Congruence in triangles |
| Where? | Chapter 7, Class IX |
| Any meaning in everyday language? | According to the dictionary, ‘congruent with’ means ‘suitable, agreeing’, but I have never used that or heard that (The Oxford Dictionary, 1997). |
| Mathematical explanation from textbook/teacher | ‘Equal in all respects’ or ‘figures [triangles in this case] whose shapes and sizes are both the same’ (NCRT textbook, Class IX, p. 109). |
| My explanation | Congruent triangles are triangles that are identical in shape and size. Sometimes I have to turn them around or flip them over to actually see this. So the lengths of their sides and the angles will be the same for the congruent triangles. But not only that! Those same length sides and angles have to be in the same place in the triangle – that is what they call ‘corresponding’. When you cut out the triangles, you can place them on top of each other and they will be perfect copies. Congruent triangles are at the same time similar triangles, but similar triangles are not always congruent! Also, have a look at my entry for ‘similar triangles’ to see how these concepts are connected. |
| Illustration | These triangles are congruent: |
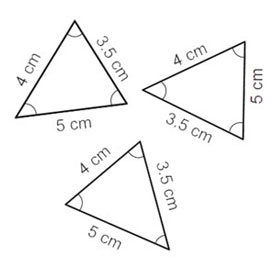 | |
| Word/concept | Similarity of triangles |
| Where? | Chapter 6, Class X |
| Any meaning in everyday language? | Something that is like something else. What makes something like something else is often not made clear. |
| Mathematical explanation from textbook/teacher | ‘Two triangles are similar, if
(NCRT textbook, Class X, p. 123) |
| My explanation | Note to myself: do not mix up with congruent! Similar triangles have the same shape but not necessarily the same size. If they do have the same shape and the same size they are similar as well as congruent. So they have to be similar in shape, but not identical in size. What makes them similar is that the shapes are a proportional enlargement or reduction of each other. That means that the proportion or ratio of all the corresponding sides will be the same (for example, the second triangle has sides twice the size of the first). And that is why these criteria about similarity of triangles make sense. |
| Illustration | These triangles are similar: |
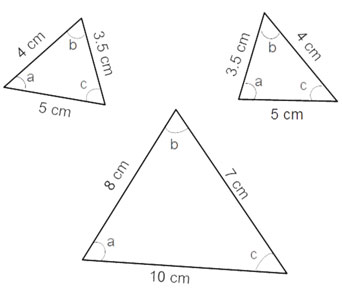 |
Additional resources
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- Class X maths study material: http://www.zietmysore.org/ stud_mats/ X/ maths.pdf
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- OpenLearn: http://www.open.edu/ openlearn/
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Mathcelebration: http://www.mathcelebration.com/
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Maths is Fun: http://www.mathsisfun.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Central Board of Secondary Education’s books and support material (also including the Teachers Manual for Formative Assessment – Mathematics (Class IX)) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
This content is made available under a Creative Commons Attribution-ShareAlike licence (http://creativecommons.org/ licenses/ by-sa/ 3.0/), unless identified otherwise. The licence excludes the use of the TESS-India, OU and UKAID logos, which may only be used unadapted within the TESS-India project.
Every effort has been made to contact copyright owners. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Video (including video stills): thanks are extended to the teacher educators, headteachers, teachers and students across India who worked with The Open University in the productions.