Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Saturday, 27 April 2024, 5:53 AM
गणितीय ढंग से सोचनाः अनुमान लगाना
यह इकाई किस बारे में है
अनुमान लगाना हमारे दैनिक जीवन का एक अनिवार्य हिस्सा है, क्योंकि ज्यादातर संदर्भों में, हम किसी माप के वास्तविक मान की अपेक्षा एक अनुमान के प्रति ज्यादा चिंतित होते हैं। उदाहरण के लिए, यदि हमें स्थान A से स्थान B जाना होता है, हमारी रुचि यात्रा पूरी होने में लगने वाले वास्तविक समय की अपेक्षा यात्रा की अवधि का अनुमान लगाने में रहती है।
समान मात्रा का अनुमान लगाने के लिए किए गए दोबारा प्रयास हमारे अनुमान को बेहतर बनाते हैं। उदाहरण के लिए, एक फल के जूस का विक्रेता (चित्र 1), अपने अनुभव से, बहुत सटीक तरीके से यह अनुमान लगा सकता है कि पांच गिलास जूस कितने संतरों से निकाला जा सकता है।

फिर भी, विद्यार्थी अक्सर ही अनुमान लगाने की प्रक्रिया पर ध्यान नहीं देते और इसकी बजाय सटीक उत्तर प्राप्त करने का प्रयास करते हैं–– तब भी जब उनसे खास तौर पर ऐसा नहीं करने को कहा गया हो। क्योंकि वे आत्मविश्वासी अनुमानकर्ता नहीं होते, उनके पास ऐसे उपकरण नहीं होते, जो उन्हें इस बात को महसूस करने में मदद करें कि कब उनके सुविचारित उत्तर विश्वसनीय नहीं होते।
इस इकाई में आप इस बात पर ध्यान केन्द्रित करेंगे कि गणितीय सोच पर काम करने और गणितीय गणनाओं में न्यूनतम त्रुटियां करने के लिए एक उपकरण के रूप में अनुमान लगाना कैसे सिखाएं। इन गतिविधियों में आपके विद्यार्थियों से कहा जाएगा कि वे अपने गणित संबंधी सोच प्रक्रियाओं पर काम करें और विचार–विमर्श के द्वारा इन्हें स्पष्ट करें।
आप इस इकाई में क्या सीख सकते हैं
- संख्यात्मक अभिव्यक्तियों, लंबाई, समय और क्षेत्रफल के मानों का अनुमान लगाने और ऊपरी और निचली सीमाओं का उपयोग करने की विद्यार्थियों की क्षमता को कैसे बढ़ाएँ।
- आपके विद्यार्थियों को किस प्रकार सक्षम करें कि वह गणित को केवल एक सही उत्तर वाला नहीं, बल्कि ‘कई सही उत्तर’ वाले के रूप में देखें
- विद्यार्थियों की सोच प्रक्रियाओं को शामिल करने की कुछ पद्धतियाँ।
इस यूनिट में शिक्षण का संबंध संसाधन 1 में निर्दिष्ट की गई एनसीएफटीई (2005, 2009) शिक्षण आवश्यकताओं से है।
1 अनुमान लगाना गणितीय प्रक्रिया के बारे में सोचना है
जीवन में ज्यादातर चीज़ों की तरह, और खास तौर पर फल जूस के विक्रेता की तरह, आप अनुमान लगाने का जितना ज्यादा अभ्यास करते हैं, इस पर काम करते समय आपको उतना ही बेहतर परिणाम प्राप्त होता है। मजेदार प्रश्न यह है कि एक अच्छा अनुमानकर्ता होना एक अच्छा विचार क्यों है? आप अपने विद्यार्थियों को अच्छे अनुमानकर्ता बनने के लिए प्रोत्साहित करना क्यों चाहते हैं? अनुमान लगाने से ऐसी कौन सी शिक्षा मिलती है, जो सटीक उत्तर पर काम करने से भिन्न है?
अनुमान करते समय, विद्यार्थी अपने सामने मौजूद समस्या को हल करने के लिए आवश्यक सोच प्रक्रिया पर वास्तव में विचार करना शुरू कर सकते हैं, इन बातों के दबाव के बिना कि उन्हें एकदम सही उत्तर प्राप्त करना है, और उन्हें सही गणनाओं के विस्तार में जाना है। कलन विधि लागू करने से सटीक उत्तर प्राप्त होगा, अनुमान नहीं। इसलिए, अनुमान लगाना उस सोच की रूपरेखा बनाना है, जो विकसित होगी, साथ ही उन क्षेत्रों का बोध होना है, जहां समस्या का समाधान हो सकता है। यह विद्यार्थियों को सोचने के लिए विवश कर सकता है कि कलन विधि क्यों काम करती है। जब बाद में वे किसी प्रश्न का सही उत्तर निकाल लेते हैं, तो वे इस बात की पुष्टि कर सकते हैं कि अनुमान लगाने की प्रक्रिया में उनकी सोच स्पष्ट थी या नहीं, और इस तरह उन्हें गणनाओं के करने में की गयी किसी भी त्रुटि के बारे में पता चलता है।
तो इस प्रकार, अनुमान करना गणितीय सोच के लिए एक उपकरण है। यह खास तौर पर भारत में प्रासंगिक है, क्योंकि स्कूल की गणित में कैलकुलेटर्स के प्रयोग की अनुमति नहीं है – इसलिए लम्बी गणनाओं में फंसना एक वास्तविकता है।
गतिविधि 1 में आप अपने विद्यार्थियों से कहेंगे कि पहले वे प्रश्नों में अनुमान लगाने का अभ्यास करें, जिसका उन्होंने ज्यादा प्रयोग किया हो, लेकिन यह गतिविधि उन्हें इस बात के लिए भी बाध्य करेगी कि वे तमाम संभावित उत्तरों के बारे में भी सोचना शुरू करें। गतिविधि के प्रश्न 3 में आप उनसे कहेंगे कि वे वास्तविक जीवन की किसी वस्तु का उपयोग करते हुए की जाने वाली गणनाओं में शामिल गणितीय सोच प्रक्रिया का वर्णन करने के एक तरीके के तौर पर अनुमान करने के बारे में सोचें।
इस यूनिट में अपने विद्यार्थियों के साथ गतिविधियों के उपयोग का प्रयास करने के पहले अच्छा होगा कि आप सभी गतिविधियों को पूरी तरह (या आंशिक रूप से) स्वयं करके देखें। यह और भी बेहतर होगा यदि आप इसका प्रयास अपने किसी सहयोगी के साथ करें, क्योंकि जब आप अनुभव पर विचार करेंगे तो आपको मदद मिलेगी। स्वयं प्रयास करने से आपको शिक्षार्थी के अनुभवों के भीतर झांकने का मौका मिलेगा, जो परोक्ष रूप से आपके शिक्षण और एक शिक्षक के रूप में आपके अनुभवों को प्रभावित करेगा। जब आप तैयार हों, तो अपने विद्यार्थियों के साथ गतिविधियों का उपयोग करें। पाठ के बाद, सोचें कि गतिविधि किस तरह हुई और उससे क्या सीख मिली। इससे आपको अधिक विद्यार्थी–केंद्रित रखने वाला शैक्षिक वातावरण बनाने में मदद मिलेगी।
गतिविधि 1: अनुमान लगाना और त्रुटियां करना
अपने विद्यार्थियों से निम्नलिखित पूछें:
- सटीक उत्तर की गणना किए बिना दी गयी सांख्यिकीय अभिव्यक्तियों के निकटतम पूर्णांक का पता लगाएं।
- a.

- b.
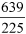
- c.
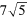
- a.
- चर राशियों के दिए गए मूल्यों पर इन अभिव्यक्तियों के मूल्यों का अनुमान लगाएं। एक बार फिर, सटीक उत्तर की गणना नहीं करें।
- a.यदि हो तो के मूल्य का अनुमान लगाएं
- b.यदि हो तो के मूल्य का अनुमान लगाएं
- c.यदि हो तो के मूल्य का अनुमान लगाएं
- चित्र 2 में प्रदर्शित पारम्परिक चारपाई को बनाने में प्रयोग होने वाली रस्सी की लम्बाई का अनुमान लगाएं।

जब आपके ज्यादातर विद्यार्थियों ने प्रश्नों को हल करने का एक प्रयास कर लिया हो, तो उनसे पूछें:
- क्या आप बता सकते हैं कि इन प्रश्नों का जवाब देने के लिए आपने क्या किया? अनुमान लगाने की प्रक्रिया में आपको क्या करना अथवा सोचना पड़ा? प्रश्न 3 में आपने क्या किया इसपर पहले नजर डालना आपके लिए मददगार हो सकता है।
अनुमान लगाने में विद्यार्थी विभिन्न तरीकों का प्रयोग कर सकते हैं। उनके सभी सुझावों को स्वीकार करना महत्वपूर्ण है और तब उनसे अनुमान लगाने के विभिन्न तरीकों का मूल्यांकन करने को कहें।
केस स्टडी 1: गतिविधि 1 के उपयोग का अनुभव श्रीमती सोनिया बताती हैं
यह एक शिक्षिका की कहानी है, जिसने अपने माध्यमिक कक्षा के विद्यार्थियों के साथ गतिविधि 1 का प्रयास किया।
प्रश्न 1 और 2 को हमने पूरी कक्षा की गतिविधि के तौर पर किया। मैंने ब्लैक बोर्ड पर एक समय में एक प्रश्न लिखा, और तब विद्यार्थियों से उत्तर और विचार प्राप्त किया। प्रश्न 3 और 4 के लिए हमने पूरी कक्षा के तौर पर काम शुरू किया, और बाद में उन्होंने जोड़े बनाकर इसपर काम किया।
जब मैंने पहला प्रश्न ब्लैकबोर्ड पर लिखा, विद्यार्थी एक दूसरे की ओर बहुत संदेह भरी नजरों से देख रहे थे, जैसे उन्हें इससे पहले इस तरह की कोई चीज़ करने के लिए कभी भी प्रोत्साहित नहीं किया गया हो –– वे केवल सटीक उत्तर की गणना करना चाहते थे।
अचानक, रचित ने कहा कि यह 4,20,000 होगा। मैंने उससे पूछा कि उसने ऐसा क्यों सोचा और उसने कहा कि 6 बार 7 होता है 42 और सौ बार सौ के लिए हमने चार शून्य जोड़ दिए। साक्षी ने तुरंत कहा कि 6 और 7 इकाई वाले स्थान पर थे, इसलिए ऐसा नहीं होगा, लेकिन उसने कहा कि उसका सोंचना है कि यह 10,000 से ज्यादा होगा, क्योंकि 106 और 107 अंक 100 से बड़े हैं और 100 × 100 है, 10,000 के बराबर। तरुना और राहुल इससे सहमत थे।
प्रश्न 1 के भाग (b) ने उनकी गति थोड़ी धीमी कर दी, लेकिन तरुना ने फैसला किया कि यह 2 से ज्यादा और 3 से कम होगा। जब इसक पीछे का तर्क पूछा गया, उसने कहा कि 3 बार 225 होगा 675, जो अंश से अधिक है, और दो बार 225 होगा 450, जो अंश से कम है। भाग (c) के लिए, आदित्य ने फैसला किया कि यह 14 से ज्यादा होगा क्योंकि रूट 4 होता है 2, और इसलिए रूट 5 उससे ज्यादा होगा और इस प्रकार गुणन का परिणाम 14 से ज्यादा होगा।
उनके तर्क में मुझे यह बात खटकी कि उन्होंने ’इससे ज्यादा’ अथवा ’इससे कम’ की भाषा का इस्तेमाल स्वतः ही शुरू कर दिया। इससे लगता है कि ऊपरी और निचली सीमाओं के बारे में सोचना वास्तव में स्वाभाविक होता है इसने मुझे यह सोचने को मजबूर किया कि मुझे शायद इस बारे में शिक्षा देने के लिए इतना ज्यादा समय नहीं खर्च करना चाहिए, बल्कि इस तरह के प्रश्नों का प्रयोग करना चाहिए, ताकि उनमें ये अवधारणाएं स्वाभाविक तौर पर विकसित हों।
उन्हें उन अभिव्यक्तियों को लेकर बहुत संदेह था जिनके साथ उन्हें शुरू करना था। मुझे ऐसा इसलिए लगा, क्योंकि इसमें एक भिन्न शामिल था –शायद मुझे पूछना चाहिए था। मैंने थोड़ी देर तक इंतजार किया, ताकि वे इस बात से वास्तव में अवगत हो जाएं कि जो संकेत मैं उन्हें देने जा रही हूं, उसपर वे टिके हैं और उसका सम्मान करेंगेः अनुमान लगाना शुरू करने के लिए का अनुमान लगाना। शिवम ने फैसला किया कि लगभग 0.8 होगा, जो तकरीबन 1 है, और इस प्रकार वह अभिव्यक्ति x + 5 होगी। मैंने उनसे पूछा कि क्या वह अधिकतम अथवा न्यूनतम मान होगा, और वे सभी सहमत थे कि वह अधिकतम होगा। ऐसी अभिव्यक्ति के लिए जिसमें शामिल हो मुझे कोई भी संकेत देने की ज़रूरत नहीं पड़ी। सभी सीधे अनुमान करने लगे, क्या होगा – ऐसा लगता है कि मेरे संकेत ने काम किया। उन्होंने कहा कि मान लगभग 4 होगा और इसका मतलब है कि न्यूनतम मान 9 होगा।
तीसरी अभिव्यक्ति को लेकर उनके चेहरों पर परेशानी झलकने लगी। मैंने उनसे पूछा कि उन्हें क्या परेशानी है, तो उन्होंने कहा कि परेशानी घन और वर्ग निकालने में थी। इसलिए, मैंने उन्हें एक सहायक प्रश्न देकर उनकी मदद कीः मैंने उनसे कहा कि वे 3 और 0.1 का घन निकालें, और परिणाम देखें। तरुना ने कहा कि 3 का घन संख्या 3 से बड़ा होगा, लेकिन 0.1 का घन 1 से छोटा होगा। तब मैंने उनसे बस इतना कहा ’अब इस अभिव्यक्ति को देखो’ और उन्होंने तुरन्त ही उत्तर निकाल लिए। एक बार फिर, बगैर उत्साह बढ़ाए, उन्होंने अपने अनुमानों में एक शृंखला की पहचान कर ली।
चारपाई के बारे में कक्षा में वास्तविक उत्सुकता थी। उन्होंने मुझसे पूछा कि चारपाई की लम्बाई और चौड़ाई क्या है। मैंने उन्हें बताया कि उनका अनुमान वहीं से शुरू होता है – यह उनके ऊपर निर्भर है। सभी ने फैसला किया कि उन्हें इसे दो मीटर गुणा एक मीटर मानना चाहिए। लेकिन वहां इस बात पर ज्यादा चर्चा हुई कि वे दोगुना कैसे करेंगे, क्योंकि रस्सी फ्रेम के चारों ओर लपेटी जानी थी। इस बिन्दु पर मैंने उनसे इसपर जोड़े बनाकर काम करने को कहा, और यह भी कि वे बाद में अपनी सोच को पूरी कक्षा के साथ साझा करने के लिए तैयार रहें।
प्रश्न 4 के कारण अत्यधिक चर्चा हुई। इसका वर्णन करने में उन्हें परेशानी हुई–– शुरुआत में ऐसा लगा कि उनके पास भाषा नहीं है। मैंने सोचा कि यदि वे सभी अपनी बातचीत तेज आवाज में करें और अपने विचारों को बताएं तो उन्हें मदद मिलेगी, इसलिए मैंने उनसे कहा कि वे अपनी सोच एक दूसरे को जोड़े में बताएं और जब वे अपनी व्याख्याओं से खुश हों, तो इसे अपनी अभ्यास पुस्तिकाओं में लिखें। इसके बाद हमने कुछ व्याख्याओं को पूरी कक्षा के साथ साझा किया। मैंने ध्यान दिया कि कुछ विद्यार्थियों ने उन बातों में बदलाव किया, जो उन्होंने पूरी कक्षा के साथ चर्चा में निकले परिणाम के रूप में लिखा था। व्याख्याएं शायद बहुत परिष्कृत नहीं थीं, लेकिन मैं उनकी सोच के बारे में विचार करना शुरू करने के उनके प्रयास और उनकी प्रतिबद्धता से बहुत प्रभावित थी – यह करना कोई आसान काम नहीं है! मैंने उन्हें यह बात बताई और यह भी कहा कि मुझे यह करना अभी भी बहुत कठिन लगता है।
अपने शिक्षण अभ्यास के विषय में विचार करना
जब आप अपनी कक्षा के साथ ऐसी कोई गतिविधि करें, तो बाद में सोचे कि क्या ठीक रहा और कहाँ गड़बड़ हुई। ऐसे प्रश्नों की ओर ध्यान दें, जो विद्यार्थियों में रुचि पैदा करे और जिन्हें आपको स्पष्ट करने की आवश्यकता हो। ऐसी बातें ऐसी ’स्क्रिप्ट’ पता करने में सहायक होती हैं, जिससे आप विद्यार्थियों में गणित के प्रति रुचि जगा सकें और उसे मनोरंजक बना सकें। यदि वे कुछ भी समझ नहीं पाते हैं तथा कुछ भी नहीं कर पाते हैं, तो वे शामिल होने में कम रुचि लेंगे।
विचार के लिए रुकें ऐसे चिंतन को गति देने वाले अच्छे सवाल हैं:
|
2 सटीक गणनाओं के साथ अनुमान लगाने की तुलना करना
गतिविधि 1 में आपने विद्यार्थियों से अनुमान लगाने का अभ्यास करने और गणनाओं में शामिल गणितीय सोच प्रक्रियाओं के बारे में सोचना शुरू करने को कहा। अगली गतिविधि इसे आगे बढ़ाती है और आप तथा आपके विद्यार्थियों के लिए सटीक उत्तरों के साथ अनुमानों की तुलना के द्वारा गणितीय प्रक्रियाओं पर ध्यान केन्द्रित करने और विद्यार्थियों के लिए अनुमान लगाने के उद्देश्य से ज्यादा अवगत होने के लिए अधिक अवसर मुहैया कराती है। यह उन प्रश्नों का इस्तेमाल करती है, जिसमें विद्यार्थी सामान्य तौर पर पहले उत्तर का अनुमान लगाने पर विचार नहीं करेंगे बल्कि सीधे सटीक उत्तर निकालने पर काम करने लगते हैं। यह गतिविधि उन्हें रुकने और पहले सोचने को कहती है।
गतिविधि 2: अनुमान लगाना एक मार्गदर्शक के रूप में
अपने विद्यार्थियों से निम्नलिखित पूछें:
इनमें से प्रत्येक प्रश्नों में, पहले उत्तर का अनुमान करें (इसे निकाले बगैर) और तब सटीक उत्तर निकालें। अनुमान (E) और सटीक उत्तर (A) के बीच अन्तर का पता लगाएं।
- मोहन 500 रुपये में कितने किलो चीनी खरीद सकता है यदि चीनी की कीमत 75 रुपये प्रति किलो हो?
- कुछ देशों में तापमान फारेनहाइट (°F) में मापा जाता है; भारत में, तापमान सेल्सियस (°C) में मापा जाता है। तापमानों के दो माप समीकरण
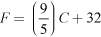 द्वारा संबंधित होते हैं। यदि न्यू ओरलियांस, यूएसए में तापमान 95 °F है, समतुल्य तापमान सेल्सियस में क्या है?
द्वारा संबंधित होते हैं। यदि न्यू ओरलियांस, यूएसए में तापमान 95 °F है, समतुल्य तापमान सेल्सियस में क्या है? - a, b और c किनारों वाले एक त्रिकोण का क्षेत्रफल
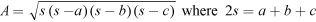 .
. द्वारा दिया गया है, जहां 2s = a + b + c है। एक समबाहु त्रिकोण का क्षेत्रफल निकालें, जिसके किनारे की लम्बाई 4 सेमी है।
जब विद्यार्थियों को एक अनुमान और एक सटीक उत्तर दिया गया हो, तो उनसे पूछें:
क्या आपको लगता है कि आपका अनुमान अच्छा था? इसे सुधारने के लिए आप क्या कर सकते थे? क्या पहले उत्तर का अनुमान लगाने से आपको सटीक उत्तर प्राप्त करने में किसी स्तर पर मदद मिलती है?
क्या उत्तर का अनुमान लगाना आपके विद्यार्थियों के लिए लाभदायक है? क्या वे अनुमान लगाने के प्रति आश्वस्त हैं? यदि नहीं, तो आप और अन्य विद्यार्थी उनकी मदद कैसे करते हैं?
केस स्टडी 2: गतिविधि 2 के उपयोग का अनुभव श्रीमती खान बताती हैं
मैंने विद्यार्थियों से कहा कि वे इसपर व्यक्तिगत रूप से काम करें और बाद में पूरी कक्षा के समक्ष व्याख्या करने के लिए तैयार रहें कि उन्होंने अपना अनुमान कैसे किया। इसके बाद हमने उत्तरों की तुलना की–– कुछ को ही प्रलोभन देना पड़ा और वास्तविक मान का पता चल गया। उन मामलों में मैंने उनसे यह बताने को कहा कि अनुमान की उनकी पद्धतियां क्या थीं। वास्तव में यह मजेदार था, क्योंकि जब वे अनुमान लगाने की प्रक्रिया का वर्णन ठीक उसी तरह करने का प्रयास करने लगे, जैसा सटीक उत्तर प्राप्त करते समय करते थे, तो ठीकठाक अनुमान लगा चुके अन्य विद्यार्थी टिप्पणी और आलोचना करने लगे (निसंदेह, मित्रतापूर्ण और रचनात्मक तरीके से)।
प्रश्न 1 के लिए, राहुल ने कहा कि एक किलो की कींमत 75 रुपये है, इसलिए 2 किलो की कींमत 150– रुपये 300 का मतलब 4 किलो होगा और रुपये 450 का मतलब 6 किलो होगा और चूंकि वंहां ज़रूरत से ज्यादा रुपये थे, इसलिए मात्रा 6 किलो से ज्यादा और 7 किलो से कम होगी।
दूसरा प्रश्न ऐसा नहीं था, जिसके बारे में उन्होंने कभी भी बात करने की कोशिश की हो, इसलिए उन्होंने सबसे पहले इसे हल करने की कोशिश नहीं की –– –– किसी ने भी जिम्मेदारी नहीं ली! इसलिए मैंने स्वीकार किया यह उनके लिए असुविधाजनक हो सकता है और पूछा कि कौन व्याख्या करने का प्रयास करेगा। साक्षी और उषा, जो एक–दूसरे के अगल–बगल बैठी थीं, दोनों ने एक–दूसरे को कोहनी मारने के बाद अपने हाथ उठाए। मैंने ताली बजाकर उनकी ’बहादुरी’ की सराहना की और व्याख्या के साथ एक–दूसरे की सहायता करने के लिए दोनों को आमंत्रित किया। उन्होंने कहा कि वे 95 को 90 मानेंगी और 60 प्राप्त करने के लिए उसमें से 30 घटा देंगी। उन्होंने कहा कि लगभग 2 है, इसलिए दो से भाग देने पर वे अनुमान लगा सकती हैं कि सेल्सियस 30 से अधिक होगा। कोई भी अनुमान करने का बेहतर तरीका नहीं बता सका। फिर हमने चर्चा की कि समस्या को समझने में पहला अनुमान करने का क्या प्रभाव पड़ा। विद्यार्थियों ने महसूस किया कि अनुमान करने की प्रक्रिया का वर्णन सुनकर वे अचानक वह संबंध देख सके कि कैसे सेल्सियस डिग्री फारेनहाइट डिग्री से सम्बन्धित हो सकता है।
प्रश्न 3 इस मामले में दिलचस्प था कि मेरे सहित कोई भी व्यक्ति अनुमान करने का कोई ऐसा तरीका नहीं ढूंढ सका, जो सटीक उत्तर निकालने से भिन्न हो। फिर हमने इस बारे में अच्छी चर्चा की कि ऐसा क्यों था, और इस निष्कर्ष पर पहुंचे कि हमारे सामने कोई तस्वीर, अथवा स्पष्ट समझदारी नहीं थी कि क्षेत्रफल निकालने के लिए दिए गए फार्मूले का कलन विधि से अलग मतलब क्या है।
3 वास्तविक जीवन में अनुमान लगाना
अनुमान का प्रयोग वास्तविक जीवन में हर समय किया जाता है। एनसीएफ (2005) भी सुझाव देता है कि समझदारी बढ़ाने और विषय की प्रासंगिकता बढ़ाने के लिए गणित का प्रयोग अन्य पाठ्यक्रम क्षेत्रों में किया जाता है, और अनुमान कई अन्य क्षेत्रों में उपयोगी विचार है।
अगली गतिविधि में आपके विद्यार्थियों द्वारा भूगोल, इतिहास और स्थानीय रीति–रिवाजों के साथ गणित को जोड़ते हुए वास्तविक जीवन की मात्राओं जैसे कि दूरी, क्षेत्रफल और आयतनों का अनुमान लगाना शामिल है। अनुमान लगाने के लिए ऐसी वस्तुओं और परिदृश्य का प्रयोग किया जा सकता है, जो आपके स्थानीय वातावरण के अनुकूल हों। आप विद्यार्थियों से कह सकते हैं कि वे अपने होमवर्क के हिस्से के रूप में उदाहरण प्रस्तुत करें। यदि आप अथवा आपके विद्यार्थियों की पहुंच इंटरनेट तक है, तो आप बहुत आसानी से ढेर सारी स्थानीय जानकारी प्राप्त कर सकते हैं।
गतिविधि 3: वास्तविक जीवन में अनुमान लगाना
यदि आप अपनी कक्षा के साथ सभी तीन गतिविधियां कर रहे हैं, आप अपने विद्यार्थियों को समूहों में बांटना और विभिन्न समूहों से विभिन्न समस्याओं पर काम कराना चाहेंगे। यह फैसला करें कि आपके समूह में ऐसे सभी विद्यार्थी हों, जो आत्मविश्वासपूर्वक गणित सीखने वाले हों या आप मिश्रित समूह बनाएंगे।
अपने विद्यार्थियों को अपने–अपने समूह में शामिल होने को कहें और उन्हें बताएं कि कौन सी समस्या हल करनी है। कक्षा की दीवारों पर चिपकाने के लिए आप कागज के बड़े टुकड़ों पर समस्याएं लिख सकते हैं।
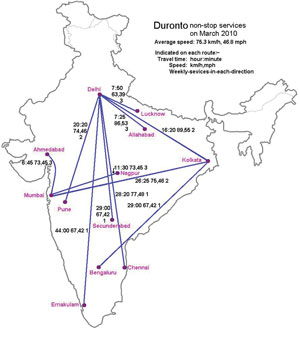
- दूरियों का अनुमान लगाना: चित्र 3 में हमें भारत में दुरन्तो रेल सेवा के बारे में विस्तार से बताया गया है। दो शहरों के बीच प्रत्येक यात्रा के लिए आपको यात्रा समय के साथ ट्रेन की औसत गति किलोमीटर प्रति घंटे के रूप में उपलब्ध कराई जाती है। क्या आप उस समूची दूरी का अनुमान लगा सकते हैं, जो एक व्यक्ति दुरन्तो नेटवर्क का इस्तेमाल करते हुए इस नेटवर्क में सभी शहरों की यात्रा के दौरान तय करेगा?
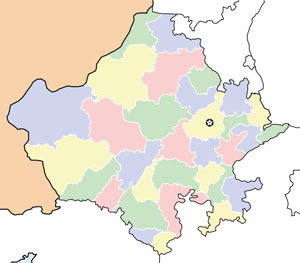
- अनुमानित क्षेत्रफल: अपने राज्य में प्रत्येक जिले के क्षेत्रफल का अनुमान लगाने के तरीके का पता लगाइए (चित्र 4)।
- अनुमानित मात्रा: कोई तीन वस्तुएं चुनिए, जो द्रव की अलग–अलग मात्राएं धारण कर सकती हैं। (कुछ उदाहरण चित्र 5 में दिखाये गये हैं।) वे पानी की कितनी मात्रा धारण कर सकती हैं, इसका अनुमान आप कैसे लगा सकते हैं?
चित्र 5 ऐसी वस्तुओं के चार उदाहरण, जिनमें तरल पदार्थों को रोका जा सकता है
अधिक जानने के लिए संसाधन 2 और 3, स्थानीय संसाधनों का उपयोग करना’’ (Using local resources) और ’’समूहकार्य का उपयोग करना’’ (Using groupwork) पढ़ें।
केस स्टडी 3: गतिविधि 3 के उपयोग का अनुभव श्रीमती अग्रवाल बताती हैं
विद्यार्थियों की ओर से आया पहला प्रश्न था कि ’क्या हमें उन सभी शहरों में जाना होगा जो दुरंतो नेटवर्क से जुड़े हैं?’ तो मैंने कहा हां, उन सभी में जाने की कोशिश करो फिर भी कम से कम दूरी तय करो, और इस बात पर नज़र रखना वाकई उपयोगी होगा कि तुम कहां–कहां गये हो और कहां नहीं गये। उन्हें यह कार्य वाकई पसंद आया – उन्हें इसे पूरा करने के लिए अपना तरीका खुद निकालना था। मैंने यह सुझाव दिया कि वे चार–चार के समूह बना लें, क्योंकि हो सकता है कि इससे बेहतर समाधान ढूँढे जा सकें। इस बारे में काफी चर्चा हुई कि वह केंद्र कौन सा हो, जहां से सभी जगहों पर आना–जाना हो।
साझेदारी के दौरान इस बारे में हमारे बीच काफी दिलचस्प बहस हुई कि यात्रा करने का सबसे अच्छा तरीका क्या था और इस मामले में अनुमान लगाने का उद्देश्य क्या है। वे सभी इस बात से सहमत थे कि इस समस्या पर काम करने के लिए अनुमान ही एकमात्र समझदारी भरा तरीका है, क्योंकि सटीक उत्तर का वास्तव में कोई मतलब नहीं होगा।
प्रश्न 2 में क्षेत्रफल के अनुमान को लेकर वे शुरू में थोड़ा क्रम में थे। उन्होंने कहा कि इस पर काम करने के लिए उन्हें कुछ और जानकारी की आवश्यकता है। हमने चर्चा की कि ऐसा क्यों है और उन्हें क्या आवश्यकता होगी। वे सहमत हुए कि उन्हें एक छोटी सी जानकारी ढूंढन दी जाएगी, जिसे वे एटलस या इंटरनेट से प्राप्त कर सकते हैं। एक ग्रुप ने सबसे छोटे जिले का क्षेत्रफल पता किया, क्योंकि उन्होंने कहा कि इससे उन्हें अन्य जिलों का अनुमान लगाने में मदद मिलेगी। एक अन्य ग्रुप ने निर्णय किया वे अपने जिले का क्षेत्रफल पता लगाएंगे और कि दूसरों के क्षेत्रफल का अनुमान लगाएंगे। तीसरे ग्रुप ने दिए गए मानचित्र का पैमाने पता लगाने की कोशिश की और फिर एक ज्यामितीय सूत्र का उपयोग करके उत्तर प्राप्त करने का निर्णय किया। कई प्रकार के उत्तर आये। फिर हमने उनके अनुमानों को जोड़कर देखा कि उनमें से कौन उनके राज्य के वास्तविक क्षेत्रफल के सबसे नजदीक है। हमने इस समस्या में अनुमान लगाने के उद्देश्य के बारे में और फिर ऐसा करने से उन्होंने जो गणित सीखा उसके बारे में चर्चा की। वे सभी इस बात पर सहमत हुए कि अनुमान लगाना ही एकमात्र समझदारी भरा दृष्टिकोण था, और अलग–अलग आकार वाले राज्यों के क्षेत्रफल का बार–बार अनुमान लगाने से वे यह सोच रहे हैं कि क्षेत्रफल की गणना करने के लिए किस चीज़ पर ध्यान दिया जाना चाहिए।
फिर मात्रा का सवाल आया। उन सभी ने एक वस्तु के रूप में गिलास को चुना। उन्होंने इसका कारण यह बताया कि वे जानते थे कि पेप्सी की एक छोटी बोतल से ऐसे पांच गिलास भर जाते हैं (हालांकि कुछ ने छह गिलास बताया)। तो इसके बाद वे तय कर सकते थे कि अन्य आकारों को भरने के लिए कितने गिलासा भरने होंगे । निःसंदेह, उत्तर विभिन्न प्रकार के थे, क्योंकि उन सभी ने वस्तुओं के आकार का अलग–अलग अनुमान लगाया था। लेकिन उन्होंने अपने उत्तरों के पक्ष में अच्छे तर्क दिये, जो एक शिक्षक के रूप में मेरे लिए संतोषजनक था–
विचार के लिए रुकें
|
4 सारांश
यह यूनिट अनुमान लगाने पर तथा इस बात पर ध्यान देती है कि विद्यार्थी ब्यौरों के बजाय गणितीय विचारों पर ध्यान केंद्रित करने के लिए इस दृष्टिकोण का उपयोग कैसे कर सकते हैं और एक सटीक आंकिक का हिसाब लगाना पाना कितना कठिन होता है। अनुमान लगाने से विद्यार्थियों को यह समझने में मदद मिल सकती है कि वे क्या और क्यों कर रहे हैं और वे परीक्षा में अधिक अंक भी प्राप्त कर सकते हैं, क्योंकि अगर गणना में उनसे कोई चूक हुई हो, तो उन्हें पता चल जाता है।
गतिविधियों में अनुमान लगाने के लिए अनेक विचार शामिल होते हैं जिससे यह ’गणित का हिसाब लगाने’ के समय की जाने वाली एक और मामूली क्रिया नहीं लगती। इससे यह भी पता चलता है कि साथ मिलकर काम करना न केवल विद्यार्थियों को सोचने में मदद देता है, बल्कि उनकी सोच को स्पष्ट अभिव्यक्ति देने का एक कारण भी होता है, जिससे यह वास्तविक बन जाती है और इसे बाद में याद करना आसान हो जाता है।
संसाधन
संसाधन 1: NCF/NCFTE शिक्षण आवश्यकताएं
यह यूनिट NCF (2005) तथा NCFTE (2009) की निम्न शिक्षण आवश्यकताओं से जोड़ता है तथा उन आवश्यकताओं को पूरा करने में आपकी मदद करेगाः
- शिक्षार्थियों को उनके शिक्षण में सक्रिय प्रतिभागी के रूप में देखें न कि सिर्फ ज्ञान प्राप्त करने वाले के रूप में; जिससे ज्ञान निर्माण के लिए उनकी क्षमताओं को प्रोत्साहित किया जा सके; ’रटने की’ पद्धतियों से शिक्षण को दूर ले जाना सुनिश्चित किया जा सके।
- शिक्षण को निजी अनुभव से अर्थ की खोज के रूप में और ज्ञान अर्जन को चिंतनशील शिक्षण की निरंतर विकसित होती प्रक्रिया के रूप में देखें।
- विद्यार्थियों को गणित से डरने के बजाय उसका आनंद उठाना सिखाने के लिए समर्थन।
- गणित को किसी ऐसी चीज़ के रूप में देखने में विद्यार्थियों की मदद करें, जिसके बारे में वे बात करें, जिसके द्वारा संवाद करें, जिसकी आपस में चर्चा करें, और जिसपर साथ मिलकर कार्य करें।
- स्कूली ज्ञान को सामुदायिक ज्ञान से और स्कूल के बाहर के जीवन से जोड़ें।
संसाधन 2: स्थानीय संसाधनों का उपयोग करते हुए
अध्यापन के लिए केवल पाठ्यपुस्तकों का ही नहीं – बल्कि अनेक शिक्षण संसाधनों का उपयोग किया जा सकता है। यदि आप विभिन्न ज्ञानेंद्रियों (दृष्टि, श्रवण, स्पर्श, गंध, स्वाद) का उपयोग करने वाले तरीकों की पेशकश करते हैं, तो आप विद्यार्थियों के सीखने के विभिन्न तरीकों को आकर्षित करेंगे। आपके इर्दगिर्द ऐसे संसाधन उपलब्ध हैं जिनका उपयोग आप कक्षा में कर सकते हैं, और जिनसे आपके विद्यार्थियों की शिक्षण–प्रक्रिया को समर्थन मिल सकता है। कोई भी स्कूल शून्य या जरा सी लागत से अपने स्वयं के शिक्षण संसाधनों को उत्पन्न कर सकता है। इन सामग्रियों को स्थानीय ढंग से प्राप्त करके, पाठ्यक्रम और आपके विद्यार्थियों के जीवन के बीच संबंध बनाए जाते हैं।
आपको अपने नजदीकी पर्यावरण में ऐसे लोग मिलेंगे जो विविध प्रकार के विषयों में पारंगत हैं; आपको कई प्रकार के प्राकृतिक संसाधन भी मिलेंगे। इससे आपको स्थानीय समुदाय के साथ संबंध जोड़ने, उसके महत्व को प्रदर्शित करने, विद्यार्थियों को उनके पर्यावरण की प्रचुरता और विविधता को देखने के लिए प्रोत्साहित करने, और संभवतः सबसे महत्वपूर्ण रूप से, विद्यार्थियों के शिक्षण में समग्र दृष्टिकोण – यानी, स्कूल के भीतर और बाहर शिक्षा को अपनाने की ओर काम करने में सहायता मिल सकती है।
अपनी कक्षा का अधिकाधिक लाभ उठाना
लोग अपने घरों को यथासंभव आकर्षक बनाने के लिए कठिन मेहनत करते हैं। उस पर्यावरण के बारे में सोचना भी महत्वपूर्ण है जहाँ आप अपने विद्यार्थियों को शिक्षित करने की अपेक्षा करते हैं। आपकी कक्षा और स्कूल को पढ़ाई की एक आकर्षक जगह बनाने के लिए आप जो कुछ भी कर सकते हैं उसका आपके विद्यार्थियों पर सकारात्मक प्रभाव होगा। अपनी कक्षा को रोचक और आकर्षक बनाने के लिए आप बहुत कुछ कर सकते हैं – उदाहरण के लिए, आपः
- पुरानी पत्रिकाओं और पुस्तिकाओं से पोस्टर बना सकते हैं
- वर्तमान विषय से संबंधित वस्तुएं और शिल्पकृतियाँ ला सकते हैं
- अपने विद्यार्थियों के काम को प्रदर्शित कर सकते हैं
- विद्यार्थियों को उत्सुक बनाए रखने और नई शिक्षण–प्रक्रिया को प्रेरित करने के लिए कक्षा में प्रदर्शित चीजों को बदलें।
अपनी कक्षा में स्थानीय विशेषज्ञों का उपयोग करना
यदि आप गणित में पैसे या परिमाणों पर काम कर रहे हैं, तो आप बाज़ार के व्यापारियों या दर्जियों को कक्षा में आमंत्रित कर सकते हैं और उन्हें यह समझाने को कह सकते हैं कि वे अपने काम में गणित का उपयोग कैसे करते हैं। वैकल्पिक रूप से, यदि आप कला विषय के अंतर्गत आकृति और आकारों जैसे विषय पर काम कर रहे हैं, तो आप मेहंदी डिजाइनरों को स्कूल में बुला सकते हैं ताकि वे भिन्न–भिन्न आकारों, डिजाइनों, परम्पराओं और तकनीकों को समझा सकें। अतिथियों को आमंत्रित करना तब सबसे उपयोगी होता है जब शैक्षणिक लक्ष्यों के साथ संबंध हर एक व्यक्ति को स्पष्ट होता है और सामयिकता की साझा अपेक्षाएं मौजूद होती हैं।
आपके पास स्कूल समुदाय में विशेषज्ञ उपलब्ध हो सकते हैं जैसे (रसोइया या देखभालकर्ता) जिन्हें विद्यार्थियों द्वारा अपने शिक्षण के संबंध में प्रतिबिंबित किया जा सकता है अथवा वे उनके साथ साक्षात्कार कर सकते हैं; उदाहरण के लिए, पकाने में इस्तेमाल की जाने वाली मात्राओं का पता लगाने के लिए, या स्कूल के मैदान या भवनों पर मौसम संबंधी स्थितियों का कैसे प्रभाव पड़ता है।
बाह्य पर्यावरण का उपयोग करना
आपकी कक्षा के बाहर ऐसे अनेक संसाधन उपलब्ध हैं, जिनका प्रयोग आप अपने पाठों में कर सकते हैं। आप पत्तों, मकड़ियों, पौधों, कीटों, पत्थरों या लकड़ी जैसी वस्तुओं को एकत्रित कर सकते हैं (या अपनी कक्षा से एकत्रित करने को कह सकते हैं)। इन संसाधनों को अंदर लाने से कक्षा में रूचिकर प्रदर्शन तैयार किए जा सकते हैं जिनका संदर्भ पाठों में किया जा सकता है। इनसे चर्चा या प्रयोग आदि करने के लिए वस्तुएं प्राप्त हो सकती हैं जैसे वर्गीकरण से संबंधित गतिविधि, या सजीव या निर्जीव वस्तुएं। बस की समय सारणियों या विज्ञापनों जैसे संसाधन भी आसानी से उपलब्ध हो सकते हैं जो आपके स्थानीय समुदाय के लिए प्रासंगिक हो सकते हैं – इन्हें शब्दों को पहचानने, गुणों की तुलना करने या यात्रा के समयों की गणना करने के कार्य निर्धारित करके शिक्षा के संसाधनों में बदला जा सकता है।
कक्षा में बाहर से वस्तुएं लाई जा सकती हैं– लेकिन बाहरी स्थान भी आपकी कक्षा का विस्तार हो सकते हैं। आम तौर पर सभी विद्यार्थियों के लिए चलने–फिरने और अधिक आसानी से देखने के लिए बाहर अधिक जगह होती है। जब आप सीखने के लिए अपनी कक्षा को बाहर ले जाते हैं, तो वे निम्नलिखित गतिविधियो को कर सकते हैं:
- दूरियों का अनुमान करना और उन्हें मापना
- यह दर्शाना कि वृत्त पर हर बिन्दु केन्द्रीय बिन्दु से समान दूरी पर होता है
- दिन के भिन्न समयों पर परछाइयों की लंबाई रिकार्ड करना
- संकेतों और निर्देशों को पढ़ना
- साक्षात्कार और सर्वेक्षण आयोजित करना
- सौर पैनलों की खोज करना
- फसल की वृद्धि और वर्षा की निगरानी करना।
बाहर, उनका शिक्षण वास्तविकताओं तथा उनके स्वयं के अनुभवों पर आधारित होता है, तथा शायद अन्य संदर्भों में अधिक लागू हो सकता है।
यदि आपके बाहर के काम में स्कूल के परिसर को छोड़ना शामिल हो तो, जाने से पहले आपको स्कूल के मुख्याध्यापक की अनुमति लेनी चाहिए, समय सारणी बनानी चाहिए, सुरक्षा की जाँच करनी चाहिए और विद्यार्थियों को नियम स्पष्ट करने चाहिए। इससे पहले कि आप बाहर जाएं, आपको और आपके विद्यार्थियों को यह बात स्पष्ट रूप से पता होनी चाहिए कि किस संबंध में जानकारी प्राप्त की जाएगी।
संसाधनों का अनुकूलन करना
चाहें तो आप मौजूदा संसाधनों को अपने विद्यार्थियों के लिए कहीं अधिक उपयुक्त बनाने हेतु उन्हें अनुकूलित कर सकते हैं। ये परिवर्तन छोटे से हो सकते हैं किंतु बड़ा अंतर ला सकते हैं, विशेष तौर पर यदि आप शिक्षण को कक्षा के सभी विद्यार्थियों के लिए प्रासंगिक बनाने का प्रयास कर रहे हैं। उदाहरण के लिए, आप स्थान और लोगों के नाम बदल सकते हैं यदि वे दूसरे राज्य से संबंधित है, या गाने में व्यक्ति के लिंग को बदल सकते हैं, या कहानी में शारीरिक रूप से अक्षम बच्चे को शामिल कर सकते हैं। इस तरह से आप संसाधनों को अधिक समावेशी और अपनी कक्षा और उनकी शिक्षण–प्रक्रिया के उपयुक्त बना सकते हैं।
साधन संपन्न होने के लिए अपने सहकर्मियों के साथ काम करें; संसाधनों को विकसित करने और उन्हे अनुकूलित करने के लिए आपके बीच ही आपको कई कुशल व्यक्ति मिल जाएंगे। एक सहकर्मी के पास संगीत, जबकि दूसरे के पास कठपुतलियाँ बनाने या कक्षा के बाहर के विज्ञान को नियोजित करने के कौशल हो सकते हैं। आप अपनी कक्षा में जिन संसाधनों को उपयोग करते हैं उन्हें अपने सहकर्मियों के साथ साझा कर सकते हैं ताकि अपने स्कूल के सभी क्षेत्रों में एक प्रचुर शिक्षण पर्यावरण बनाने में आप सबकी सहायता हो सके।
संसाधन 3: समूहकार्य का उपयोग करना
समूहकार्य एक व्यवस्थित, सक्रिय, अध्यापन कार्यनीति है जो विद्यार्थियों के छोटे समूहों को एक आम लक्ष्य की प्राप्त के लिए मिलकर काम करने के लिए प्रोत्साहित करती है। ये छोटे समूह संरचित गतिविधियों के माध्यम से अधिक सक्रिय और अधिक प्रभावी ढंग से सीखने की प्रक्रिया को बढ़ावा देते हैं।
समूह में कार्य करने के लाभ
समूह में कार्य करना आपके विद्यार्थियों को सोचने, संवाद कायम करने, समझने और विचारों का आदान–प्रदान करने और निर्णय लेने के लिए प्रोत्साहित करके सीखने के लिए प्रेरित करने का बहुत ही प्रभावी तरीका हो सकता है। आपके विद्यार्थी दूसरों को सिखा भी सकते हैं और उनसे सीख भी सकते हैं: यह सीखने का एक सशक्त और सक्रिय तरीका है।
समूहकार्य में विद्यार्थियों का समूहों में बैठना ही काफी नहीं होता है; इसमें स्पष्ट उद्देश्य के साथ सीखने के साझा कार्य पर काम करना और उसमें योगदान करना शामिल होता है। आपको इस बात को लेकर स्पष्ट होना होगा कि आप सीखने के लिए समूहकार्य का उपयोग क्यों कर रहे हैं और जानना होगा कि यह भाषण देने, जोड़ी में कार्य या विद्यार्थियों के स्वयं अपने बलबूते पर कार्य करने के ऊपर वरीयता देने योग्य क्यों है। इस तरह समूहकार्य को सुनियोजित और प्रयोजनपूर्ण होना चाहिए।
समूहकार्य को नियोजित करना
आप समूहकार्य का उपयोग कब और कैसे करेंगे यह इस बात पर निर्भर करेगा कि अध्याय के अंत तक आप कौन सी सीखने की प्रक्रिया पूरी करना चाहते हैं। समूहकार्य को आप अध्ययन के आरंभ, अंत या उसके बीच में शामिल कर सकते हैं, लेकिन आपको पर्याप्त समय का प्रावधान करना होगा। आपको उस काम के बारे में जो आप अपने विद्यार्थियों से पूरा करवाना चाहते हैं और समूहों को संगठित करने के सर्वोत्तम तरीके के बारे में सोचना होगा।
एक शिक्षक के रूप में, आप सुनिश्चित कर सकते हैं कि समूहकार्य सफल हो यदि आप निम्न के बारे में पहले से योजना बनाते हैं:
- सामूहिक गतिविधि के लक्ष्य और अपेक्षित परिणाम
- गतिविधि के लिए आवंटित समय, जिसमें कोई भी प्रतिक्रिया या सारांश कार्य शामिल है
- समूहों को कैसे बाँटें (कितने समूह, प्रत्येक समूह में कितने विद्यार्थी, समूहों के लिए मापदंड)
- समूहों को कैसे संगठित करें (समूह के विभिन्न सदस्यों की भूमिका, आवश्यक समय, सामग्रियाँ, रिकार्ड करना और रिपोर्ट करना)
- कोई भी आकलन कैसे किया और रिकार्ड किया जाएगा (व्यक्तिगत आकलनों को सामूहिक आकलनों से अलग पहचानने का ध्यान रखें)
- समूहों की गतिविधियों पर आप कैसे निगरानी रखेंगे।
समूहकार्य के काम
वह काम जो आप अपने विद्यार्थियों को पूरा करने को कहते हैं वह इस पर निर्भर होता है कि आप उन्हें क्या सिखाना चाहते हैं। समूहकार्य में भाग लेकर, वे एक–दूसरे को सुनने, अपने विचारों को समझाने और आपसी सहयोग से काम करने जैसे कौशल सीखेंगे। तथापि, उनके लिए मुख्य लक्ष्य है जो विषय आप पढ़ा रहे हैं उसके बारे में कुछ सीखना। कार्यों के कुछ उदाहरणों में निम्नलिखित शामिल हो सकते हैं:
- प्रस्तुतिकरण: विद्यार्थी समूहों में काम करके शेष कक्षा के लिए प्रस्तुतिकरण तैयार कर सकते हैं। यह तब सबसे बढ़िया काम करता है जब प्रत्येक समूह के पास विषय का अलग अलग पहलू होता है, ताकि उन्हें एक ही विषय को कई बार सुनने की बजाय एक दूसरे की बात सुनने के लिए प्रेरित किया जा सके। प्रस्तुतिकरण करने के लिए प्रत्येक समूह को दिए गए समय के बारे में काफी सख्ती बरतें और अच्छे प्रस्तुतिकरण के लिए मापदंडों का एक समुच्चय तय करें। इन्हें अध्याय से पहले बोर्ड पर लिखें। विद्यार्थी मापदंडों का उपयोग अपने प्रस्तुतिकरण की योजना बनाने और एक दूसरे के काम का आकलन करने के लिए कर सकते हैं। मापदंडों में निम्नलिखित शामिल हो सकते हैं:
- क्या प्रस्तुतिकरण स्पष्ट था?
- क्या प्रस्तुतिकरण सुसंरचित था?
- क्या प्रस्तुतिकरण से मैंने कुछ सीखा?
- क्या प्रस्तुतिकरण ने मुझे सोचने पर मजबूर किया?
समस्या का हल करना: विद्यार्थी किसी समस्या या समस्याओं की श्रृंखला को हल करने के लिए समूहों में काम करते हैं। इसमें विज्ञान में प्रयोग करना, गणित में समस्याओं को हल करना, अंग्रेजी में किसी कहानी या कविता का विश्लेषण करना, या इतिहास में प्रमाण का विश्लेषण करना शामिल हो सकता है।
किसी शिल्पकृति या उत्पाद का सृजन करना: विद्यार्थी किसी कहानी, नाटक के अंश, संगीत के अंश, किसी अवधारणा को समझाने के लिए मॉडल, किसी मुद्दे पर समाचार रिपोर्ट या जानकारी का सारांश बनाने या किसी अवधारणा को समझाने के लिए पोस्टर को विकसित करने के लिए समूहों में काम करते हैं। नए विषय के आरंभ में विचारमंथन या दिमागी नक्शा बनाने के लिए समूहों को पाँच मिनट देकर आप इस बारे में बहुत कुछ जान सकेंगे कि उन्हें पहले से क्या पता है, और इससे अध्याय को उपयुक्त स्तर पर स्थापित करने में आपको मदद मिलेगी।
- विभेदित काम: समूहकार्य अलग अलग उम्रों या दक्षता स्तरों वाले विद्यार्थियों को किसी उपयुक्त काम पर मिलकर काम करने का अवसर प्रदान करता है। उच्च उपलब्धि वालों को काम को स्पष्ट करने के अवसर से लाभ मिल सकता है, जबकि कम उपलब्धि वाले विद्यार्थियों को कक्षा की बजाय समूह में प्रश्न पूछना अधिक आसान लग सकता है, और वे अपने सहपाठियों से सीखेंगे।
- चर्चा: विद्यार्थी किसी मुद्दे पर विचार करते हैं और एक निष्कर्ष पर पहुँचते हैं। इसके लिए आपकी ओर से काफी तैयारी की जरूरत पड़ सकती है ताकि सुनिश्चित हो कि विद्यार्थियों के पास विभिन्न विकल्पों पर विचार करने के लिए पर्याप्त ज्ञान है, लेकिन किसी चर्चा या वाद–विवाद को आयोजित करना आप और उन, दोनों के लिए बहुत लाभदायक हो सकता है।
समूहों को संगठित करना
चार या आठ के समूह आदर्श होते हैं लेकिन यह आपकी कक्षा के आकार, भौतिक पर्यावरण और फर्नीचर, तथा आपकी कक्षा की दक्षता और उम्र के दायरे पर निर्भर करेगा। आदर्श रूप से समूह में हर एक को एक दूसरे से मिलने, बिना चिल्लाए बातचीत करने और समूह के परिणाम में योगदान करना चाहिए।
- तय करें कि आप विद्यार्थियों को कैसे और क्यों समूहों में विभाजित करेंगे; उदाहरण के लिए, आप समूहों को मित्रता, रुचि या मिश्रित दक्षता के अनुसार विभाजित कर सकते हैं। अलग अलग तरीकों से प्रयोग करें और समीक्षा करें कि प्रत्येक कक्षा के लिए सर्वोत्तम ढंग क्या है।
- इस बात की योजना बनाएं कि समूह के सदस्यों को आप क्या भूमिकाएं देंगे (उदाहरण के लिए, नोट्स लेने वाला, प्रवक्ता, टाइम कीपर या उपकरण का संग्रहकर्ता), और कि इसे कैसे स्पष्ट करेंगे।
समूहकार्य का प्रबंधन करना
अच्छे समूहकार्य को प्रबंधित करने के लिए आप दिनचर्याएं और नियम निर्धारित कर सकते हैं। जब आप समूहकार्य का नियमित रूप से उपयोग करते हैं, तब विद्यार्थियों को पता चल जाता है कि आप क्या चाहते हैं और वे उसे आनंदमय पाएंगे। आरंभ में टीमों और समूहों में मिलकर काम करने के लाभों को पहचानने के लिए आपकी कक्षा के साथ काम करना एक अच्छा विचार होता है। आपको चर्चा करनी चाहिए कि अच्छा समूहकार्य बर्ताव क्या होता है और संभव हो तो ’नियमों’ की एक सूची बना सकते हैं जिसे प्रदर्शित किया जा सकता है; उदाहरण के लिए, ’एक दूसरे के लिए सम्मान’, ’सुनना’, ’एक दूसरे की सहायता करना’, ’एक विचार से अधिक को आजमाना’ आदि।
समूहकार्य के बारे में स्पष्ट मौखिक अनुदेश देना महत्वपूर्ण है जिसे ब्लैकबोर्ड पर संदर्भ के लिए लिखा भी जा सकता है। आपकोः
अपनी योजना के अनुसार अपने विद्यार्थियों को उन समूहों की ओर निर्देशित करना होगा जिनमें वे काम करेंगे। ऐसा आप शायद कक्षा में ऐसे स्थानों को निर्दिष्ट करके कर सकते हैं जहाँ वे काम करेंगे या किसी फर्नीचर या विद्यालय के बैगों को हटाने के बारे में अनुदेश देकर कर सकते हैं।
- कार्य के बारे में बहुत स्पष्ट होना और उसे बोर्ड पर लघु अनुदेशों या चित्रों के रूप में लिखना चाहिए। अपने शुरू करने से पहले विद्यार्थियों को प्रश्न पूछने की अनुमति प्रदान करें।
अध्याय के दौरान, कमरे में घूमकर देखें और जाँचें कि समूह किस प्रकार काम कर रहे हैं। यदि वे कार्य से विचलित हो रहे हैं या अटक रहे हैं तो जहाँ जरूरत हो वहाँ सलाह प्रदान करें।
आप कार्य के दौरान समूहों को बदलना चाह सकते हैं। जब आप समूहकार्य के बारे में आत्मविश्वास महसूस करने लगें तब दो तकनीकें आजमाई जा सकती हैं – वे बड़ी कक्षा को प्रबंधित करते समय खास तौर पर उपयोगी होती हैं:
- ’विशेषज्ञ समूह’: प्रत्येक समूह को अलग अलग कार्य दें, जैसे विद्युत उत्पन्न करने के एक तरीके पर शोध करना या किसी नाटक के लिए किरदार विकसित करना। एक उपयुक्त समय के बाद, समूहों को पुनर्गठित करें ताकि हर नया समूह सभी मूल समूहों से आए एक ’विशेषज्ञ’ से बने। फिर उन्हें ऐसा काम दें जिसमें सभी विशेषज्ञों के ज्ञान की तुलना करना शामिल हो जैसे निश्चय करना कि किस तरह के पॉवर स्टेशन का निर्माण करना है या नाटक के अंश को तैयार करने का निर्णय करना।
’दूत’: यदि काम में कुछ बनाना या किसी समस्या का हल करना शामिल है, तो कुछ देर बाद, हर समूह से किसी अन्य समूह को एक दूत भेजने के कहें। वे विचारों या समस्या के हलों की तुलना कर सकते हैं और फिर वापस अपने समूह को सूचित कर सकते हैं। इस तरह से, समूह एक दूसरे से सीख सकते हैं।
काम के अंत में, इस बात का सारांश बनाएं कि क्या सीखा गया है और आपको नज़र आने वाली गलतफहमियों को सही करें। आप चाहें तो हर समूह की प्रतिक्रिया सुन सकते हैं, या केवल उन एक या दो समूहों से पूछ सकते हैं जिनके पास आपको लगता है कि अच्छे विचार हैं। विद्यार्थियों की रिपोर्टिंग को संक्षिप्त रखें और उन्हें अन्य समूहों के काम पर प्रतिक्रिया देने को प्रोत्साहित करें, जिसमें उन्हें पहचानना चाहिए कि क्या अच्छी तरह से किया गया है, क्या दिलचस्प था और किसे आगे और विकसित किया जा सकता है।
यदि आप अपनी कक्षा में समूहकार्य को अपनाना चाहते हैं तो भी आपको कभी–कभी इसका नियोजन कठिन लग सकता है क्योंकि कुछ विद्यार्थीः
- सक्रिय सीखने की प्रक्रिया का प्रतिरोध करते हैं और उसमें संलग्न नहीं होते
- हावी होने लगते हैं
- खराब अंतर्वैयत्तिक (inter personal) कौशलों या आत्मविश्वास के अभाव के कारण भाग नहीं लेते हैं।
समूहकार्य में प्रभावी बनने के लिए, शिक्षण के परिणाम कितनी हद तक पूरे हुए और आपके विद्यार्थियों ने कितनी अच्छी तरह से प्रतिक्रिया की (क्या वे सभी लाभान्वित हुए?) जैसी बातों पर विचार करने के अलावा, उपरोक्त सभी बिंदुओं पर विचार करना महत्वपूर्ण होता है। समूह के काम, संसाधनों, समय–सारणियों या समूहों की रचना में किसी भी समायोजन पर विचार करें और सावधानीपूर्वक उनकी योजना बनाएं।
शोध ने सुझाया है कि समूहों में सीखने की प्रक्रिया को हर समय ही विद्यार्थियों की उपलब्धि पर सकारात्मक प्रभावों से युक्त होना जरूरी नहीं है, इसलिए आप हर अध्याय में इसका उपयोग करने के लिए बाध्य नहीं हैं। आप चाहें तो समूहकार्य का उपयोग एक पूरक तकनीक के रूप में कर सकते हैं, उदाहरण के लिए विषय परिवर्तन के बीच अंतराल या कक्षा में चर्चा को अकस्मात शुरु करने के साधन के रूप में कर सकते हैं। इसका उपयोग विवाद को हल करने या कक्षा में अनुभव आधारित शिक्षण गतिविधियाँ और समस्या का हल करने के अभ्यास शुरू करने या विषयों की समीक्षा करने के लिए भी किया जा सकता है।
अतिरिक्त संसाधन
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- Class X maths study material: http://www.zietmysore.org/ stud_mats/ X/ maths.pdf
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- OpenLearn: http://www.open.edu/ openlearn/
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Mathcelebration: http://www.mathcelebration.com/
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Maths is Fun: http://www.mathsisfun.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 5 (‘Exploring Numbers’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Central Board of Secondary Education’s books and support material (also including the Teachers Manual for Formative Assessment – Mathematics (Class IX)) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
अभिस्वीकृतियाँ
तृतीय पक्षों की सामग्रियों और अन्यथा कथित को छोड़कर, यह सामग्री क्रिएटिव कॉमन्स एट्रिब्यूशन–शेयरएलाइक लाइसेंस के अंतर्गत उपलब्ध कराई गई है (http://creativecommons.org/licenses/by-sa/3.0/)। नीचे दी गई सामग्री मालिकाना हक की है तथा इस परियोजना के लिए लाइसेंस के अंतर्गत ही उपयोग की गई है, तथा इसका Creative Commons लाइसेंस से कोई वास्ता नहीं है। इसका अर्थ यह है कि इस सामग्री का उपयोग अननुकूलित रूप से केवल TESS-India परियोजना के भीतर किया जा सकता है और किसी भी बाद के OER संस्करणों में नहीं। इसमें TESS-India, OU और UKAID लोगो का उपयोग भी शामिल है।
इस यूनिट में सामग्री को पुनः प्रस्तुत करने की अनुमति के लिए निम्न स्रोतों का कृतज्ञतापूर्ण आभारः
चित्र 1 (Figure 1): © Thamizhpparithi Maari http://commons.wikimedia.org/wiki/File:A_road_side_fruit_juice_stall.jpg यह फाइल Creative Commons Attribution-Share Alike 3.0 Unported लाइसेंस के अंतर्गत लाइसेंसशुदा है।–
चित्र 2 (Figure 2): © रचनाकार (author): http://upload.wikimedia.org/ wikipedia/ commons/ 2/ 24/ Cot- rope,traditional_-Tamil_Nadu52.JPG
चित्र 3 (Figure 3): © Harvardton, http://commons.wikimedia.org/wiki/File:Indian_Railways_Duronto_map.gif –यह फाइल Creative Commons Attribution-Share Alike 3.0 Unported लाइसेंस के अंतर्गत लाइसेंसशुदा है।
चित्र 4 (Figure 4): http://d-maps.com/ carte.php?num_car=32397&lang=en ©D-maps.com अनपोर्टेड लाइसेंस के अधीन लाइसेंसीकृत है।
चित्र 5 (Figure 5): गिलासः © drinking glass: © Derek Jenson (Tysto), http://upload.wikimedia.org/ wikipedia/ commons –यह फाइल Creative Commons Attribution-Share Alike 3.0 Unported लाइसेंस के अंतर्गत लाइसेंसशुदा है; बाल्टीः © MarlonBSB: http://commons.wikimedia.org/wiki/File:Balde.PNG –यह फाइल Creative Commons Attribution-Share Alike 3.0 Unported लाइसेंस के अंतर्गत लाइसेंसशुदा है; पानी की टंकीः http://www.hrp.co; ghatam: © Sven Petersen, http://commons.wikimedia.org/wiki/File:Ghatam.jpg?uselang=en-gb–यह फाइल Creative Commons Attribution-Share Alike 3.0 Unported लाइसेंस के अंतर्गत लाइसेंसशुदा है।
कॉपीराइट के स्वामियों से संपर्क करने का हर प्रयास किया गया है। यदि किसी को अनजाने में अनदेखा कर दिया गया है, तो पहला अवसर मिलते ही प्रकाशकों को आवश्यक व्यवस्थाएं करने में हर्ष होगा।
वीडियो (वीडियो स्टिल्स सहित): भारत भर के उन अध्यापक शिक्षकों, मुख्याध्यापकों, अध्यापकों और विद्यार्थियों के प्रति आभार प्रकट किया जाता है जिन्होंने उत्पादनों में दि ओपन यूनिवर्सिटी के साथ काम किया है।