Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Tuesday, 10 March 2026, 8:09 AM
गणितीय तर्क शक्ति का विकास करना : गणितीय प्रमाण
यह इकाई किस बारे में है
गणितीय प्रमाण को अक्सर गणित का एक महत्वपूर्ण आधार माना जाता है। व्यावसायिक गणितज्ञ विकासशील अनुमान लगाते हैं फिर उसपर कार्य करते हैं कि क्या वे अनुमान सभी स्थितियों में लागू होते हैं, कुछ स्थितियों में लागू हैं या किसी भी स्थिति में लागू नहीं हैं। इसपर वे बहुत समय बिताते हैं। प्रमाण और औचित्य परिशुद्ध होने चाहिए और ज्ञात गणितीय तथ्यों और गुणो पर आधारित होने चाहिए। प्रमाणित करने की यह प्रक्रिया गणित की समझ और ज्ञान की जाँच के बीच की जाती है, और गणितीय विचारों और अवधारणाओं के बीच संबंध स्थापित किए जाते हैं।
गणित की समझ विकसित करने के लिए कक्षाओं में प्रमाणित करने की प्रक्रिया भी एक अच्छी गतिविधि हो सकती है। इससे विद्यार्थी गतिविधियों में व्यस्त रहते हैं और यह वास्तविक गणितज्ञों के द्वारा की गयी गतिविधि है। परन्तु विद्यालयों में अक्सर विद्यार्थी यह समझते हैं कि गणित में प्रमाणित करने की प्रक्रिया को रटकर याद किया जाता और सीखा जाता है। यह विधि केवल इस बात पर जोर देती है कि गणित तथ्यों और प्रक्रियाओं को कंठस्थ करने के बारे मे है, जबकि प्रमाण की अवधारणा का उद्देश्य अक्सर स्पष्ट नहीं किया जाता।
इस इकाई में आप गणितीय प्रमाण के बारे में तथा इस बारे में सोचेंगे कि किस प्रकार इसका उपयोग अपने विद्यार्थियों की गणितीय समझ को और बेहतर बनाने में किया जा सकता है। आप सीखेंगे कि अपने विद्यार्थियों को मौखिक विवेक बोध में और बेहतर बनने में मदद कैसे करें और वे चर्चाओं से प्रभावी रूप से कैसे सीख सकते हैं।
आप इस इकाई में क्या सीख सकते हैं
विद्यार्थियों को किस प्रकार अपनी सोच प्रक्रियाओं को वर्णित करने और स्पष्ट करने के लिए सक्षम करें।
बातचीत के माध्यम से विद्यार्थियों का शिक्षण किस प्रकार सुगम बनाएँ।
- प्रमाण शिक्षण में उपलब्धि के विभिन्न स्तरों के समाधान के लिए कुछ सुझाव।
इस इकाई का संबंध संसाधन 1 में दी गई एनसीएफ–2005 (NCF 2005) और एनसीएफटीई (2009) शिक्षण आवश्यकताओं से है।
1 विद्यालयों में गणितीय प्रमाण क्यों सिखाए जाएँ?
दुनियाभर में इस प्रकार की कई चर्चाएँ हो रही हैं कि क्या गणितीय प्रमाण विद्यालय की पाठ्यचर्या का भाग होना चाहिए। अध्यापकों को अक्सर प्रमाण पढ़ाने में कठिनाई होती है और विद्यार्थियों को अक्सर सीखने में परेशानी होती है। यह भी हमेशा स्पष्ट नहीं होता कि प्रमाण पर काम करने से किस प्रकार की गणितीय शिक्षा प्राप्त होती है। कुछ देशों में गणितीय प्रमाण की शिक्षा पूरी तरह से बंद ही कर दी गई है, यद्यपि अन्य देश इसे गणित में विवेक बोध के रूप में देखते हैं। भारत में, गणितीय प्रमाण अभी भी विद्यालय की पाठ्यचर्या का भाग है और कक्षा 9 और 10 की पाठ्यपुस्तकों के कई अध्यायों में गणितीय प्रमाण शामिल होते हैं।
विद्यालयों में गणितीय प्रमाण पर काम करने से मिलने वाली गणितीय सोच से जुड़ी कई सकारात्मक बातें हैं। शोधकर्ता बताते हैं कि गणितीय प्रमाण पर काम करने से कई तरह के गणितीय शिक्षण अवसर प्राप्त होते हैं। हन्ना (2000) ने इसका सारांश ऐसे बतायाः
- किसी कथन की सत्यता का सत्यापन
- यह सत्य क्यों है, इस बात का वर्णन करके व्याख्या
- विभिन्न परिणामों को सूक्तियों, मुख्य अवधारणाओं और प्रमेयों की किसी निगमनात्मक प्रणाली में व्यवस्थित करके व्यवस्थापन
- नए परिणामों की खोज या आविष्कार
- गणितीय ज्ञान प्रसारित करने के लिए संचार
- किसी प्रयोगाश्रित सिद्धात का निर्माण
- किसी परिभाषा का मतलब या किसी मान्यता के परिणामों की खोज
- सुविज्ञात तथ्यों का नई रूपरेखा में समावेशन और इस प्रकार इसे किसी एकदम नए नजरिए से देखना।
यह इकाई इस बात की खोजबीन करेगी और सुझाव देगी कि गणितीय प्रमाण की प्रक्रिया का उपयोग किस प्रकार उपर्युक्त जैसे शिक्षण अवसरों पर काम करके विद्यार्थियों में गणित की समझ बढ़ाने के उपकरण के रूप में किया जा सकता है।
विचार के लिए रुकें विद्यालय की पाठ्यचर्या में गणितीय प्रमाण के बारे में आपके विचार और राय क्या हैं? क्या इसे उसमें होना चाहिए? क्या आप इन शोधकर्ताओं द्वारा सुझाए गए शिक्षण अवसरों की सूची से सहमत हैं? किन–किन को आप सबसे महत्वपूर्ण मानते हैं? क्या इस प्रकार का गणितीय शिक्षण अभी आपकी कक्षा में होता है? यदि ऐसा है, तो आप इसे कैसे करते हैं? यदि नहीं, तो क्या आपके पास इस बारे में कोई विचार है कि आप अपने वर्तमान अभ्यास में क्या बदलना चाहेंगे? |
2 क्या यह प्रमाण है?
गणितीय प्रमाण विज्ञान और कानून जैसे अन्य विषयों की प्रमाण से अलग है क्योंकि तर्क–वितर्क में हर चरण ज्ञात और निर्विवादित तथ्यों पर आधारित होना चाहिए – प्रमाण प्रयोगाश्रित साक्ष्य पर आधारित नहीं हो सकता। इसका मतलब यह है कि गणित में आप बस आवृत्तियों का निरीक्षण करके यह नहीं कह सकते है कि ’यह हमेशा सत्य है’। गणित में, प्रमाणों के सभी स्वीकार्य औचित्य या स्थापित कथनों, और तर्क के नियमों पर आधारित होने चाहिए।
सीखने के लिए, और नए शिक्षण का बोध करने के लिए विद्यार्थियों को अपने मौजूदा ज्ञान और अनुभव को जोड़ने में सक्षम होना चाहिए, जो सीधे औपचारिक प्रमाण में जाते समय करना कठिन होता है। इस इकाई के शेष भाग में गणितीय प्रमाण के महत्वपूर्ण पहलुओं को पहचानने और उनका विकास करने में विद्यार्थियों की सहायता करने के तरीके सुझाए गए हैं, जिनमें शामिल हैं:
- यह तर्क कि गणितीय प्रमाण अनुभवसिद्ध साक्ष्य पर आधारित नहीं होते
- गणितीय गुणधर्मों को जानना और पुनः याद करना
- प्रभावी तर्क–वितर्क तकनीकों का विकास
- पहले से ज्ञात बातों पर निर्माण।
कभी–कभी यह जानना कठिन होता है कि गणितीय विवेक बोध को कब ’प्रमाण’ माना जा सकता है या कब नहीं। इसका एक उदाहरण नीचे दिए गए परिदेृश्य में बताया गया है, जिसमें श्रीमती कपूर ने अपने विद्यार्थियों से पूछा कि वे इस बात को कैसे सिद्ध करेंगे कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है।
केस स्टडी 1: श्रीमती कपूर ने अपने विद्यार्थियों से कहा कि वे इस बात सिद्ध करें कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है।
| शिक्षकः | किसी त्रिभुज के अंदर के तीनों कोणों का योग कितना होता है ? |
| विद्यार्थीः | 180°. |
| शिक्षकः | पक्का? |
| विद्यार्थीः | हाँ, बिल्कुल। |
| शिक्षकः | आप कैसे जानते हो कि इतना ही होता है? |
| विद्यार्थीः | क्योंकि...आपने हमें बताया था और पुस्तक में भी यही लिखा है। |
| शिक्षकः | ठीक है, अब मैं चाहती हूँ कि आप एक पल के लिए यह सोचें कि आप इस बात को गणितीय रूप से कैसे सिद्ध करेंगे कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है। यह एक गणितीय साक्ष्य है, इसलिए आपका कारण विस्तृत और उचित होना चाहिए। कल्पना कीजिए कि आप एक गणितज्ञ हैं और भारत के प्रधानमंत्री को यह विश्वास दिलाना चाहते हैं – आप यह कैसे करेंगे? इस बारे में सोचें कि आप त्रिभुजों और गणितीय प्रमाण के बारे में पहले से क्या जानते हैं। अपने विचारों की चर्चा पहले अपने साथी से करें। ऐसा करने के लिए मैं आपको पहले पाँच मिनट दूँगी। |
[पाँच मिनट बाद।] | |
| तो आप प्रधानमंत्री को यह विश्वास दिलाने के लिए क्या कहेंगे कि किसी त्रिभुज के आंतरिक कोणों का योग हमेशा 180° होता है? | |
| विद्यार्थी 1: | हम कहेंगे कि जब आप किसी त्रिभुज के आंतरिक कोणों को मापते हैं और उन्हें जोडत़े हैं, तो आपको हमेशा 180° मिलता है। आप यह कितने भी, और किसी भी प्रकार के त्रिभुजों के साथ कर सकते हैं। |
| विद्यार्थी 2: | हम कहेंगेः कागज के एक टुकड़े पर एक त्रिभुज बनाइए। इसे काटिए। कोने फाड़िए और इन कोनों को पास–पास रखिए। वे हमेशा एक सरल रेखा बनाते हैं। जैसा कि हमें ज्ञात है कि किसी सरल रेखा के कोणों का योग 180° होता है, इसलिए हम यह नतीजा निकाल सकते हैं कि किसी त्रिभुज के आंतरिक कोणों का योग भी 180° होता है। किसी भी त्रिभुज के लिए यह ऐसा ही होगा। |
| शिक्षकः | आप क्या सोचते हैं, कक्षा – क्या आप गणितीय प्रमाणों के इन विचारों से सहमत हैं? क्या प्रधानमंत्री को विश्वास होगा? क्या उन्हें होना चाहिए? |
विचार के लिए रुकें इस बारे में सोचें कि ये विचार किस हद तक वास्तव में गणितीय प्रमाण हैं। क्या कोई अन्य तरीका है जिससे प्रमाण दिया जा सके? इन प्रमाणों को कैसे चुनौती दी जा सकती है? |
3 गणितीय गुणधर्मों और तथ्यों को जानना
श्रीमती कपूर की कक्षा के विद्यार्थी इस बात के कुछ उदाहरण लेकर आए कि वे कोई गणितीय प्रमाण कैसे तैयार कर सकते हैं। हालाँकि, इनमें से किसी को भी गणितीय प्रमाण नहीं माना जा सकता, क्योंकि उपयोग किए गए तर्क पूरी तरह से स्वीकृत या स्थापित कथन नहीं थे। यद्यपि दूसरे सुझाव में इस तथ्य का उपयोग किया गया था कि किसी रेखा के कोणों का योग 180° होता है, लेकिन यह ’प्रमाण’ नहीं है कि तीन कोण हमेशा ’फिट’ होंगे। विद्यार्थी यह तर्क–वितर्क कर सकते हैं कि यह ’काम’ करेगा ही, लेकिन ऐसा औचित्य अनुभवसिद्ध साक्ष्य पर आधारित है, न कि किसी त्रिभुज के कोणों के गणितीय गुणधर्मों पर। प्रमेयों को सिद्ध करने का काम मौजूदा प्रमेयों और अभिगृहीतों के आधार पर किया जा सकता है; हालाँकि उन्हें आधार बनाकर कुछ करने से पहले आपको इनमें से कुछ बातें जाननी होंगी! जब आप कुछ को जान लेंगे, तो आप इनमें से अन्य कई का निगमन कर सकते हैं और अपनी स्वयं की उपप्रमेय बना सकते हैं।
गतिविधि 1 में कुछ ऐसे स्थापित और स्वीकृत कथन दिए गए हैं, जो विद्यालय के गणित में उपयोगी होते हैं। कुछ शास्त्रीय ज्यामिति से लिए गए हैं और उपरोक्त प्रमाण में उपयोगी हैं, लेकिन उदाहरण यह भी स्पष्ट करते हैं कि प्रमेयों का उपयोग ज्यामिति के अलावा कई अन्य क्षेत्रों में भी होता है। सूची में और चीज़ें जोड़ना, तथा दिए गए कथनों से अपने स्वयं के कुछ कथन निकालकर लिखने के लिए अपनी कल्पनाशीलता और प्राकृतिक निगमन कला का उपयोग करना विद्यार्थियों का काम है। ऐसी सोच को उकसाने के लिए यह वाक्य बहुत अच्छा हैः ’जब मुझे कुछ पता चलता है, तो मुझे कुछ और भी पता चलता है।’ ऐसा करके, विद्यार्थी विभिन्न अवधारणाओं के बीच संबंध भी स्थापित करेंगे और निगमन के अपने कौशल का अभ्यास करना शुरू करेंगे।
इस यूनिट में अपने विद्यार्थियों के साथ गतिविधियों के उपयोग का प्रयास करने के पहले अच्छा होगा कि आप सभी गतिविधियों को पूरी तरह (या आंशिक रूप से) स्वयं करके देखें। यह और भी बेहतर होगा यदि आप इसका प्रयास अपने किसी सहयोगी के साथ करें, क्योंकि जब आप अनुभव पर विचार करेंगे तो आपको मदद मिलेगी। स्वयं प्रयास करने से आपको शिक्षार्थी के अनुभवों के भीतर झांकने का मौका मिलेगा, जो परोक्ष रूप से आपके शिक्षण और एक शिक्षक के रूप में आपके अनुभवों को प्रभावित करेगा। जब आप तैयार हों, तो अपने विद्यार्थियों के साथ गतिविधियों का उपयोग करें। पाठ के बाद, इस बात पर विचार करें कि गतिविधि कैसी हुई और उससे क्या सीख मिली। इससे आपको सीखने वाले विद्यार्थियों पर ध्यान केंद्रित रखने वाला अधिक शैक्षिक वातावरण बनाने में मदद मिलेगी।
गतिविधि 1: स्थापित और स्वीकृत तथ्यों की एक उपयोगी सूची बनाना
अपने विद्यार्थियों को यह बताएँ कि तालिका 1 में ऐसे कुछ स्थापित और स्वीकृत कथनों की सूची दी गई है, जो विद्यालय के गणित में उपयोगी होते हैं। ध्यान दें कि पहली पाँच पंक्तियाँ ज्यामिति के पिता कहे जाने वाले प्राचीन यूनान के प्रसिद्ध गणितज्ञ यूक्लिड के ’सामान्य मतों’ से लिए गए हैं, जो उनकी पुस्तक तत्व में दिए गए हैं।
| स्थापित या स्वीकृत कथन या तथ्य | एक उदाहरण लिखें या बनाएँ | जब मुझे यह पता चलता है, तो मुझे वह भी पता चल जाता है–... |
|---|---|---|
| ऐसी चीज़ें जो समान चीज़ों के बराबर होती हैं, वे एक–दूसरे के भी बराबर होती हैं (समतुल्यता का सकर्मक गुणधर्म) | ||
| जब समान चीज़ों को समान चीज़ों में जोड़ा जाता है, तो परिणाम भी समान होते हैं | 7 + 3 = 4 + 6 23 – 4 = 19 – 0 अतः: 7 + 3 + 23 – 4 = 4 + 6 + 19 - 0 | |
| जब समान चीज़ों को समान चीज़ों में से घटाया जाता है, तो शेषफल समान होता है | ||
| पूर्ण संख्या अपने किसी भी भाग से बड़ी होती है | ||
| किसी भी बिंदु पर कोणों का योग 360° होता है | 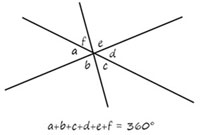 | सरल रेखा का कोण 180° होता है |
| जब कोई रेखा कई समांतर रेखाओं को काटती (या गुजरती) है, तो लंबवत रूप से विपरीत कोण बराबर होते हैं और संगत कोण बराबर होते हैं | 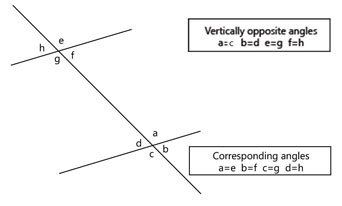 | एकांतर कोण बराबर होते हैं |
| यदि दो रेखाएँ एक–दूसरे को काटती हैं, तो लंबवत रूप से विपरीत कोण बराबर होते हैं | ||
अपने विद्यार्थियों से निम्न प्रश्न पूछें:
- क्या आप इनमें से किसी को पहचानते हैं? उनका जो मतलब हो सकता है क्या आप ऐसा चित्र बना सकते हैं?
क्या आप ऐसे अन्य स्थापित और स्वीकृत कथन जानते हैं, जिन्हें इस सूची में जोड़ा जा सकता है?
कथनों को पुनः देखें और सोचें: ‘जब मुझे यह पता चलता है, तो मुझे वह भी पता चल जाता है ... इन्हें लिख लें। आप अब स्वयं के गणितीय कथनों की खोज कर रहे हैं!
- अपने साथी से अपने काम और अपनी सोच की चर्चा करें, और उन्हें विश्वास दिलाने का प्रयास करें कि आप सही हैं!
गतिविधि 2: यह सिद्ध करना कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है
अपने विद्यार्थियों को बताएँ कि समांतर रेखाओं को काटने वाली रेखा के कोणों संबंधी तथ्य इस बात को सिद्ध कर सकते हैं कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है।
(इस गतिविधि के लिए केस स्टडी 1 को पढ़ना आपके विद्यार्थियों के लिए मददगार हो सकता है।)
अब अपने विद्यार्थियों को बताएँ:
ऐसे सभी साक्ष्यों को साथ में रखें। अपने विचार में मदद लेने के लिए वाक्य ‘जब मुझे यह पता चलता है, तो मुझे वह भी पता चल जाता है ...’ का उपयोग करें।
- अपने साथी से अपने काम और अपनी सोच की चर्चा करें, और उन्हें विश्वास दिलाने का प्रयास करें कि आप सही हैं!
केस स्टडी 2: श्रीमती अग्रवाल गतिविधि 1 और 2 के उपयोग के बारे में बताती हैं
यह एक अध्यापिका की कहानी है, जिसने अपने माध्यमिक कक्षा के विद्यार्थियों के साथ गतिविधि 1 और 2 को आजमाया।
चूँकि विद्यार्थियों के पास काम करने के लिए कुछ उदाहरण थे, इसलिए उन्हें यह आरेखित करने में प्रसन्नता हुई कि कथनों का क्या मतलब हो सकता है। उन्हें यूक्लिड के सामान्य मतों को समझने में थोड़ी परेशानी हुई और इससे एक रोचक चर्चा निकली कि जिस गणितीय भाषा के संपर्क में आए, वह तुलना में इतनी अस्पष्ट नहीं थी!
रानू ने पूछा कि ‘∠A = 30° और ∠A = ∠B तो ∠B = 30°’ जैसा कुछ ’ऐसी चीज़ें, जो समान चीज़ों के बराबर होती हैं, वे एक–दूसरे के भी बराबर होती हैं’ कथन के लिए सही माना जा सकता है। मैंने इसपर स्वीकृति या अस्वीकृति नहीं दी, क्योंकि मैं चाहती थी कि रानू यह तय करे कि क्या यह सही होगा। मैंने उसे दुहराते हुए उत्तर दिया, जो कार्य में इसने कहा थाः
’जब आपको यह पता चलेगा, तो आपको और क्या पता चलेगा?’
- ’प्रयास करें और अपने साथी को विश्वास दिलाएँ कि आप सही हैं।’
गतिविधि 2 के लिए मैंने सुझाई गई विधि का उपयोग किया। सबसे पहले मैंने उनके सामने श्रीमती कपूर की कक्षा का केस स्टडी जोर से पढ़ा; फिर मैंने चिंतन के विचार से प्रश्न पूछेः ’कक्षा, क्या आपको लगता है – क्या आपको यकीन है कि ये विचार गणितीय प्रमाण हैं? क्या प्रधानमंत्री को विश्वास होगा? क्या उन्हें विश्वास होना चाहिए?’ ऐसा करने के पीछे मेरे कारण यह थे कि यदि मैं उनसे कहती कि सिद्ध करो कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है, तो वे उन्हीं प्रमाणों को गिनाते जो श्रीमती कपूर की कक्षा के बच्चों ने बताए थे और मैं यह बताते हुए शुरू करना चाहती थी कि इन्हें प्रमाण नहीं माना जा सकता। अधिकांश बच्चे पहले इस बात से सहमत थे कि श्रीमती कपूर के विद्यार्थियों ने जो बताया था, वे विश्वास दिलाने वाले प्रमाण थे, लेकिन कुछ विद्यार्थी आश्वस्त नहीं थे। मैंने उनसे पूछा कि ऐसा क्यों, तो उन्होंने कहा कि उन्हें यह विश्वास नहीं है कि ये प्रमाण स्थापित या स्वीकृत तथ्यों पर आधारित हैं। इससे अनुभवसिद्ध साक्ष्य के बारे में चर्चा निकली, यह क्या थे और इन्हें गणितीय प्रमाण क्यों नहीं माना गया।
उसके बाद ही मैंने गतिविधि 2 बताई और विद्यार्थियों को इसके साथ खेलने, चीज़ें आजमाने और परीक्षण करने को कहा। इससे वे सहज हुए और उन्होंने अपने विचारों पर चर्चा करके और अपने तर्कों को अपने पड़ोसियों के साथ आजमाकर खुशी–खुशी इस पर काम किया। बाद में, हमने उनके विचारों पर पूरी कक्षा के साथ चर्चा की। कुछ प्रमाणों पर पूरी कक्षा को विश्वास नहीं हुआ, लेकिन कई विद्यार्थियों ने अपने प्रमाण के लिए ठोस आधार तैयार किया था।
मुझे कुछ ऑनलाइन वीडियो भी मिले, जिनमें प्रमाण दिखाई देता है, जैसे खान एकेडमी द्वारा तैयार वीडियो {नीचे ‘अतिरिक्त संसाधन’ देखें}। यद्यपि मैं इन्हें कक्षा में दिखा न सकी, लेकिन मैंने विद्यार्थियों को इनके बारे में बताया, ताकि उन्हें इनकी जानकारी रहे।
अपने शिक्षण अभ्यास में दिखाना
जब आप अपनी कक्षा के साथ ऐसा कोई अभ्यास करें, तो बाद में बताएं कि क्या ठीक रहा और कहां गड़बड़ हुई। ऐसे सवाल की ओर ध्यान दें, जिसमें विद्यार्थियों की रुचि दिखाई दी हो और वे काम कर पाए और वे जिनका आपको स्पष्टीकरण करने की आवश्यकता हुई। ऐसी बातें ऐसी ’स्क्रिप्ट’ पता करने में सहायक होती हैं, जिससे आप विद्यार्थियों को शामिल कर सकें और विद्यार्थी गणित को रुचिकर और आनंददायक पा सकें। यदि वे कुछ भी समझ नहीं पाते हैं तथा कुछ भी नहीं कर पाते हैं, तो वे शामिल होने में कम रुचि लेंगे। जब भी आप गतिविधियां करें, इस चितंन पर आधारित अभ्यास का उपयोग करें, इस बात पर ध्यान देते हुए, जैसे श्रीमती कपूर ने किया था, कि कुछ छोटी–छोटी चीज़ों से काफी फर्क पड़ा।
विचार के लिए रुकें ऐसे चिंतन को गति देने वाले अच्छे सवाल हैं:
|
4 गणितीय गुणधर्मों के बारे में विद्यार्थियों को सोचने में मदद करने वाली कार्य डिजाइन
गतिविधि 2 में, विद्यार्थियों ने निगमन विचार के लिए अपनी प्राकृतिक शक्तियों के आधार पर और गणितीय गुणधर्मों के अपने ज्ञान का उपयोग करके अपनी स्वयं की गणितीय ’सत्यताओं’ का निर्माण किया। गणितीय गुणधर्मों के बारे में जानकारी होना बहुत महत्वपूर्ण है, क्योंकि गणितीय प्रमाण में कोई भी तर्क इनपर आधारित होना चाहिए। इसी प्रकार, जब कोई कथन लागू होता है और जब लागू नहीं होता, इस बारे में गणितीय स्थितियों को परिभाषित करना भी समान महत्वपूर्ण होता है।
गणितीय समुच्चयों के लिए गुणधर्म और स्थितियाँ परिभाषित करने के बारे में विद्यार्थियों को अवगत होने में सहायता करने के लिए क्रमण और वर्गीकरण के कार्य प्रभावी होते हैं; अर्थात यह कि कौन से गुणधर्म कौन से समुच्चय के हैं। क्रम से छाँटने और वर्गीकरण द्वारा आप भिन्नताओं और समानताओं के बारे में सोचते हैं। अगली गतिविधि में इस तरीके का उपयोग किया गया है।
गतिविधि 3: गुणधर्म और स्थितियाँ पता करने के लिए क्रम से छाँटना और वर्गीकरण
अपने विद्यार्थियों को बताएँ कि ’समानुपात’ उन अनुपातों का एक युग्म है, जो बराबर होते हैं। आनुपातिक होना एक ऐसा गुणधर्म है, जो गणित में विभिन्न विषयों और अवधारणाओं में अक्सर दिखाई देता है।
नीचे आने वाले कथन कुछ ऐसे परिदृश्यों का वर्णन करते हैं, जो गणितीय अवधारणाओं के बारे में बताते हैं। अपने विद्यार्थियों से कहें कि इन्हें पढ़ें और वर्गीकृत करें कि क्या वे आनुपातिक होंगे या नहीं, और किन स्थितियों में होंगे। उन्हें अपने कारण प्रदान करना चाहिए और किसी मित्र को विस्तार से बताना चाहिए कि उदाहरण किसके अनुपाती होगा (या नहीं होगा)। आलोचनात्मक बनें!
- a.किसी फोटोग्राफ को बड़ा करना।
- b.सैंडविच बनाने के लिए ब्रेड के स्लाइस काटना।
- c.एक चर में किसी रैखिक समीकरण का समीकरण (ax + b = 0)।
- d.किसी दी गई समयसीमा में लोगों की किसी संख्या द्वारा किया गया काम।
- e.किसी विशेष सिनेमा में किसी विशेष फिल्म को देखने के लिए लोगों की किसी संख्या द्वारा व्यय की गई राशि।
- f.ट्रेन की यात्राओं में टिकट का किराया।
- g.किसी रेखाखंड को m समान भागों में विभाजित करना।
- h.कुतुब मीनार की ऊँचाई (चित्र 1)।
चित्र 1 कुतुब मीनार, दिल्ली।
- i.किसी वृत्त का क्षेत्रफल।
- j.किसी वर्ग का क्षेत्रफल।
- k.किसी बेलन की ऊँचाई और इसकी त्रिज्या का गुणनफल।
- l.किसी शंकु का आयतन।
- m.किसी रिक्शा का किराया।
केस स्टडी 3: गतिविधि 3 के उपयोग का अनुभव श्रीमती अग्रवाल बताती हैं
विद्यार्थियों की इस गतिविधि से जुड़ने में मदद करने के लिए, हमने कक्षा में निर्देशों और उदाहरणों (a) और (b) को साथ में जोर से पढ़ा। फिर हमने (a) के लिए संभावित उत्तरों के बारे में विचार मंथन किया, और फिर उन स्थितियों की चर्चा की, जिन्हें बड़ी की गई फोटोग्राफ को पुरानी वाली के अनुपात में रखने के लिए पूरा करने की आवश्यकता होगी। इसे राहुल द्वारा शुरू किया गया था, जिसने कहा कि फोटोग्राफ को दोगुना बड़ा करने के लिए आपको इसकी चौड़ाई को दोगुना करना होगा। मैं देख सकती थी कि उषा सोच रही थी, क्योंकि उसकी भौंहें चढ़ी हुई थी, और फिर उसने कहा कि इससे काम नहीं होगा क्योंकि इससे चित्र बेडौल दिखाई देगा।
मैंने फिर विद्यार्थियों से कहा कि वे उदाहरणों पर अलग–अलग काम करें ताकि वे पहले अपने स्वयं के विचार और सोच तैयार कर सके, और फिर उनसे अपनी सोच और विचार की चर्चा अपने साथी से करने को कहा।
कुछ समय बाद, मैंने पूरी कक्षा से चर्चा के लिए और विद्यार्थियों के लिए उनके विचार साझा करने के लिए कुछ कथन चुनें। मैंने देखा कि विद्यार्थी बार–बार कुछ ऐसे वाक्य उपयोग कर रहे थेः
- ’लेकिन क्या होगा यदि...?’
- ’यदि आप इसे बदलते हैं, तो उससे यह बदल जाता है/फिर भी वैसा ही रहता है।’
- ’यह समान है, यह अलग है।’
मैंने विद्यार्थियों को ध्यान दिलाया और उन्होंने भी सहमति दी कि गणितीय गुणधर्मों और शर्तों के बारे में पता लगाने के लिए ये अच्छे वाक्य हैं। दो विद्यार्थियों ने झट से एक बड़े कागज पर इन वाक्यों को लिख लिया और उसे शीर्षक दिया कि ’गणितीय गुणधर्मों और शर्तों के बारे में पता लगाने के लिए अच्छे वाक्य’, और फिर कागज को दीवार पर चिपका दिया।
विचार के लिए रुकें
|
5 विश्वास दिलाने के लिए शिक्षण
तर्क–वितर्क और निगमन के औपचारिक नियम जिनका उपयोग गणितीय प्रमाण में किया जाता है, उन्हें विद्यालय स्तर पर सिखाना आसान नहीं है। प्रयुक्त भाषा एकदम अलग होती है और अवधारणाओं को अक्सर विद्यार्थियों के अनुभव की दुनिया से परे माना जाता है। कुछ हद तक यह आश्चर्यजनक है, क्योंकि विचार और निगमन ऐसा कौशल और शक्तियाँ हैं जो हम सभी के पास होती हैं, साथ ही विश्वास दिलाने के विभिन्न स्तरों के बारे में जानना, जो कि कठिन है।
अगली दो गतिविधियों का लक्ष्य विद्यार्थियों के उन कौशलों और अनुभवों का उपयोग करना है, जो उनके पास अपने विचारों को अधिक व्यवस्थित और औपचारिक बनाने के लिए हर दिन के विचारों से आते हैं। इस तरह से यह उन बातों पर आधारित होता है, जो विद्यार्थी पहले से जानते हैं और करते हैं। पहली वाली में यह पता करने के लिए कि क्या कथन मान्य है और कब मान्य है, ’हमेशा सत्य, कभी कभार सत्य या कभी सत्य नहीं’ के कार्य डिजाइन का उपयोग किया जाता है।
फिर इस गतिविधि के परिणामों का उपयोग अगली वाली में किया जाता है, जहाँ विद्यार्थी अपने विचार और तर्क–वितर्क में कठिनाई के भिन्न स्तरों पर काम करते हैं। यहाँ पर कार्य डिजाइन ’स्वयं को विश्वास दिलाएँ, मित्र को विश्वास दिलाएँ, रामानुजन को विश्वास दिलाएँ’ की विधि का उपयोग करती है।
जिन लोगों को विश्वास दिलाना है, उन्हें अलग करने से विद्यार्थियों को अधिक सटीक बनने में मदद मिलती है। स्वयं को विश्वास दिलाना अक्सर आसान होता हैः आप अनुभवसिद्ध साक्ष्य से खुश हो सकते हैं और प्रयुक्त भाषा ढीली और अस्पष्ट हो सकती है, क्योंकि इसकी जोर से व्याख्या करने की कोई आवश्यकता नहीं है। किसी मित्र को विश्वास दिलाने के लिए भाषा में अधिक सटीकता की आवश्यकता होती है, क्योंकि विचार को संचार और प्रयुक्त तर्कों की वैधता के लिए सुव्यवस्थित और शब्दों में व्यक्त होना चाहिए। हालाँकि आपका मित्र आपकी बात को अभी भी स्वीकार करने को इच्छुक हो सकता है, क्योंकि वे आपके मित्र हैं, यद्यपि वे आपको स्वयं से अधिक चुनौती दे सकते हैं। महान भारतीय गणितज्ञ रामानुजन को विश्वास दिलाने के लिए ठोस गणितीय औचित्य की आवश्यकता होगी, क्योंकि वे अपने तर्क–वितर्क से कमियाँ निकालने का प्रयास करेंगे। रामानुजन को विश्वास दिलाने के लिए तर्कों को स्वीकृत और स्थापित गणितीय कथनों पर आधारित होना चाहिए, क्योंकि केवल वही अविवादित हैं।
गतिविधि 4: हमेशा सत्य, कभी–कभी सत्य या कभी भी सत्य नहीं
तैयारी
नीचे दिए गए कथनों के लिए विद्यार्थियों के पास इन विषयों के बारे में कुछ ज्ञान होना आवश्यक है। उनको चुनें, जो आपकी कक्षा के लिए प्रासंगिक हों।
गतिवधि
अपने विद्यार्थियों को निम्न बताएँ:
- निम्न कथनों को पढ़ें। इनमें से कौन से हमेशा सत्य हैं, कभी–कभी सत्य हैं या कभी भी सत्य नहीं हैं? अपने साथी से अपने कारणों की चर्चा करें।
a.यदि p एक अभाज्य संख्या है, तो p + 1 एक संयुक्त संख्या होगी।
b.वृत्त की N जीवाएँ वृत्तीय क्षेत्र को N + 1 अनाच्छादित भागों में विभाजित करती है।
- c.यदि दो गोलों का आयतन समान है, तो वे गोले सर्वांगसम होंगे।
- d.किसी त्रिभुज का केंद्रक त्रिभुज के भीतर होता है।
- e.अभाज्य संख्याएँ अनंत होती हैं।
- अपने स्वयं के कुछ और कथन बनाएँ और उन्हें अपने साथी को दें। इनमें से कौन से हमेशा सत्य हैं, कभी–कभी सत्य हैं या कभी भी सत्य नहीं हैं?
गतिविधि 5: स्वयं को विश्वास दिलाएँ, अपने मित्र को विश्वास दिलाएँ, रामानुजन को विश्वास दिलाएँ
अपने विद्यार्थियों से कहें:
याद रखें कि रामानुजन आपके कारणों में कमियाँ निकालने का प्रयास करेगा।
- गतिविधि 4 को फिर से करें, लेकिन अपने साथी से अपने कारणों की केवल चर्चा करने के बजाए अब आपको औचित्य भी बताना होगा जोः
- आपको स्वयं को विश्वास दिलाए
- मित्र को विश्वास दिलाए
- रामानुजन को विश्वास दिलाए।
- कक्षा के साथ आपका सबसे अधिक विश्वास दिलाने वाला औचित्य साझा करें। क्या अन्य विद्यार्थी आपके तर्कों से सहमत हैं?
केस स्टडी 4: श्रीमती आशा गतिविधि 4 और 5 के उपयोग पर अपने अनुभव बताती हैं
मैंने गतिविधि 4 – इस बात पर चर्चा कि कोई कथन हमेशा, कभी–कभी सत्य होता है या कभी सत्य नहीं होता – को विद्यार्थियों को तीन और चार के समूहों में बाँटकर करने का निर्णय किया, क्योंकि मैंने सोचा कि इससे उन्हें और विचार एकत्र करने का अवसर मिलेगा। मैंने देखा कि इस स्थिति में तीन के समूहों ने बेहतर काम किया – वे एक–दूसरे के साथ अधिक जुड़े हुए थे – जबकि चार विद्यार्थियों के समूह में कुछ जुड़े हुए नहीं थे और केवल सुन रहे थे। गतिविधि 5 के लिए, मैंने उन्हें युग्म में काम करने को कहा ताकि हर बच्चे को अपना औचित्य बताने का अवसर और समय मिले। इन कामों के बारे में एक अच्छी बात यह है कि ये विद्यार्थियों को अपनी राय देने और औचित्य बताने के लिए बाध्य करते हैं, भले ही पहले वे केवल सुनने का ही काम कर रहे थे।
जब मैंने विद्यार्थियों से पूछा कि क्या स्वयं को, मित्र को, या रामानुजन को विश्वास दिलाते समय उनके तर्कों में कोई अंतर था, तो उन्होंने कहा कि कुछ स्थितियों में उन्हें अधिक सटीक और समग्र बनने की आवश्यकता हुई। हालाँकि कुछ अन्य स्थितियों में विद्यार्थियों ने महसूस किया कि वे अपने तर्क में कारण नहीं बता पाए क्योंकि उन्हें कोई कारण सूझा ही नहीं – उन्हें बस इतना पता था कि कथन सही है, क्योंकि मैंने पहले उन्हें यह बताया था! तार्किक प्रमाण तैयार करने में मदद कर सकने वाले चरण सोचने में मदद करने के लिए मैंने सोचा कि कक्षा में किसी के पास कोई सुझाव होगा और हो सकता है कि मेरे बजाय कोई विद्यार्थी इसे साझा करे तो वे अधिक आलोचनात्मक रूप से पेश आएँगे। मैंने समूहों से वे कथन बताने को कहा जिनके साथ यह हुआ था और अन्य विद्यार्थियों पूछा कि क्या उन्होंने कोई औचित्य बताया था। औचित्य को पूरी कक्षा को समझाया गया और मैंने सभी विद्यार्थियों से कहा कि औचित्य में उसी तरह कमियाँ निकालें जिस तरह कोई असली गणितज्ञ करता है। इसके बाद मैं उन विद्यार्थियों के पास वापस गई जो अटक गए थे और उन्होंने बताया कि चर्चा से उन्हें अपनी उलझन से निकलने में मदद मिली।
अपनी कक्षा में शिक्षण के लिए प्रश्नोत्तरी और बातचीत का उपयोग करने के बारे में अधिक जानकारी के लि, संसाधन 2 और 3 देखें।
विचार के लिए रुकें
|
6 सारांश
गणित के शिक्षण, विशेष रूप से प्रमाण के बारे में, अक्सर विद्यार्थियों द्वारा पूरे तथ्यों और प्रक्रियाओं को जानने और याद करने के रूप में देखा जाता है। विद्यार्थियों को गणितीय कारण समझाना अक्सर न केवल उन्हें स्वयं के लिए गणितीय ’सत्यता’ का निर्माण करने में सक्षम बनाता है, बल्कि उन्हें गणित को समझने में भी मदद करता है। गणितीय कारण बताने के लिए उन्हें अपने तर्क तैयार करने के लिए गणितीय गुणधर्मों को खोजना और उपयोग करना होगा। इस तरह से गणितीय कारण तैयार करने को अक्सर विषय की खूबसूरती माना जाता है, और निश्चित रूप से यह विषय की एक मुख्य अवधारणा है। प्रमाण पर अपने विद्यार्थियों के साथ काम करके आप उन्हें एक गणितज्ञ की भूमिका निभाने और मनोहारी गणित की सराहना करने के लिए आमंत्रित कर रहे हैं।
विचार के लिए रुकें इस इकाई में आपके द्वारा उपयोग किए गए तीन विचार पहचानें जो अन्य विषयों को पढ़ाने में भी काम करेंगे। ऐसे दो विषय लिखें, जिन्हें आप शीघ्र ही पढ़ाने वाले हैं और जहाँ पर थोड़े–बहुत फेरबदल के साथ उन विचारों का उपयोग किया जा सकता है। |
संसाधन
संसाधन 1: एनसीएफ/एनसीएफटीई शिक्षण आवश्यकताएँ
यह यूनिट NCF (2005) तथा NCFTE (2009) की निम्न शिक्षण आवश्यकताओं से जोड़ता है तथा उन आवश्यकताओं को पूरा करने में आपकी मदद करेगाः
शिक्षार्थियों को उनके शिक्षण में सक्रिय प्रतिभागी के रूप में देखें न कि सिर्फ ज्ञान प्राप्त करने वाले के रूप में; ज्ञान निर्माण के लिए उनकी क्षमताओं को प्रोत्साहित करने के लिए; रटने की पद्धतियों से शिक्षण को दूर ले जाने के लिए।
- शिक्षण को निजी अनुभवों से अर्थ की खोज के रूप में और ज्ञान निर्माण को विचारात्मक शिक्षण की निरंतर विकास प्रक्रिया के रूप में देखें।
- विद्यार्थियों को गणित को किसी ऐसी चीज़ के रूप में लेने दें जिसके बारे में वे बात करें, जिसके द्वारा संवाद करें, जिसकी आपस में चर्चा करें, जिसपर साथ मिलकर कार्य करें।
संसाधन 2: चिंतन को बढ़ावा देने के लिए प्रश्न पूछने का उपयोग करना
शिक्षक हमेशा अपने विद्यार्थियों से प्रश्न पूछते हैं; प्रश्नों के माध्यम से शिक्षक अपने विद्यार्थियों की सीखने, अधिक सीखने में मदद कर सकते हैं। एक अध्ययन के अनुसार औसत रूप से, एक शिक्षक विद्यार्थियों से प्रश्न पूछने में अपना एक–तिहाई समय देता है (हेस्टिंग्ज, 2003)। पूछे गए प्रश्नों में, 60 प्रतिशत में तथ्यों की याद दिलाई गई और 20 प्रतिशत प्रक्रिया से संबंधित थे (हैटी, 2012), जिनमें अधिकांश के उत्तर सही या गलत होते थे। लेकिन क्या ऐसे सवाल पूछने से, जिनके जवाब सही या गलत होते हैं, शिक्षण को बढ़ावा मिलता है?
ऐसे कई प्रकार के प्रश्न हो सकते हैं, जो विद्यार्थी पूछ सकते हैं। शिक्षक जो जवाब और परिणाम चाहता है, उससे प्रश्न का वह प्रकार पता चलता है, जिसे शिक्षक को उपयोग करना चाहिए। शिक्षक अक्सर इसलिए विद्यार्थियों से प्रश्न पूछते हैं:
- नया विषय या सामग्री आने पर विद्यार्थियों को समझने के लिए विषयवस्तु के प्रस्तुतीकरण के लिए
- विद्यार्थियों को अपनी सोच का अधिक से अधिक भाग साझा करने हेतु प्रेरित करने के लिए
- गलती से बचाने के लिए
- विद्यार्थियों को आगे बढ़ाने के लिए
- समझ की जाँच करने के लिए।
सामान्य तौर पर प्रश्न यह जानने के लिए पूछे जाते हैं कि विद्यार्थी क्या जानते हैं, इसलिए उनकी प्रगति के आंकलन के लिए यह महत्वपूर्ण है। प्रश्नों का उपयोग विद्यार्थियों को प्रेरित करने, उनका चिंतन कौशल बढ़ाने और जिज्ञासु प्रवृत्ति का विकास करने के लिए भी किया जाता है। उन्हें दो मुख्य श्रेणियों में विभाजित किया जा सकता हैः
निचले स्तर के प्रश्न, जिनसे कि तथ्यों का स्मरण और पहले सिखाया गया ज्ञान जुड़ा होता है, प्रायः बंद सिरे के प्रश्नों (हां या नहीं में उत्तर) से संबद्ध होते हैं।
- उच्च स्तरीय प्रश्न, जिनमें अधिक चिंतन की आवश्यकता होती है। वे कोई उत्तर बनाने या किसी दलील का तार्किक रूप से समर्थन करने के लिए विद्यार्थियों से पहले प्राप्त की गई जानकारी को एक साथ रखने को कह सकते हैं। उच्च स्तर के प्रश्न प्रायः ज्यादा खुले सिरों वाले होते हैं।
खुले सिरों वाले (प्रश्न से नये प्रश्न उत्पन्न हों) प्रश्न विद्यार्थियों को पाठ्यपुस्तक आधारित, शब्दशः उत्तरों से परे सोचने को प्रेरित करते हैं, जिससे कई तरह के उत्तर मिलते हैं। वे सामग्री के बारे में विद्यार्थियों की समझ का आंकलन करने में भी शिक्षकों की मदद करते हैं।
विद्यार्थियों को उत्तर देने के लिए प्रोत्साहित करने वाले
कई शिक्षक किसी प्रश्न का उत्तर देने के लिए एक सेकंड से भी कम का समय देते हैं और इसलिए उन्हें स्वयं प्रश्न का उत्तर देना पड़ता है या प्रश्न का रूप बदलना पड़ता है (हेस्टिंग्ज, 2003)। विद्यार्थियों के पास केवल उत्तर देने का समय होता है – सोचने का नहीं! अगर आप कुछ सेकंड इंतजार करते हैं तो विद्यार्थियों को उत्तरों के बारे में सोचने के लिए समय मिल जाता है। इसका विद्यार्थियों की उपलब्धि पर सकारात्मक प्रभाव पड़ता है। प्रश्न को प्रस्तुत करने के बाद इंतजार करने से निम्न में वृद्धि होती हैः
- विद्यार्थियों के उत्तरों की लंबाई
- उत्तर देने वाले विद्यार्थियों की संख्या
- विद्यार्थियों के प्रश्नों की बारंबारता
- कम सक्षम विद्यार्थियों के पास से उत्तरों की संख्या
- विद्यार्थियों के बीच सकारात्मक संवाद।
आपका उत्तर महत्व रखता है
दिए गए सभी उत्तरों को जितनी सकारात्मकता से आप प्राप्त करते हैं, उतने अधिक विद्यार्थी सोचना और प्रयास करना जारी रखेंगे। यह सुनिश्चित करने के कई तरीके हैं कि गलत उत्तर और गलत अवधारणाओं को सही किया जाता है, और यदि एक विद्यार्थी का विचार गलत होता है तो आप यह मान सकते हैं कि अन्य लोगों के विचार भी ऐसे ही होंगे। आप निम्न आज़मा सकते हैं:
- आप उत्तरों के उन हिस्सों को चुन सकते हैं, जो कि सही हैं और सहायक ढंग से विद्यार्थी से अपने उत्तर के बारे में थोड़ा और सोचने के लिए कह सकते हैं। यह ज्यादा सक्रिय भागीदारी को प्रोत्साहित करता है और आपके विद्यार्थियों की अपनी गल्तियों से सीखने में मदद करता है। निम्नलिखित टिप्पणी यह दर्शाती है कि आप ज्यादा मददगार ढंग से किस प्रकार से गलत उत्तर पर प्रतिक्रिया दे सकते हैं: ”आप वाष्पीकरण से बनते बादलों के बारे में सही थे, लेकिन मुझे लगता है कि हमें बारिश के बारे में आपने जो कहा है, उसके बारे में थोड़ा और पता लगाने की जरूरत है। क्या किसी और के पास कोई विचार है?’
विद्यार्थियों द्वारा दिए जाने वाले सभी उत्तरों को ब्लैकबोर्ड पर लिख लें, और फिर विद्यार्थियों से उन सभी के बारे में सोचने को कहें। कौन से उत्तर उन्हें सही लगे? किन बातों से और जवाब निकलकर आए? यह आपको यह समझने का अवसर देता है कि आपके विद्यार्थी किस तरह सोच रहे हैं और आपके विद्यार्थियों को उनकी गलत धारणाओं को बिना डरे सही करने का तरीका भी देता है।
सभी उत्तरों को ध्यानपूर्वक सुनकर और विद्यार्थी को और विस्तार से बताने को कहकर उनका सम्मान करें। यदि आप सभी उत्तरों के लिए अधिक विस्तार माँगते हैं, चाहे वह सही हो या गलत, तो विद्यार्थी अपनी गलतियाँ खुद ही सही कर लेंगे; इस तरह से आप एक विचारशील कक्षा का निर्माण करेंगे और आपको वास्तव में पता चलेगा कि आपके विद्यार्थियों ने क्या किया है और आगे कैसे बढ़ना है। यदि गलत उत्तरों पर डाँटा या सजा दी जाती है, तो फिर आपके विद्यार्थी हँसाई या शर्मिंदगी के डर से प्रयास करना बंद कर देंगे।
उत्तरों की गुणवत्ता को बेहतर बनाना
यह महत्वपूर्ण है कि आप प्रश्नों का एक ऐसा क्रम अपनाने का प्रयास करें जो सही उत्तर पर समाप्त न होता हो। सही उत्तर के पुरस्कारस्वरूप अनुवर्ती प्रश्न पूछा जाना चाहिए, जो ज्ञान बढ़ाए और विद्यार्थियों को शिक्षक के साथ जुड़ने का अवसर प्रदान करे। आप यह पूछकर ऐसा कर सकते हैं:
- कैसे या क्यों
- उत्तर देने का दूसरा तरीका
- बेहतर शब्द
- उत्तर को प्रमाणित करने का साक्ष्य
- संबंधित कौशल का एकीकरण
नई सेटिंग में उसी कौशल या तर्क का अनुप्रयोग।
विद्यार्थियों की उनके उत्तर के बारे में ज्यादा गहराई में जाकर सोचने में मदद करना (और उनकी गुणवत्ता को बेहतर बनाना) आपकी भूमिका का बहुत ही महत्वपूर्ण हिस्सा है। निम्न कौशल विद्यार्थियों को अधिक प्राप्त करने में मदद करेंगेः
- प्रेरण में उपयुक्त संकेत दिए जाने चाहिए – ऐसे जो विद्यार्थियों की उनके उत्तरों को तैयार करने और बेहतर बनाने में मदद करें। उत्तर में सही क्या है इसे पहले बताना चुनकर बोलना शुरू कर सकते हैं और बाद में जानकारी, आगे के प्रश्न तथा अन्य संकेत दे सकते हैं। (‘तो अगर आप कागज के अपने हवाई जहाज के आखिर में वजन रखते हैं तो क्या होगा?’)
- जांच–पड़ताल, अव्यवस्थित उत्तर या उस उत्तर को जो कि आंशिक रूप से सही है, को बेहतर बनाने के लिए और अधिक का पता लगाने की कोशिश करना, विद्यार्थियों को यह स्पष्ट करना कि वे क्या कहने की कोशिश कर रहे हैं, को कहते हैं। (”तो यह सब साथ में कैसे काम करता है, उसके बारे में आप मुझे और क्या बता सकते हैं?“)
- फिर से ध्यान केंद्रित करना विद्यार्थियों के ज्ञान को उस ज्ञान से जोड़ने के लिए जिसे वे पहले सीख चुके होते हैं, सही उत्तरों के आधार पर निर्माण करना होता है। यह उनकी समझदारी को विकसित करता है। (’जो आपने कहा वह सही है, लेकिन यह उससे किस प्रकार से जुड़ता है, जिस पर कि हम पिछले सप्ताह अपने स्थानीय पर्यावरण के विषय में विचार कर रहे थे?’)
- प्रश्नों का क्रम बनाने का अर्थ सोच–विचार को विस्तारित करने के लिए एक निश्चित क्रम में प्रश्न पूछना होता है। प्रश्नों से विद्यार्थियों को सारांशित करने, तुलना करने, व्याख्या करने या विश्लेषण करने में मदद मिलनी चाहिए। ऐसे प्रश्न तैयार करें जो विद्यार्थियों के दिमाग पर जोर डालें, लेकिन वे इतने भी क्लिष्ट नहीं होने चाहिए कि उससे प्रश्न का अर्थ ही नष्ट हो जाए। (’स्पष्ट करें कि आप अपनी पहले की समस्या से किस प्रकार उबरे। उससे क्या फर्क पड़ा? आपको क्या लगता है आगे आपको किस चीज़ का सामना करने की जरूरत पड़ेगी?’)
धैर्यपूर्वक सुनने से आप न केवल उस उत्तर पर गौर करने में समर्थ होते हैं, जिसकी आप अपेक्षा कर रहे होते हैं, बल्कि इससे आप असाधारण या नवोन्मेषी उत्तरों के प्रति सतर्क भी होते हैं, जिसकी हो सकता है कि आपको अपेक्षा न रही हो। इससे यह भी पता चलता है कि आप विद्यार्थियों की सोच का सम्मान करते हैं और इसलिए उनके द्वारा विचारशील जवाब दिए जाने की संभावना अधिक होगी। इस तरह के उत्तर भ्रंतियों को चिह्नांकित कर सकते हैं, जिन्हें ठीक करने की जरूरत होती है अथवा वे एक नयी पहुंच दर्शा सकते हैं, जिन पर आपने विचार नहीं किया हो। (’मैंने इसके बारे में सोचा नहीं था। आप इस तरह से क्यों सोचते हैं इसके बारे में मुझे और जानकारी दें।’)
एक शिक्षक के रूप में, यदि आप अपने विद्यार्थियों से रोचक और नवोन्मेषी उत्तर पाना चाहते हैं तो आपको ऐसे प्रश्न पूछने होंगे जो प्रेरित करें और चुनौतीपूर्ण हों। आपको उन्हें सोचने का समय देना होगा और आपको आश्चर्य होगा कि आपके विद्यार्थी कितना जानते हैं और उनके शिक्षण में प्रगति करने में आप उनकी मदद कैसे कर सकते हैं।
याद रखें कि प्रश्न पूछना इस बारे में नहीं है कि शिक्षक क्या जानता है, लेकिन इस बारे में है कि विद्यार्थी क्या जानते हैं। यह याद रखना महत्वपूर्ण है कि आपको कभी भी अपने प्रश्नों के उत्तर नहीं देने चाहिए! आखिरकार, यदि विद्यार्थियों को यह मालूम होगा कि कुछ देर की चुप्पी के बाद आप उन्हें उत्तर बता देंगे, तो उत्तर बताने पर उन्हें क्या मिलेगा?
संसाधन 3: सीखने के लिए बातचीत
सीखने के लिए बातचीत क्यों जरूरी है
बातचीत मानव विकास का हिस्सा है, जो सोचने–विचारने, सीखने और विश्व का बोध प्राप्त करने में हमारी मदद करती है। लोग भाषा का इस्तेमाल तार्किक क्षमता, ज्ञान और बोध को विकसित करने के लिए औज़ार के रूप में करते हैं। अतः, विद्यार्थियों को उनके शिक्षण अनुभवों के भाग के रूप में बात करने के लिए प्रोत्साहित करने का अर्थ होगा उनकी शैक्षणिक प्रगति का बढ़ना। सीखे गए विचारों के बारे में बात करने का अर्थ होता हैः
- उन विचारों को परखा गया है
- तार्किक क्षमता विकसित और सुव्यवस्थित है
- जिससे विद्यार्थी अधिक सीखते हैं।
किसी कक्षा में रटा–रटाया दोहराने से लेकर उच्च श्रेणी की चर्चा तक विद्यार्थी वार्तालाप के विभिन्न तरीके होते हैं।
पारंपरिक तौर पर, शिक्षक की बातचीत का दबदबा होता था और वह विद्यार्थियों की बातचीत या विद्यार्थियों के ज्ञान के मुकाबले अधिक मूल्यवान समझी जाती थी। तथापि, पढ़ाई के लिए बातचीत में पाठों का नियोजन शामिल होता है ताकि विद्यार्थी इस ढंग से अधिक बात करें और अधिक सीखें कि शिक्षक विद्यार्थियों के पहले के अनुभव के साथ संबंध कायम करें। यह किसी शिक्षक और उसके विद्यार्थियों के बीच प्रश्न और उत्तर सत्र से कहीं अधिक होता है क्योंकि इसमें विद्यार्थी की अपनी भाषा, विचारों और रुचियों को ज्यादा समय दिया जाता है। हम में से अधिकांश कठिन मुद्दे के बारे में या किसी बात का पता करने के लिए किसी से बात करना चाहते हैं, और अध्यापक बेहद सुनियोजित गतिविधियों से इस सहज–प्रवृत्ति को बढ़ा सकते हैं।
कक्षा में शिक्षण गतिविधियों के लिए बातचीत की योजना बनाना
शिक्षण की गतिविधियों के लिए बातचीत की योजना बनाना महज साक्षरता और शब्दावली के लिए नहीं है, यह गणित एवं विज्ञान के काम तथा अन्य विषयों के नियोजन का हिस्सा भी है। इसे समूची कक्षा में, जोड़ी या सामूहिक कार्य में, आउटडोर गतिविधियों में, भूमिका पर आधारित गतिविधियों में, लेखन, वाचन, प्रायोगिक छानबीन और रचनात्मक कार्य में योजनाबद्ध किया जा सकता है।
यहां तक कि साक्षरता और गणना के सीमित कौशलों वाले नन्हें विद्यार्थी भी उच्चतर श्रेणी के चिंतन कौशलों का प्रदर्शन कर सकते हैं, बशर्ते कि उन्हें दिया जाने वाला कार्य उनके पहले के अनुभव पर आधारित और आनंदप्रद हो। उदाहरण के लिए, विद्यार्थी तस्वीरों, आरेखणों या वास्तविक वस्तुओं से किसी कहानी, पशु या आकृति के बारे में पूर्वानुमान लगा सकते हैं। विद्यार्थी रोलप्ले करते समय कठपुतली या पात्र की समस्याओं के बारे में सुझावों और संभावित समाधानों को सूचीबद्ध कर सकते हैं।
जो कुछ आप विद्यार्थियों को सिखाना चाहते हैं, उसके इर्दगिर्द पाठ की योजना बनायें और इस बारे में सोचें, और साथ ही इस बारे में भी कि आप किस प्रकार की बातचीत को विद्यार्थियों में विकसित होते देखना चाहते हैं। कुछ प्रकार की बातचीत अन्वेषी होती है, उदाहरण के लिएः ’इसके बाद क्या होगा?’, ’क्या हमने इसे पहले देखा है?’, ’यह क्या हो सकता है?’ या ’आप ऐसा क्यों सोचते हैं कि वह यह है?’ कुछ अन्य प्रकार की वार्ताएं ज्यादा विश्लेषणात्मक होती हैं, उदाहरण के लिए विचारों, साक्ष्य या सुझावों का आकलन करना।
इसे रोचक, मज़ेदार और सभी विद्यार्थियों के लिए संवाद में भाग लेना संभव बनाने की कोशिश करें। विद्यार्थियों को उपहास का पात्र बनने या गलत होने के भय के बिना दृष्टिकोणों को व्यक्त करने और विचारों का पता लगाने में सहज होने और सुरक्षित महसूस करने की जरूरत होती है।
विद्यार्थियों की वार्ता को आगे बढ़ाएं
शिक्षण के लिए वार्ता अध्यापकों को निम्न अवसर प्रदान करती हैः
विद्यार्थी जो कहते हैं उसे सुनना
- विद्यार्थियों के विचारों की प्रशंसा करना और उस पर आगे काम करना
- इसे आगे ले जाने के लिए विद्यार्थियों को प्रोत्साहित करना।
सभी उत्तरों को लिखना या उनका औपचारिक आकलन नहीं करना होता है, क्योंकि वार्ता के जरिये विचारों को विकसित करना शिक्षण का महत्वपूर्ण हिस्सा है। आपको उनके शिक्षण को प्रासंगिक बनाने के लिए उनके अनुभवों और विचारों का यथासंभव प्रयोग करना चाहिए। सर्वश्रेष्ठ विद्यार्थी वार्ता अन्वेषी होती है, जिसका अर्थ होता है कि विद्यार्थी एक दूसरे के विचारों की जांच करते हैं और चुनौती पेश करते हैं ताकि वे अपने प्रत्युत्तरों को लेकर विश्वस्त हो सकें। एक साथ बातचीत करने वाले समूहों को किसी के भी द्वारा दिए गए उत्तर को स्वीकार करने के लिए प्रोत्साहित नहीं किया जाना चाहिए। आप समूची कक्षा की सेटिंग में ‘क्यों?’, ‘आपने उसका निर्णय क्यों किया?’ या ‘क्या आपको उस हल में कोई समस्या नजर आती है?’ जैसे जांच वाले प्रश्नों के अपने प्रयोग के माध्यम से चुनौतीपूर्ण विचारशीलता को तैयार कर सकते हैं। आप विद्यार्थी समूहों को सुनते हुए कक्षा में घूम सकते हैं और ऐसे प्रश्न पूछकर उनकी विचारशीलता को बढ़ा सकते हैं।
अगर विद्यार्थियों की वार्ता, विचारों और अनुभवों की कद्र और सराहना की जाती है तो वे प्रोत्साहित होंगे। बातचीत करने के दौरान अपने व्यवहार, सावधानी से सुनने, एक दूसरे से प्रश्न पूछने, और बाधा न डालना सीखने के लिए अपने विद्यार्थियों की प्रशंसा करें। कक्षा में कमजोर बच्चों के बारे में सावधान रहें और उन्हें भी शामिल किया जाना सुनिश्चित करने के तरीकों पर विचार करें। कामकाज के ऐसे तरीकों को स्थापित करने में थोड़ा समय लग सकता है, जो सभी विद्यार्थियों को पूरी तरह से भाग लेने की सुविधा प्रदान करते हों।
विद्यार्थियों को खुद से प्रश्न पूछने के लिए प्रोत्साहित करें
अपनी कक्षा में ऐसा वातावरण तैयार करें जहां अच्छे चुनौतीपूर्ण प्रश्न पूछे जाते हैं और जहां विद्यार्थियों के विचारों को सम्मान दिया जाता है और उऩकी प्रशंसा की जाती है। विद्यार्थी प्रश्न नहीं पूछेंगे अगर उन्हें उनके साथ किए जाने वाले व्यवहार को लेकर भय होगा या अगर उन्हें लगेगा कि उनके विचारों का मान नहीं किया जाएगा। विद्यार्थियों को प्रश्न पूछने के लिए आमंत्रित करना उनको जिज्ञासा दर्शाने के लिए प्रोत्साहित करता है, उनसे अपने शिक्षण के बार में अलग ढंग से विचार करने के लिए कहता है और उनके नजरिए को समझने में आपकी सहायता करता है।
आप कुछ नियमित समूह या जोड़े में कार्य करने, या शायद ‘विद्यार्थियों के प्रश्न पूछने का समय’ जैसी कोई योजना बना सकते हैं ताकि विद्यार्थी प्रश्न पूछ सकें या स्पष्टीकरण मांग सकें। आपः
अपने पाठ के एक भाग का नामकरण करें ‘यदि कोई प्रश्न हो तो हाथ उठाये।’
- किसी विद्यार्थी को हॉट–सीट पर बैठा सकते हैं और दूसरे विद्यार्थियों को उस विद्यार्थी से प्रश्न पूछने के लिए प्रोत्साहित कर सकते हैं जैसे कि वे पात्र हों, उदाहरणतः पाइथागोरस या मीराबाई
जोड़ों में या छोटे समूहों में ‘मुझे और अधिक बताएं’ खेल खेल सकते हैं
- मूल पूछताछ का अभ्यास करने के लिए विद्यार्थियों को कौन/क्या/कहां/कब/क्यों वाले प्रश्न ग्रिड दे सकते हैं
विद्यार्थियों को कुछ डेटा (जैसे कि विश्व डेटा बैंक से उपलब्ध डेटा, उदाहरणतः पूर्णकालिक शिक्षा में बच्चों की प्रतिशतता या भिन्न देशों में स्तनपान की विशेष दरें) दे सकते हैं, और उनसे उन प्रश्नों के बारे में सोचने के लिए कह सकते हैं जो आप इस डेटा के बारे में पूछ सकते हैं
- विद्यार्थियों के सप्ताह भर के प्रश्नों को सूचीबद्ध करते हुए प्रश्न दीवार डिज़ाइन कर सकते हैं।
जब विद्यार्थी प्रश्न पूछने और उन्हें मिलने वाले प्रश्नों के उत्तर देने के लिए मुक्त होते हैं तो उस समय आपको रुचि और विचारशीलता के स्तर को देखकर हैरानी होगी। जब विद्यार्थी अधिक स्पष्टता और सटीकता से संवाद करना सीख जाते हैं, तो वे न केवल अपनी मौखिक और लिखित शब्दावलियां बढ़ाते हैं, अपितु उनमें नया ज्ञान और कौशल भी विकसित होता है।
अतिरिक्त संसाधन
- ‘Proof – sum of measures of angles in a triangle are 180’ by Khan Academy: https://www.khanacademy.org/ math/ geometry/ angles/ v/ proof---sum-of-measures-of-angles-in-a-triangle-are-180
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- Class X maths study material: http://www.zietmysore.org/ stud_mats/ X/ maths.pdf
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- OpenLearn: http://www.open.edu/ openlearn/
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Mathcelebration: http://www.mathcelebration.com/
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Maths is Fun: http://www.mathsisfun.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Central Board of Secondary Education’s books and support material (also including the Teachers Manual for Formative Assessment – Mathematics (Class IX)) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
अभिस्वीकृतियाँ
तृतीय पक्षों की सामग्रियों और अन्यथा कथित को छोड़कर, यह सामग्री क्रिएटिव कॉमन्स एट्रिब्यूशन–शेयरएलाइक लाइसेंस के अंतर्गत उपलब्ध कराई गई है (http://creativecommons.org/ licenses/ by-sa/ 3.0/)। नीचे दी गई सामग्री मालिकाना हक की है तथा लाइसेंस के अंतर्गत ही इस प्रोजेक्ट में उपयोग की गई है, तथा इसका Creative Commons Licence से कोई वास्ता नहीं है। इसका अर्थ यह है कि यह सामग्री अपरिवर्तित रूप से केवल TESS-India प्रोजेक्ट में ही उपयोग की जा सकती है और यह किसी अनुवर्ती OER संस्करणों में उपयोग नहीं की जा सकती। इसमें TESS-India, OU और UKAID लोगो का उपयोग भी शामिल है। इस यूनिट में सामग्री को पुनः प्रस्तुत करने की अनुमति के लिए निम्न स्रोतों का कृतज्ञतारूपी आभार किया जाता हैः
चित्र 1: द ओपन यूनिवर्सिटी के लिए क्लेयर ली (Figure 1: Clare Lee for The Open University).
कॉपीराइट के स्वामियों से संपर्क करने का हर प्रयास किया गया है। यदि किसी को अनजाने में अनदेखा कर दिया गया है, तो पहला अवसर मिलते ही प्रकाशकों को आवश्यक व्यवस्थाएं करने में हर्ष होगा।
वीडियो (वीडियो स्टिल्स सहित): भारत भर के उन अध्यापक शिक्षकों, मुख्याध्यापकों, अध्यापकों और विद्यार्थियों के प्रति आभार प्रकट किया जाता है जिन्होंने उत्पादनों में दि ओपन यूनिवर्सिटी के साथ काम किया है।
