Resource 4: Translating and reflecting triangles

 Background information / subject knowledge for teacher

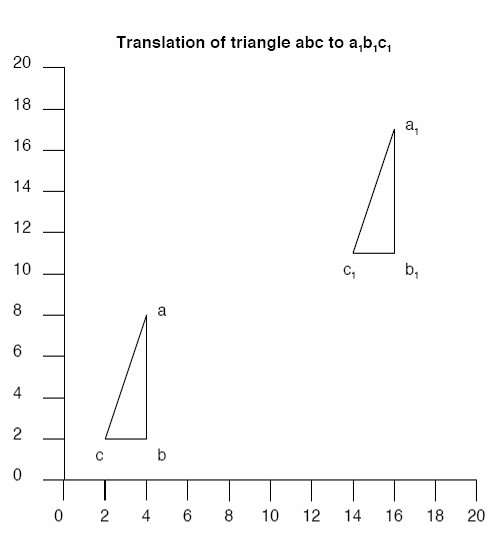
x-y coordinates always give the ‘x’ (horizontal axis) value before the ‘y’ (vertical axis) value.

So, in the illustration, the x-y coordinates for abc:

  • a = 4, 8
  • b = 4, 2
  • c = 2, 2

The translation to a1b1c1 increases the value of x by 12, and y by 9. So:

  • a1 = 16, 17
  • b1 = 16, 11
  • c1 = 14, 11

Differentiation

This can be made simple, by moving a cut-out shape around the grid, drawing around it and recording the new coordinates.

This can be made more challenging by giving coordinates for a shape and asking pupils to draw the shape. Then say how a translation affects the x-y values, and ask them to work out the new coordinates and redraw the position of the shape.

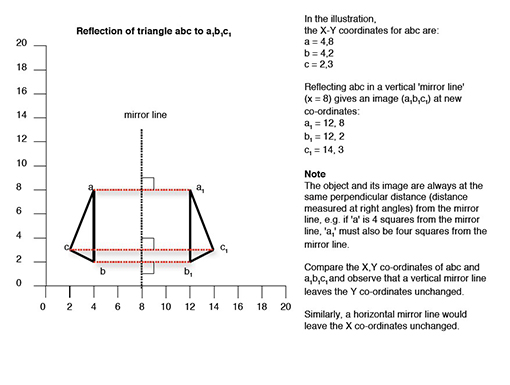
In the illustration, the x-y coordinates for abc are:

  • a = 4, 8
  • b = 4, 2
  • c = 2, 3

Reflecting abc in a vertical ‘mirror line’ (x=8) gives an image (a1b1c1) at new coordinates:

  • a1 = 12, 8
  • b1 = 12, 2
  • c1 = 14, 3

Note

The object and its image are always at the same perpendicular distance (distance measured at right angles) form the mirror line, e.g. if ‘a’ is 4 squares from the mirror line, ‘a1’ must also be 4 squares from the mirror line.

Compare the x-y coordinates of abc and a1b1c1 and observe that a vertical mirror line leaves the y coordinates unchanged.

Similarly, a horizontal mirror line would leave the x coordinates unchanged.

Original Source: http://www.bbc.co.uk/ schools [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] (Accessed 2008)

Resource 3: Translation

Acknowledgements