Resource 4: Translating and reflecting triangles

 Teacher resource for planning or adapting to use with pupils

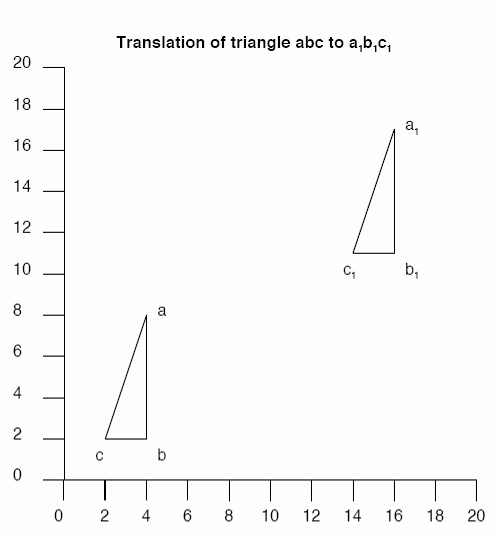
X-Y coordinates always give the ‘x’ (horizontal axis) value before the ‘y’ (vertical axis) value.

So, in the illustration, the X-Y coordinates for abc:

  • a = 4, 8
  • b = 4, 2
  • c = 2, 2

The translation to a1b1c1 increases the value of x by 12, and y by 9. So:

  • a1 = 16, 17
  • b1 = 16, 11
  • c1 = 14, 11

Differentiation

This can be made simple, by moving a cut-out shape around the grid, drawing around it and recording the new coordinates.

This can be made more challenging by giving coordinates for a shape and asking pupils to draw the shape. Then say how a translation affects the X-Y values, and ask them to work out the new coordinates and re-draw the position of the shape.

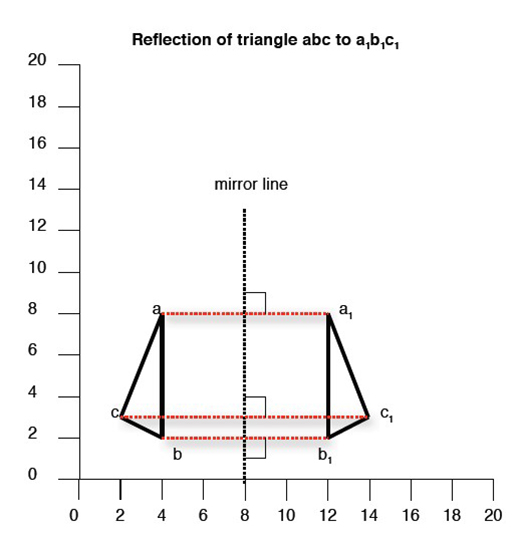
In the illustration, the X-Y coordinates for abc are:

  • a = 4, 8
  • b = 4, 2
  • c = 2, 3

Reflecting abc in a vertical ‘mirror line’ (x=8) gives an image (a1b1c1) at new coordinates:

  • a1 = 12, 8
  • b1 = 4, 2
  • c1 = 4, 3

Note

The object and its image are always at the same perpendicular distance (distance measured at right angles) form the mirror line, e.g. if ‘a’ is 4 squares from the mirror line, ‘a1’ must also be 4 squares from the mirror line.

Compare the X-Y coordinates of abc and a1b1c1 and observe that a vertical mirror line leaves the Y coordinates unchanged.

Similarly, a horizontal mirror line would leave the X coordinates unchanged.

Adapted from: BBC Schools, Website

Resource 3: Translation