Appendix 2: Teacher notes - outputs of the lesson (Exploring the properties of electrons using a fine beam tube)

Appendix 2: Teacher notes - outputs of the lesson

The fine beam tube is a challenging experiment that draws on a number of different concepts delivered in SHS Physics Year 2. It would be worth using it only after teaching all of the material listed below. Alternatively, it could be delivered in Year 3 as a vehicle for revising these concepts.

Section

Unit

Objectives

Content

2 Mechanics

1 Energy

2.1.1, 2.1.2

Energy and conservation of energy

 

2 Circular motion

2.2.2

Centripetal force

5 Electricity and magnetism

2 Magnets

5.2.2

Magnetic field

 

3 Electro-magnetism

5.3.1

Magnetic fields created by current

 

 

5.3.2

Fleming’s Left- Hand Rule

 

 

5.3.6

Force on a charged particle in a magnetic field and Electric field

6 Atomic and nuclear physics

2 Thermionic Emission

6.2.1, 2

Thermionic emission and cathode rays

Comments on Background

The fine beam tube (FBT) is an application that uses thermionic emission to produce an electron beam (Unit 2 Objectives 6.2.1, 2). The electric field forces in the anode accelerate the electrons and their speed can be calculated by conservation of energy (Unit 1, 2.1.1,2) such that the electrical work done accelerating the electrons = gain in kinetic energy.

The two coils produce a magnetic field between them (Unit 3, 5.2.2, 5.3.1). The field produces a force on the electrons, the direction is given by Fleming’s Left Hand Rule (Unit 3, 5.3.2) and the magnitude of the force using the formula given in Unit 3, section 5.3.6. Since the direction of the force is perpendicular to the velocity of the electrons, the force provides a centripetal acceleration (Unit 2, section 2.2.2) making the electrons travel in a circle.

However, the Helmholtz configuration is not introduced in SHS Physics, so this is an extension exercise, which serves as a synoptic task. By combining the equations given in these sections with additional equations for the specific magnetic field here, it is possible to derive a framework to investigate the relationship between

  • The voltage used to accelerate the electrons (linked to their speed), V
  • The current in the coils (which causes the magnetic force), I
  • The radius of the electron beam, r

The exemplar shows how one relationship can be investigated graphically. At a higher level, the data can be used to determine the charge to mass ratio of an electron e divided by m sub e , using a single set of data or the gradient of a graph


Comments on Practical Activity

This section starts with a detailed account of the apparatus and its parts. The experiment is an Interactive Screen Experiment which is based on many photographs of a real set of apparatus showing all possible combinations of current, voltage, polarity and the resulting beam. Changing a slider changes the image smoothly to a different image with a different set of parameters so is close to running the experiment for real.


Comments on Investigating the Beam

This is a series of three short tasks to qualitatively investigate the behaviour of the beam, changing the voltage, current and polarity. For some student groups, it may only be sufficient to explore this task.


Comments on Making Measurements with a circular beam in the FBT

This is the quantitative investigation. It explains the data collection, graph plotting and calculation of e divided by m sub e

Using just data and graphically. These tasks build in difficulty so that the teacher can decide which tasks are appropriate to their students.

The algebra may be on the limit of what students are prepared for and has been simplified as much as possible to calculate e divided by m sub e Students will need access to a scientific calculator (e.g., one on a computer) as they will manipulate small numbers written in scientific notation and plot small numbers on the graph.


Mathematical background

Symbols used:

V = accelerating voltage

q = charge on a particle

e = charge on an electron = 1.602 × 10-19 C

m = mass of a particle

me = electron mass = 9.109 × 10-31 kg

v = velocity of an electron

B = magnetic field

F = force

r = radius of circular beam

theta  = angle between magnetic field and velocity, 90° in this context

ratio = e/me = 1.76 × 1011 C kg-1

N  = number of turns of wire in each of the coils = 130 here

R = radius of each coil = 15 cm here

μ0 = permeability of free space = 4 π × 10-7 T m A-1

k = coils constant = 7.793 multiplication 10 super negative four  T m-1 for these coils

Work done on electron = gain in kinetic energy.

Work done accelerating through cap v equals q times cap v comma q equals e  and mass  equals m sub e

The magnetic field force cap f equals cap b times q times v times sine of theta  where q equals e  and  theta equals 90 degree

The magnetic field provides the centripetal force,  cap f equals m times v squared divided by r

cap b times e times v equals m sub e times v squared divided by r times left parenthesis two right parenthesis

From (2)

cap b times e times r equals m sub e times v

v equals cap b times e times r divided by m sub e

v squared equals left parenthesis cap b times e times r divided by m sub e right parenthesis squared

Using (1)

e times cap v equals one divided by two times m sub e times left parenthesis cap b times e times r divided by m sub e right parenthesis squared

cap v equals one divided by two times cap b squared times r squared of e divided by m sub e

In the language used here, where  r times a times t times i times o equals e divided by m sub e

cap v equals one divided by two times cap b squared times r squared times r times a times t times i times o  (3)

The last step is the relationship between B and I. The theory here is well beyond the level of SHS, so here is the given formula.

cap b equals left parenthesis four divided by five right parenthesis super three divided by two times mu sub zero times cap n times cap i divided by cap r

This is simplified to cap b equals k times cap i  where

k equals left parenthesis four divided by five right parenthesis super three divided by two times mu sub zero times cap n divided by cap r

For this coil, R  = 15.0 cm = 0.0150 m and N = 130 terms. Hence the coils constant k = 7.793 multiplication 10 super negative four  T m-1 for this apparatus

The final formula that links the experiment

cap v equals one divided by two times k squared times cap i squared times r squared times r times a times t times i times o

This can be used as the basis of any investigation where you might want to fix one of (V, I, r) and vary/measure the other two.

Sample dataset

The experiment has three variables – V, I and r. It is possible to choose a constant value of one and investigate the relationship of the other two. Here, the instructions investigate the relationship between V and r (V∝ r2) with a fixed current as it is the easiest process to explain. It is possible to do two more investigations fixing r or V. The data can be manipulated into a straight-line graph for either of these combinations and the gradient used to determine . This could also be a planning exercise for some students.

Current I = 1.52 A

Voltage / V

Left position /cm

Right position / cm

Diameter / cm

Radius / m

Radius2 / m2

130

10.3

16.0

5.7

0.0285

0.00081

150

10.3

16.5

6.2

0.0310

0.00096

170

10.3

17.0

6.7

0.0335

0.00112

190

10.3

17.3

7.0

0.0350

0.00123

210

10.3

17.7

7.4

0.0370

0.00137

230

10.3

18.0

7.7

0.0385

0.00148

250

10.3

18.3

8.0

0.0400

0.00160


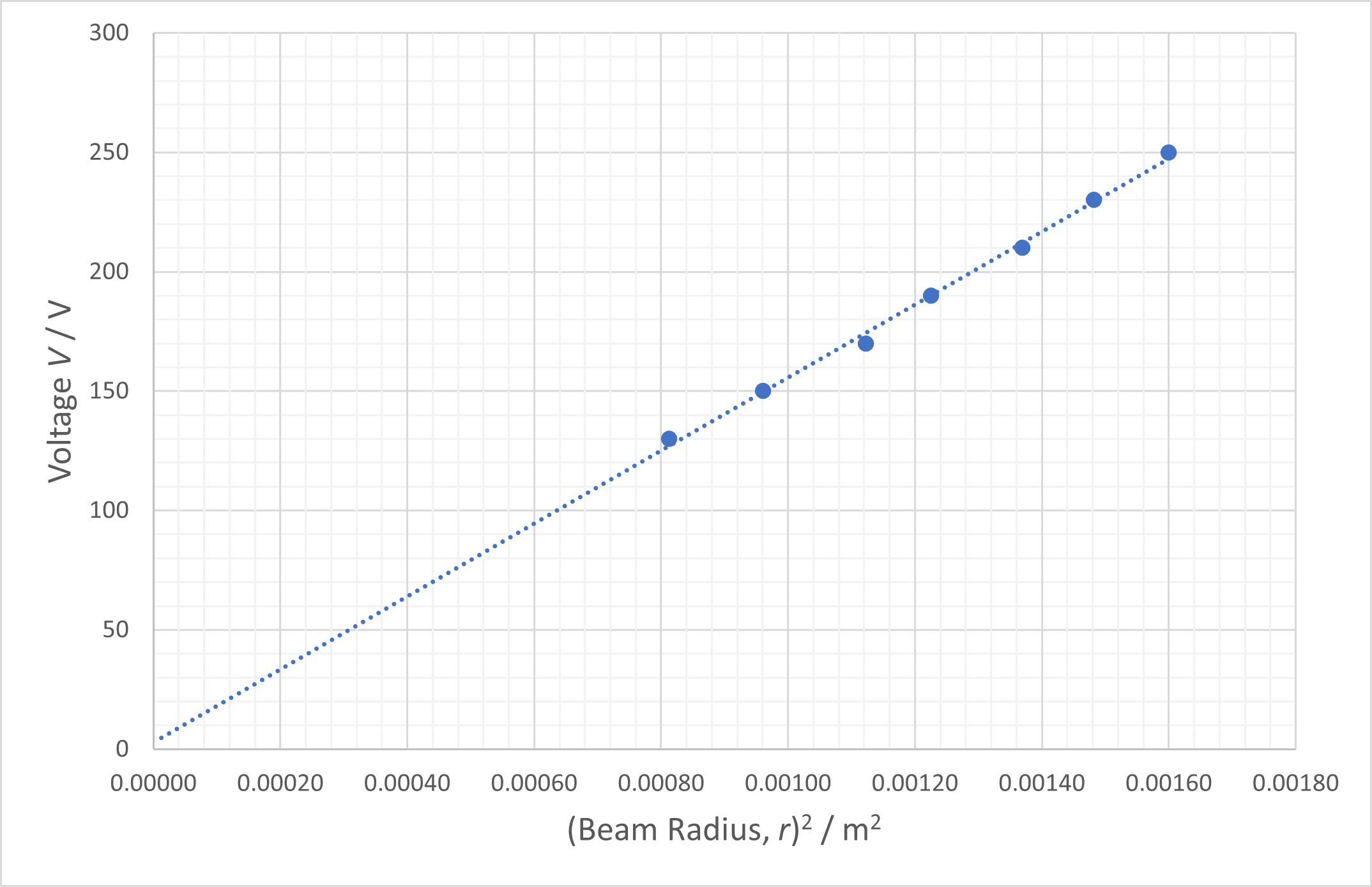
Graph showing Voltage against (Beam Radius)2 for the Fine Beam Tube, current fixed at 1.52 A

The gradient is 1.53 × 105 V m-2

Sample single calculation of  bold-italic e divided by bold-italic m sub bold-italic e

Using the last row of the table and the answer to ITQ 6

cap b equals k times cap i

equals 7.793 multiplication 10 super negative four times cap t times m super negative one multiplication 1.52 times cap a

equals 0.0011845 times cap t


r times a times t times i times o equals two times cap v divided by cap b squared times r squared

equals two multiplication 250 times cap v divided by left parenthesis 0.0011845 times cap t postfix multiplication full stop 0400 times m right parenthesis squared

equals 2.23 multiplication 10 super 11 times cap c times k times g super negative one

Sample calculation bold-italic e divided by bold-italic m sub bold-italic e  from graph

Using the answer to ITQ 7, B calculated above and the gradient of the graph

r times a times t times i times o equals two multiplication 1.53 multiplication 10 super five times cap v times m super negative two divided by left parenthesis 0.0011845 times cap t right parenthesis squared

equals 2.18 multiplication 10 super 11 times cap c times k times g super negative one

Final value of bold-italic e divided by bold-italic m sub bold-italic e  and uncertainties

The calculated value of e solidus m sub e  in this experiment is consistently higher than the established value of 1.76 × 1011 C kg-1. With care, it is possible to get a graph showing a good straight line of best fit, through the origin, with little scatter around the line. There is plenty of scope for considering the uncertainties in the measurements of beam radius, voltage and current. There is scope to instruct students to repeat measurements of the radius.

The diameter of the coil and number of turns in each coil uses values provided by the manufacturer. They in turn are used in the calculation of  k used to determine the value of the magnetic field. That assumes that the separation of the 2 coils and alignment is as close as possible to the ideal Helmholtz configuration.


Extension questions

Below are some extension questions you may wish to use with your more advanced students.

Question A

Why does an increase in the coil current lead to a smaller radius for the electron beam?

Answer for Question A

The magnetic field is proportional to this current so it increases. The force provides a stronger centripetal force, cap f sub c times e times n times t times r times i times p times e times t times a times l equals m times v squared divided by r which in turn is inversely proportional to the radius of the path. So, a stronger field supports a smaller circle for constant velocity.


Question B

Why would you not be able to perform this experiment with a vacuum in the vacuum tube?

Answer for Question B

You would not be able to see the electron beam. The faint lilac glow of the beam arises from collisions between the electrons and hydrogen atoms. The electron within the atom is excited to a higher energy level


Question C

Why did we ask you to do experiments with quite small circles, radius up to about 4 cm?

Answer for Question C

The Helhmoltz configuration of two coils is about as good as a physicist can do to produce a uniform magnetic field. It is extremely close to uniform for a cylindrical region between these coils up to a radius up to about 4 cm from the axial line through the centre of the 2 coils. Thereafter, it decreases significantly. This experiment is constrained by having the beam within the region which shows the most uniformity. So, we asked you to use a current of about 1.5 A to limit this

You could use a bigger current and smaller circles, but that may not give the best results. The beam can only be measured with limited precision (e.g. random uncertainty of ± 1 – 2 mm, so a smaller radius would have a larger percentage of fractional uncertainty).


More challenging questions

Question D

Calculate the velocity of the electron using your value of bold-italic e divided by bold-italic m sub bold-italic e when the accelerating voltage = 220 V.

Hint – the electrical energy given to the electron is its charge × voltage and this is converted into kinetic energy cap k times cap e equals one divided by two times m times v squared

Answer for Question D

Using e times cap v equals one divided by two times m times v squared

Rearrange for v comma v equals Square root of two times e divided by m sub e times cap v

Example, with cap v equals 220 cap v and e divided by m sub e equals 1.8 multiplication 10 super 11 cap c k g super minus one

v equals Square root of two multiplication 1.8 multiplication 10 super 11 cap c k g super minus one multiplication 220 cap v

v equals 8.9 multiplication 10 super six m s super minus one

So, the voltage accelerates the electron to almost 10 million m s-1.


Question E

Calculate e divided by m sub e with the following data – cap v = 220 V, cap i =1.60 A, r sub b times e times a times m = 0.040 m

Answer for Question E

Using

cap v equals one divided by two times cap b squared times r squared times r times a times t times i times o of one

First work out B

cap b equals k times cap i

equals 7.793 multiplication 10 super negative four times cap t times m super negative one multiplication 1.60 times cap a

equals 0.0012467 times cap t

Rearranging (1) and using the value for B

r times a times t times i times o equals two times cap v divided by cap b squared times r squared

equals two multiplication 220 times cap v divided by left parenthesis 0.0012467 times cap t right parenthesis squared multiplication left parenthesis 0.040 times m right parenthesis squared

e divided by m sub e equals 1.8 multiplication 10 super 11 cap c k g super minus one



Previous: Appendix 1     Next: Lesson: Investigating the properties of electrons using a fine beam tube