Practical activity

In lesson 1 Determining a spring force constant you discovered that the spring force constant of a spring can be calculated by measuring the extension of the spring after the addition of a weight and then applying Hooke’s law. In this activity you will use the ‘Simple harmonic oscillation’ option located in the Spring mass system application to examine the dynamic properties of an oscillating spring and use your observations to calculate the spring force constant using the period of oscillation and the weight (mass) added to the spring. However, your first task is to examine the relationship between the weight added to a spring, the displacement (amplitude) used to initiate the oscillation and the period of the oscillation.

Before you access the Spring mass system application homepage, first read the following instructions.

Task 1

Your first task is to explore the relationship between the weight (mass) added to a spring, the displacement applied to a weighted spring (the amplitude) to initiate harmonic oscillation, and the period of oscillation.

Copy the following table headings into your laboratory notebook. You will use this to record the data generated by the spring mass system.

Figure 5 The table headings used for the investigation of simple harmonic oscillations using the spring mass system application.

When you access the experimental homepage (do not do this until you have read the instructions thoroughly), select the ‘Simple harmonic oscillation’ option and enter the experiment. 

You will have the choice of two springs (a soft and a stiff spring). Once you have selected a spring, use the sliding bar to select and add a weight to the spring and then wait for the spring to settle at its new equilibrium point. 

Once the spring has settled, use the cursor (together with the left click function on a PC mouse) to drag the weight downwards, extending the spring and then release the weight (by releasing the left click button). The weighted spring will now oscillate until it comes to rest at its equilibrium point. You have three options for measuring the period of oscillation. The one that closely resembles a laboratory is the ‘Unlimited’ option. If selected, the spring will oscillate until it comes to a stop, and you will need to use a stopwatch to calculate the period. The other two options will stop the spring oscillating after 10 and 20 cycles respectively. For the purposes of Task 1, select the ‘10’ oscillations option. Remember to divide the time recorded by the number of oscillations to obtain the period (the time it takes to complete a full cycle).

Now you are ready to collect your data. For your chosen weight and spring, apply a series of different displacements (amplitudes) and record your observations. 

Look at your recorded observations and discuss the relationship between mass, amplitude and period with your classmates.

Task 2

In this task you will use the mass and period to calculate the spring force constant of your chosen spring. For this experiment, select a spring and then starting with the 25 g weight, apply a series of amplitudes and record your settings and the periods in your laboratory notebook. Now repeat this process using the 50 g weight and then the 100 g weight.

Remember, if you use the ‘10’ or ‘20’ oscillations option, you will need to divide the recorded time by the number of oscillations to obtain the period.

The following equation can be used to calculate the period if the mass and spring force constant are known:

Here, the period (T) is measured in seconds (s), the mass (m) in kilograms (kg) and the force constant (k) in newtons per metre (N/m).

This equation can be arranged so that the force constant can be measured using the slope of a graph.

This is achieved by first squaring the period (so T becomes T²).

And then rearranging the equation further so mass (m) becomes a separate quantity.

Now a plot of T² against mass will have a slope that approximates the quantity

And can be rewritten so slope = , and from this a simple rearrangement will give the equation for the force constant (k).

k = 4π²/slope

Using your observation, plot the square of the period (s²) against the mass (kg) and use the slope to calculate the spring force constant (Figure 6).

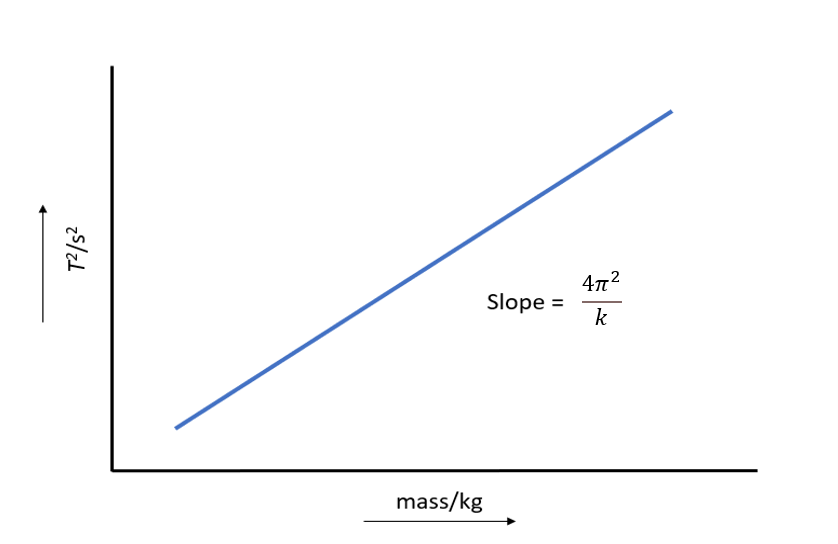
Figure 6 The spring force constant can be calculated using the slope of the square of the period against mass.

Now that you have read these instructions you are ready to enter the experiment.

Spring mass system

Click on the icon below to access the Spring mass system application homepage in the OpenSTEM Africa Virtual Laboratory. Watch the introductory video before entering the experiment.

Previous: Background                                                                                   Next: Summary