 Al Capone's police mugshot
Al Capone's police mugshot
Al Capone’s criminal organization existed before the days of Facebook, Twitter, and CompStat, but the continuation and prominence of his syndicate relied on the power of social networks. To analyze the role of social networks in organized crime, we took network science — a cutting edge computational approach that maps and measures relationships between people — and applied it to Prohibition Era Chicago. Nearly a century ago, the US prohibited the production and distribution of alcohol under the 18th Amendment. This social experiment, known as Prohibition, lasted only 14 years, but had the long-term consequence of strengthening organized crime throughout the US especially in cities like Chicago. Our recent study shows how multiple types of relationships formed and sustained Al Capone’s criminal network.
Capone and his cronies did not leave a digital breadcrumb trail of data on their social relationships; indeed, the nature of organized crime demanded secrecy—well before an organization like WikiLeaks existed. Fortunately for our purposes, a public fascination with Capone’s wealth, moxie, and violence dating back to the 1920s meant that thousands of pages of documents related to Capone’s organized crime were preserved in Chicago archives. We combined big data thinking with old school gumshoe-like archival work with Al Capone as our informant. We accessed more than 5,000 pages of historical documents such as investigator notes, legal documents, letters, and newspaper clippings from archives including the Chicago Crime Commission, the National Archives, the FBI, and the IRS. Dusty boxes and crumbling pages contained nuggets of information on Al Capone, his friends, and the friends of his friends.
We organized information on each event, individual, and relationship into a relational database, and our analysis revealed 1,030 people whose criminal activities directly or indirectly connected them to Al Capone. However, the organized crime network also contained personal relationships, such as family members and friendships, and legitimate relationships that were completely legal but easily corruptible, such as co-owning businesses, political associations, or union associations. Success in organized crime required knowing when and where raids would occur, ensuring that the top guys of the syndicate were not present during those raids, knowing which agents would take a bribe, and guaranteeing that prosecutors never had enough evidence to convict. Financial success in organized crime permitted new investments ranging from small businesses, such as dog racetracks and dry cleaning shops, to political campaign donations, and these investments opened up new legitimate spheres to organized crime individuals.
The network property of multiplexity is essential to understanding relationships in organized crime. Multiplexity occurs when more than one type of relationship exists between two people. For example, work colleagues who are also friends have multiplex relationships because they have at least two distinct types of relationships between them. Multiplexity is a powerful feature of networks because it adds depth to social relationships while also incurring a higher cost of relationship failure. In the multiplex example of co-workers who are also friends, work may suffer if the friends get into a disagreement.
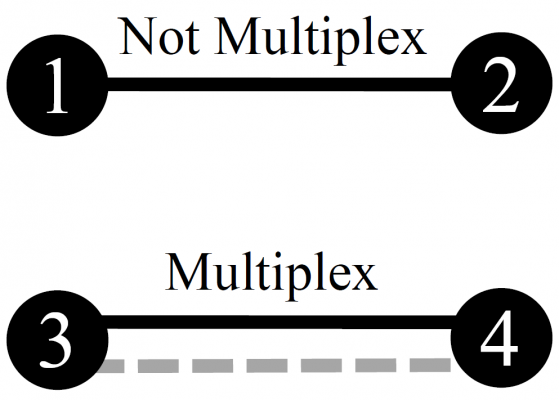 Figure 1: Non-multiplex and multiplex relationships between pairs
Figure 1: Non-multiplex and multiplex relationships between pairs
Multiplexity was a rare but incredibly relevant property of Chicago’s Prohibition era network. Our study finds that only 10 percent of the relationships between organized crime individuals contained more than just criminal activity but that these overlapping multiplex relationships were essential to the operation of organized crime. Figure 2 shows the same group of 1,030 organized crime individuals and each configuration plots the three very different types of relationships between them. The lower right panel plots only the 10 percent of relationships across all three networks that were multiplex—each line symbolizing at least two of the three types of possible relationships.
 Figure 2: Criminal, personal, legitimate, and multiplex networks in early 1900s Chicago organized crime. Note: Figure originally printed in Smith and Papachristos (2016). Individuals with zero relationships in each network are light gray; individuals that had relationships in each network are black.
Figure 2: Criminal, personal, legitimate, and multiplex networks in early 1900s Chicago organized crime. Note: Figure originally printed in Smith and Papachristos (2016). Individuals with zero relationships in each network are light gray; individuals that had relationships in each network are black.
Even though multiplexity was rare in organized crime, overlapping criminal, personal, and legitimate relationships demonstrated that people had to trust each other during risky situations and shady dealings, even when corruption and violence were tools of the trade. When groups of ordinary bootleggers, brothel owners, and bookies organized and infiltrated police departments, courtrooms, unions, and political offices through overlapping relationships, organized crime developed and integrated into mainstream society. In fact, we argue that the intersection of criminal, legitimate and personal networks was where organized crime took place in Chicago. We conclude that even though multiplexity was not pervasive in organized crime, multiplexity glued the underworld and upper worlds together above and beyond the personalities of famous gangsters like Al Capone and general associations between ethnic groups. When networks and actions teeter into uncertain, unregulated, or risky domains, trusting your crooked neighbors may very well be critical—even if you trust only a few of them.
Our findings have implications for the study of organized crime and the study of social networks more broadly. With regard to organized crime, our results highlight the ways multiplexity links the underworld and the upper world — a process that organizes crime into mainstream society and, specifically, institutionalized Prohibition networks within the city of Chicago. The rarity of multiplexity highlights the difficulty of locating trustworthy bridges when one cannot trust just any crook, neighbor, or politician, even when multiplexity brought the spheres of organized crime together.
This article is based on the paper Trust Thy Crooked Neighbor: Multiplexity in Chicago Organized Crime Networks in American Sociological Review and was originally published under a CC-BY-NC licence by the LSE USAPP Blog

Rate and Review
Rate this article
Review this article
Log into OpenLearn to leave reviews and join in the conversation.
Article reviews