4.6  Average densities

If a planet is composed of different layers each having different densities, then the density of the planet as a whole will be averaged over the various layers. To give the average density of a planet, the total mass is divided by the total volume:

In this way you can measure the average densities of some planets orbiting around other stars even though you can’t see them, as you will learn in future weeks. If a planet has the density of rock, it is probably composed of rock. If it has the density of hydrogen gas, that is probably what it is composed of. Iron is the densest material you might expect to find in a planet, while a mixture of hydrogen gas with a small amount of helium is the least dense material you might expect to find.

However, you must be careful about conclusions such as those above. The average density of a planet might not tell you what the planet is made of. It is possible to imagine a planet with an iron core surrounded by hydrogen/helium gas, which averages out to exactly the density of rock. In this case, the conclusion that the planet is composed of rock would be completely wrong. From the average density, it is impossible to be sure exactly how much of each layer is present.

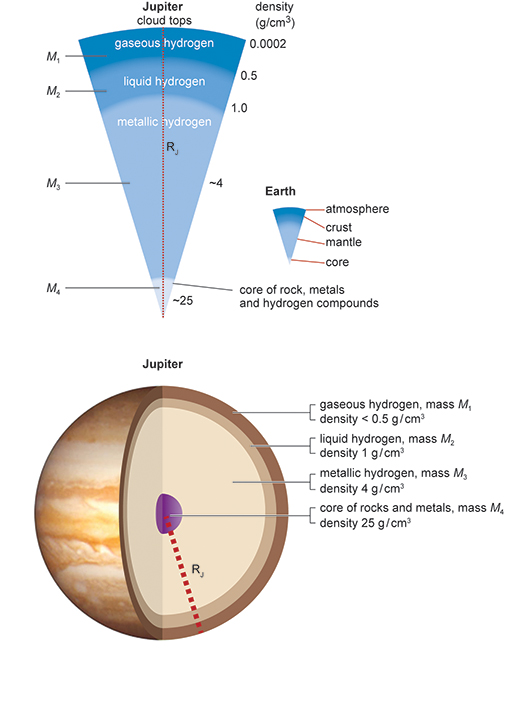
As you go down to deeper layers of the planet Jupiter, you can see how much the density increases (Figure 12). Density is often expressed in units of grams per cubic centimetre (g/cm³), so the numbers in Figure 12 say how many grams of material are contained in each cubic centimetre. Near the core the density is expected to be around 25 g/cm³, which means that each centimetre cube contains material that has a mass of 25 grams. As a comparison, the density of liquid water on Earth is 1 g/cm³.

Figure 12  Density of Jupiter’s layers

Show description|Hide description

This is a diagram demonstrating the density of Jupiter’s layers. There is a segment in the shape of an upside down triangle at the top of the image, with different shades of blue, the darkest being at the top and the lightest shade at the bottom. There are four different shades, labelled on the left-hand side from the bottom: M₄, M₃, M₂, M₁. There is a red dashed line running down the middle, from top to bottom, labelled R_J. On the right-hand side, there is the label at the top: density (g/cm³), with the following numbers at each different shade, from the bottom to the top: ~25, ~4, 1.0, 0.5 and the top right edge of the section has 0.0002. Below this, there is a diagram of Jupiter, with a segment cut away displaying the core. There is a dashed line coming from the core to the edge, labelled R_J. From the outer edge to the core there are four labels: gaseous hydrogen, mass M₁ density <0.5 g/cm³; liquid hydrogen, mass M₂ density 1 g/cm³; metallic hydrogen, mass M₃ density 4 g/cm³; core of rocks and metals, mass M₄ density 25 g/cm³.

Figure 12  Density of Jupiter’s layers

Maths help

The following OpenLearn resources may help with the maths in this section. Open the link in a new tab or window by holding down Ctrl (or Cmd on a Mac) when you click on the link. Remember to return here when you have finished.

• using formulas (Sections 3.1, 3.1.1, 3.2, 3.3 and 3.3.1) [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)]
• scientific notation on your calculator (Sections 5 and 5.1)
• rounding (nearest 10, 100, 1000) (Section 2)
• rounding (decimal places and significant figures) (Sections 1.4, 1.4.1, 1.5 and 1.5.1)
• how precise are the measurements? (Section 4)