The equation for the area of a circle

The area of a circle is related to the radius of the circle, just as the volume of a sphere is related to the radius of the sphere as you saw in Week 2. Remember that the radius of the two-dimensional circle we see as a star is actually the same as the radius of the three-dimensional, spherical star itself.

It has been known since at least the time of the ancient Babylonians that the area of a circle is a little more than three times its radius squared. To find the exact area of a circle the radius squared is multiplied by a numerical constant called ‘pi’, which has the symbol π and is pronounced ‘pie’. Pi is close to the value 3.14, but if you have a calculator with a ‘π’ button it’s best to use that when working out areas and volumes.

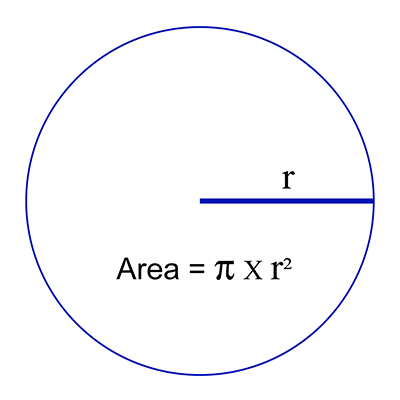
So, the area of a circle is given by:

which can also be written as:

This is shown in Figure 13.

Figure 13  Area of a circle with radius r

For example, the area of a circle with a radius of 10 m would be

Generally, you measure area in m² or cm².

The cross-sectional area of a sphere with radius 10 m would also be 314 m².