4.4 Spectra, the Doppler effect and radial velocities
When stars wobble and their light is Doppler stretched or compressed, the colour and therefore the wavelength of the light you see changes slightly. This means that the wavelengths of those tell-tale fingerprints – the absorption lines – in the star’s spectrum will also vary. Because you know precisely which wavelengths those fingerprints should occur at, you can measure how much they have changed to work out how fast, and in what direction, the star is moving.
Video 1 shows how a star wobbles as a planet orbits it, and how absorption lines in the star’s spectrum shift with the tiny wavelength changes. This method of detecting exoplanets is called the ‘radial velocity’ method – you’ll learn why we use this term in a moment.
Activity _unit4.4.1 Activity 3 How is the star moving?
a.
towards you, slowly
b.
away from you, fast
c.
not moving away from you or towards you
d.
away from you, slowly
The correct answer is a.
Answer
The light from the star has got bluer – we can see this because the absorption lines have shifted towards the blue end of the star spectrum. Blue light has a shorter wavelength so this means that the light waves have been compressed. So, we can tell that the star was moving towards us.
The absorption lines have only shifted by a very small amount so the star must be moving relatively slowly towards us.
a.
towards you, slowly
b.
away from you, fast
c.
not moving away from you or towards you
d.
away from you, slowly
The correct answer is b.
Answer
The light from the star has got redder – we can see this because the absorption lines have shifted towards the red end of the star spectrum. Red light has a longer wavelength so this means that the light waves have been stretched out. So, we can tell that the star was moving away from us.
The absorption lines have shifted by a greater amount than in Figure 8 so the star must be moving relatively fast away from us.
a.
towards you, slowly
b.
away from you, fast
c.
not moving away from you or towards you
d.
away from you, slowly
The correct answer is c.
Answer
The light from the star hasn’t changed colour – we can see this because the absorption lines are in the same place as the laboratory spectrum. So, we can tell that the star wasn’t moving towards or away from us. (It could still be moving across our line of sight however.)
a.
towards you, slowly
b.
away from you, fast
c.
not moving away from you or towards you
d.
away from you, slowly
The correct answer is d.
Answer
The light from the star has got redder – we can see this because the absorption lines have shifted towards the red end of the star spectrum. Red light has a longer wavelength so this means that the light waves have been stretched out. So, we can tell that the star was moving away from us.
The absorption lines have only shifted by a very small amount so the star must be moving relatively slowly away from us.
The compression, or stretching, of waves tells you about motion towards or away from you. Imagine yourself at the centre of an enormous sphere. If something moves outwards from you at the centre, in whatever direction, its light will be stretched. If it moves inwards towards you, its light will be compressed. The Doppler shift therefore tells you about motion in a particular direction along the radius of the imaginary sphere. For this reason, the velocity you can work out from the wavelength shift is called the radial velocity.
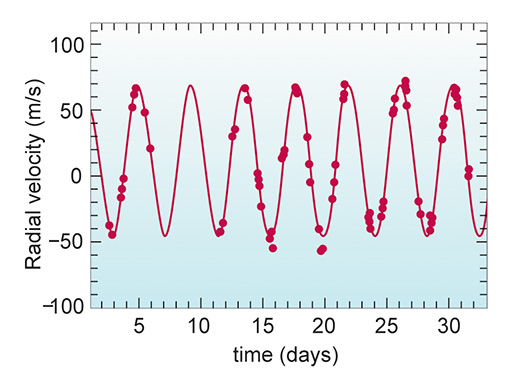
During a planet’s orbit, its star’s speed is constant. But, because the direction of the star’s motion changes continually, the velocity also changes continually. As the velocity changes, the star’s motion towards and away from you also changes. Or in other words the star’s radial velocity changes. Sometimes the star is not moving towards or away from you at all, sometimes it is moving towards you, and sometimes it is moving away from you. These changes in radial velocity cause changes in the measured wavelengths of the chemical fingerprints – the patterns of absorption lines. You can translate the wavelength changes into the speed of motion towards or away from you, and these changes can be shown on a graph. This graph is called a radial velocity curve. Here’s the curve for the star 51 Pegasi (Figure 12).
Here you can see the measurements of 51 Pegasi’s radial velocity that enabled the planet 51 Pegasi b to be detected. You can see the (horizontal) space between peaks is around four days, which is how long it takes 51 Pegasi b to orbit its star. The star moves relative to us at a maximum speed of about 50 metres per second (m/s).
ITQ _unit4.4.1
-
Planetary systems can be oriented in any random way relative to our line of sight. In Section 3.5, as shown in Figure 13, your viewpoint on the orbiting star and planet was looking down from above. Describe the radial velocity graph for a planetary system oriented like this.
-
From this viewpoint, neither the star nor the planet move towards or away from you. As radial velocity is the motion towards or away from you, it is exactly zero at all points around the orbit. The graph would therefore be a straight line with radial velocity equal to zero throughout the orbit.