3.1 Using fractions and percentages
One way of better understanding the impact of the Browns’ water savings is to express them as fractions and percentages.
Using the example of the Browns’ first water saving measure, not using water outside the house, we can calculate that as a fraction. A fraction should be expressed as a numerator (the saving) and a denominator (the total water used):
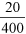
In this case the units cancel each other out:
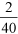
Fractions can be simplified when the numerator and denominator have a common factor in them. If both the numerator and denominator have common factors, then we can cancel these factors out. In this case the common factor is 2. It is therefore possible to simplify the fraction by cancelling the 2 from both the numerator and denominator of the fraction. Cancelling is equivalent to dividing both the numerator and denominator by the same number.
As a result the Browns’ saving expressed as a fraction is:
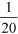
This fraction can also be expressed as a percentage. To do this it is useful to understand that the fraction 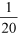 is the same as the division sum 1 ÷ 20.
is the same as the division sum 1 ÷ 20.
The percentage can therefore be calculated as follows:
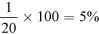
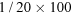
The Browns’ water savings could also have been calculated directly:
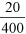
Activity 6 Fractions and percentages
What saving would result from their strategy to reduce their water use for baths and showers to two-thirds of the normal use?
You can calculate the reduced daily amount of water used for baths and showers as follows:
This will be 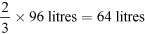 .
.
The saving is therefore 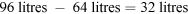 .
.
An alternative way to get to this answer is to recognise that if the water use is reduced to  of its normal value, the saving must be
of its normal value, the saving must be 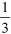 of the normal value.
of the normal value.
Copy Table 3 into your notebook and enter your answers there.
Question 1
Now express the water saving as a fraction and a percentage of the family’s initial total average daily water use.
Question 2
Now consider the savings from their third strategy. What fraction of their normal use for flushing the toilet will be saved, and what is this saving as a percentage of the normal use for flushing the toilet?
What total daily saving results from their strategy of reducing their water use for flushing the toilet? Express your answer in litres and as a fraction and a percentage of the initial total daily water use.
| Use of water | Fraction | Percentage |
| outside use | 5% | |
| bath/shower | ||
| flushing toilet |
Comment
Question 1
As a fraction this saving is 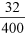 or
or 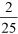 and as a percentage
and as a percentage 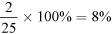 .
.
Question 2
By putting a 1-litre ‘save-a-flush’ bag in the cistern, the amount of water used per flush is reduced from the normal 10 litres to 9 litres, a saving of 1 litre.
This saving as a fraction is 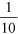 and as a percentage
and as a percentage 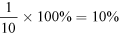
- The daily saving will be
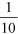 of the daily use for flushing the toilet, so this is
of the daily use for flushing the toilet, so this is  .
.
This saving can again be expressed as a fraction of the total daily use as 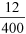 or
or 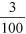 and as a percentage
and as a percentage 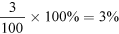 .
.
| Use of water | Fraction | Percentage |
| outside use | 5% | |
| bath/shower | 8% | |
| flushing toilet | 3% |
Activity 7 Comparing fractions and percentages
Which of the two ways (fractions and percentages) used in the table above to express the relative savings makes them easiest to compare?
Comment
The completed table shows that the savings are much easier to compare when expressed as percentages. The savings on water for toilet flushing is lowest – 3% of the total use – followed by outside use (5%), and the largest saving, of 8%, is for baths and showers. The savings are not so easy to compare when expressed as fractions. For example, can you tell from a quick glance which of 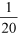 ,
, 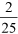 and
and 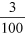 is the largest and which is the smallest?
is the largest and which is the smallest?
If you would like to find out more about using fractions and percentages you could take a look at the free badged open course Succeed with maths – Part 1 [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] .
