3.4.1 Try some yourself
Activity 24
For each of the following calculations make suitable rough estimates before doing the calculation on your calculator and check the result.
(a) 22.12 ÷ 4.12
(b) 0.897 × 10.00345
(c) 1009 × 23.789 × 278.98
(d) (12.98 + 14.87 + 63.098) ÷ 12.54
Answer
You may have worked out a ball-park figure rather than under and over estimates or you may have used different estimates. This does not matter as long as you can check on whether your calculator answer is what you would expect.
(a) Overestimate: 24 ÷ 4 = 6
Underestimate: 20 ÷ 5 = 4.
Answer = 5.368932039.
(b) Overestimate: 1 × 11 = 11
Underestimate: 0.8 × 10 = 8.
Answer = 8.97309465.
(c) Overestimate: 1010 × 24 × 300 = 1010 × 7200 = 7272 000
Underestimate: 1000 × 20 × 270 = 5400 000
Answer = 6696 385.117
(d) Overestimate: (13 + 15 + 64) ÷ 10 = 9.2
Underestimate: (12 + 14 + 63) ÷ 13 = 89÷ 13
 7
7Answer = 7.252631579.
Activity 25
You are helping a friend, Al, who is preparing a base for a new garage. He needs to purchase ready-made concrete from a local supplier. The concrete is sold in units of cubic metres so he needs to calculate how much to order.

The plan of the proposed garage is shown in the diagram above. Following advice from a builder the base is to have a thickness of 200 mm. Al's estimate for concrete required is given below.
volume = length × width × thickness
volume = 6.56 × 4.68 × 2.00
volume = 61.4016 cubic metres
Hence volume of concrete needed is 61 cubic metres, to 2 s.f.
Make a rough estimate of what you would expect the answer to be. Are you happy with Al's calculation?
Answer
Rough estimate = 7 × 5 × 0.2 ![]() 7 cubic metres.
7 cubic metres.
Al's estimate = 61 cubic metres which seems rather large, by a factor of about ten, so you should not be happy with his estimate.
He has said that 200 mm = 2 m whereas he should have used 0.2 m: he should have divided 200 by 1000 rather than 100. (There are 1000 mm in 1 m.)
Activity 26
Suppose a friend has worked out the price of carpeting some stairs with carpet which costs £4.50 per square metre.
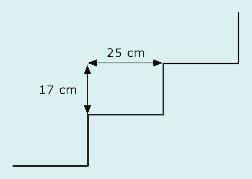
The stairs are in three flights of ten, and each step requires 25 cm for the tread and 17 cm for the rise. The stair width is nearly one metre. There are also landings to be carpeted of length 1.2 m and 5.4 m, both one metre wide. By estimating what the answer should be, and then working through what he has done, check the calculation below for your friend.
Each stair 25 + 17 = 42
Ten stairs 42 × 10 = 420
Three flights of stairs 420 × 3 = 1260
Landings 1.2 + 5.4 = 6.6
Total length 6.6 + 1260 = 1266.6
Cost £4.50 × 1266.6 = £5699.7
Answer
£5699.7 seems a lot for a stair carpet.
Estimate of answer: Length needed for one step ![]() 0.2 + 0.2
0.2 + 0.2 ![]() 0.4m.
0.4m.
Length needed for 10 stairs ![]() 10 × 0.4 = 4 m
10 × 0.4 = 4 m
So length needed for 30 stairs ![]() 4 × 3 = 12 m.
4 × 3 = 12 m.
Landings need ![]() 1 + 6
1 + 6 ![]() 7m
7m
So total length needed = 12 + 7 = 19 ![]() 20 m.
20 m.
So cost would be about 20 × 5 = £100 which is a lot less than £5699.70.
The stairs are measured in cms and the landings are measured in metres. So in calculating ‘total length’ your friend has added numbers of different units. The cost of the carpet is in pounds per metre, so it is sensible to convert centimetres to metres for the calculation. Measuring in metres gives 6.6 + ![]() = 19.2 metres. Your friend might need a safety margin so he should buy 20 metres at a cost of 20 × £4.50 = £90.
= 19.2 metres. Your friend might need a safety margin so he should buy 20 metres at a cost of 20 × £4.50 = £90.
