The Pulfrich pendulum: an experimental investigation
Introduction
In this experiment you will be investigating a phenomenon known as the Pulfrich pendulum effect. As you might guess, it involves a swinging pendulum, and was first described in 1922 by a German physicist called Carl Pulfrich.
This is a very simple effect to demonstrate, and to try it for yourself you need just three things:
- a length of thin string or thread at least two metres long
- a weight to tie on the end (e.g. a bunch of keys or a small kitchen utensil)
- a pair of sunglasses
You might also like to collect the equipment you will need for the later part of the experiment:
- a tape measure
- a long stick or ruler
- some Blu tack or similar
- a pencil
The pendulum should be quite long, so you might use a drawing pin to attach the top to the ceiling, and have the weight at the other end near the floor.
Try to set it up in a position where you will be able to stand back and watch it swinging from a reasonable distance – say two metres or more.
Set the pendulum swinging ‘across ways’ as you view it from position A; in other words, not towards and away from you, but from side to side, as shown in Figure 1.
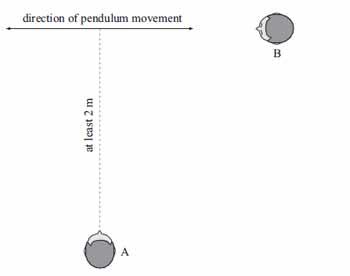
Figure 1 Plan diagram of the required set-up. The effect is observed from position A. Use position B to check alignment of the pendulum.
From position B, make sure that it really is swinging in a straight line, with no tendency to follow a circular path. Now, here’s the interesting part!
Stand in position A and hold up the sunglasses so they cover just one eye - but keep both eyes open.
As you watch the swinging pendulum, using one ‘bright’ eye and one ‘dim’ eye, the straight side-to-side motion should seem to have changed into an elliptical swing.
In other words, the pendulum should appear to be tracing an oval path.
This will still work perfectly well if you wear spectacles – just hold the sunglasses in front of one lens.
However, if your spectacles are of the photochromic variety that change shade according to the amount of light falling on them, holding the sunglassesi n front of one lens will reduce the light falling on that lens and therefore make it lighter.
The end result may be that you do not see the effect (or such an obvious effect). In that case, you are recommended to put the sunglasses behind one lens of your spectacles.
A small proportion of people don’t see this effect. If you are unlucky at first, persevere for a minute or two, but if the pendulum still seems to be swinging straight, you should try it on someone else, and get them to describe what they see.
An explanation
There are two key factors that give rise to this phenomenon. The first is that the brain derives an impression of an object’s distance by comparing the views seen by the two eyes.
The second important element is that the photoreceptors in the eyes respond more sluggishly when the scene is less bright. The reason for this is that the receptors (rods and cones) cannot initiate an action potential until sufficient photopigment has been bleached by the light.
This takes longer when there is less light, so if we are viewing a moving object, the image that the brain has to deal with will be just a little out of date.
Our slightly slower visual response in poor lighting is recognised in the game of cricket, where one sometimes hears ‘bad light stopped play’. In failing light conditions a fastmoving cricket ball could hit a player, while he believed it still to be a little way off.
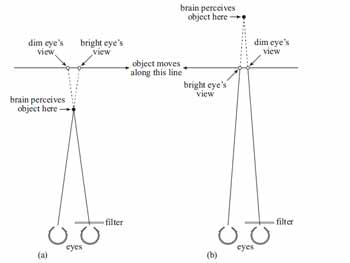
Figure 2 A moving object, viewed with one eye brighter than the other, appears either in front of or behind the true track, depending upon direction of motion.
Figure 2 shows the effect of giving one eye a bright view and the other a dim view of a moving object.
As explained, the dim eye will produce a slightly delayed signal, compared with the bright eye (which itself must take a finite time to respond). How the brain interprets the pair of ‘out-of-kilter’ images depends upon which way the object is moving.
As can be seen, movement in one direction (Figure 2a) results in the object appearing closer than it actually is, while the opposite movement (Figure 2b) makes it seem further away.
The size of these errors depends upon how fast the object is moving; clearly, if it were crawling along, the out-of-date view would be almost identical to the actual position.
A swinging pendulum moves at its fastest in the middle of the swing, and comes to a momentary stop at the ends, where it changes direction.
Consequently, when viewing a pendulum with one eye dimmed, the apparent distance shift will be greatest in mid-swing and zero at the ends of the swing. The result is that the pendulum seems to follow an elliptical path.
You should be able to see why changing the sunglasses to the other eye would make the ellipse seem to be traced in the opposite direction. You can try that out with your pendulum, to confirm that it is the case.
There is one rather sad part to this interesting effect: Pulfrich was blind in one eye, so he was never able to observe the phenomenon that bears his name and interested him so much.
The first part of the experiment that we are asking you to do involves measuring the time lag and details are given below.
Once you have calculated your first time lag you certainly won’t find it difficult to measure one or two more. So we are asking you to take the study a little further, to discover something new for yourself.
Taking the measurements
You will need to make a number of measurements, which are indicated in Figure 3, and then carry out some simple calculations which are described in the next section.
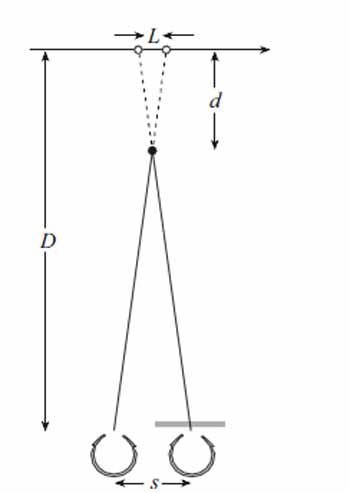
Figure 3 Measurements to be taken for the experiment. D is the distance from viewer to actual pendulum position; d is the distance from actual to apparent position (at mid point); s is the separation of the eyes. L is calculated from the other measurements; it is the distance by which the dim eye’s view lags the position seen by the bright eye.
As you can see, you will need to measure how far your eyes are from the pendulum, where the pendulum seems to be in relation to where it really is, and the distance between the centres of your pupils.
For the calculations that follow it is important that all the measurements are made in the same units. In other words, you should not measure D in metres, d in centimetres and s in millimetres.
The final result will not be affected by the choice of units, but you will find centimetres the most convenient. Be as accurate as possible – for example don’t record the inter-pupillary distance as 7 cm if it is really 6.8 cm (i.e. 68 mm).
Most of the measurements are made more easily on someone else, but if you want to measure your own eye separation it is possible to do so, looking in a mirror.
Ideally, to make the measurement of D and d as accurate as possible, the viewer’s eyes should be on the same level as the pendulum weight.
You can achieve this comfortably by making the pendulum rather shorter, and viewing it from a low chair. Alternatively, you (or your participant, if you test someone else) can sit (or lie on the stomach) on the floor.
To locate the apparent position of the pendulum you will need some form of pointer. You can use your ingenuity here, but a possible technique is to use a stick or long ruler.
The stick is rested on the floor, one end in front of the viewer and the other under the pendulum. At the pendulum end some ‘Blu-Tack’ is used to attach a pencil, pointing vertically upwards.
The pencil should be long enough to reach close to (but not touching) the pendulum when it is at rest.
When observing the Pulfrich effect, the stick is used to move the pencil nearer or further from the viewer, until it seems that the pendulum at the near point of the ellipse is swinging directly above it.
Measuring from the pencil position to the true midpoint of the swing will give the value of d.
The size of d will depend upon how fast the pendulum is swinging, so as the pendulum slows down d will get smaller. That means the pointing process has to be carried out fairly quickly, before the pendulum has changed speed appreciably.
It is certainly easier to carry all this out with two people – one to view and the other to keep the pendulum swinging – but the pendulum will tend to keep going longer if it is long, and if the weight is not too light.
When you set the pendulum swinging you will of course pull it to one side; make sure you pull it out the same distance each time. If you change the width of the swing you will change the speed at the centre of the swing.
So it is important to use the same width of swing for each experiment that you do.
Before you pack everything away at the end of the experiment, there are two more measurements you will need to make. The first is the width of swing, mentioned above.
Record the distance from the mid-point (where the pendulum comes to rest) to the position it reached at the extremity of its swing to one side. Let us call this distance W. (You will notice that this is actually half the swing width.)
The other measurement you need is the length of the pendulum. That should be the distance from where it is attached, down to the middle of its weight. Let us call this distance P.
At the end of each experiment you should have recorded values of d, D, s, W and P.
Calculations
The calculations you will have to carry out are not difficult, although a calculator will be needed. A little of the background to the mathematics and physics will be explained, for those who like to see where figures come from, but it is not essential that you understand it all.
You will notice in Figure 3 that the ‘lines of sight’ from each eye cross over, to form two triangles: a small one at the top, pointing down, and a larger one, based on the eyes, pointing up.
Although the triangles are different in size (and one is upside down), they are actually exactly the same shape.
They are therefore what are known as similar triangles. As a result, corresponding measurements are exactly in proportion.
For example, if the width of the large triangle (the distance between pupils) happened to be one quarter of the triangle’s length (the distance from eyes to crossing point), the same would apply to the smaller triangle. So, using this fact, we can write:
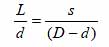
and, therefore:
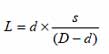
This equation can be used to find L.
What you have calculated so far is the distance that the dim eye’s image lags behind the bright, but our intention is to determine the time lag of the slower, dim eye.
That is easily calculated, if we know how fast the pendulum is moving. Then we can use the simple equation:
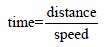
Or, in our case:
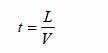
where t is the time lag we want to find and V is the speed. The speed we need is the speed at the centre of the pendulum’s motion.
To perform that calculation, all we need to do is find the value of V. That is something that can be calculated from the dimensions of your pendulum (you will remember measuring its length and how far you pulled it to one side).
Unfortunately, the mathematics of a pendulum is not quite as simple as the earlier material, so we will just present the result here.
The speed at the centre of the swing is given by
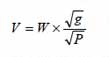
where g is the acceleration due to gravity and W is the half-width of the swing that you have already measured.
The value of g is 981 cm s–2. It is important to use a value that matches the units you used in all the measurements. If, for example, you made the measurements in metres, then g must be expressed as 9.81 m s–2. Your calculations will not be too far out if you take the value of g to be 1000 cm s–2 or 10 m s–2.
So you are now in a position to calculate both L and V. To find the time lag, divide L by V. The answer will be the time, in seconds, by which the slow eye lags the faster, bright eye. You will find that it is a rather small figure.
You will need to carry out the same calculation for each of the experiments you do.
Find out more
Demonstration of Pulfrich Effect at the State Fair
Rate and Review
Rate this video
Review this video
Log into OpenLearn to leave reviews and join in the conversation.
Video reviews
Julie Jones - 11 March 2016 4:11pm
Great, but the above video does NOT show the Pulfrich effect...what it does show is 5 minutes of someone driving through some rather nice scenery.
OpenLearn Moderator - 16 March 2016 3:16pm
Hi,
Many thanks for letting us know - I've asked the team to link to something more suitable.
Best wishes
OpenLearn Moderator
OpenLearn Moderator - 16 March 2016 3:26pm
Hi,
Thanks for pointing out that the video wasn’t as clear an example of the effect as it could have been. We’ve taken the opportunity to improve the video showing the effect – and included it on the page.
Best wishes
OpenLearn Moderator