Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
What are waves?
What are waves?

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

4 Graphical representation of waves

As you learn more about waves and the different situations in which they occur you will see that it is convenient to represent waves graphically. We can plot a wave as a graph in two ways: as a function of distance and as a function of time. It is important to appreciate the difference between them and the properties of the wave that are represented in both.

Taking the example of a stone splash in a pond, if we take a snapshot of the wave on the surface of a pond at a fixed point in time, such as a freeze frame of Figure 2, and plot the vertical position or displacement of a point at the surface as a function of distance from the point where the stone was dropped, we have a wave represented as a function of distance:

Described image
Figure 5  A generic graph showing the properties of a wave that is plotted as a function of distance.
Show description|Hide description

This figure shows a graph. The x-axis is labelled distance, but no tick marks or units are shown. The y-axis is unlabelled apart from an arrow at the top.

A red sine curve – that is, a smoothly curved line rising and falling regularly – starts at the origin, and rises first to a high point labelled ‘peak’. It then falls to an equal distance below the x-axis, labelled trough, and rises again to another peak, and falls to another trough and so on. There are three peaks and two troughs.

Amplitude is shown in three places on the graph. First, a dashed line has been drawn from the first peak back to the y-axis, horizontal to the x-axis, and the distance from the origin to the point where the dashed line crosses the y-axis is labelled ‘amplitude’. Second, the distance from the x-axis to the low point that represents the second trough is also labelled ‘amplitude’. Third, the distance from the x-axis to the top of the third peak is labelled ‘amplitude’. These measurements are all identical in length.

Wavelength is also illustrated on the graph in several places. The distance from the first peak to the second peak is labelled ‘wavelength’. The distance from the first trough to the second trough is labelled ‘wavelength’. Also, a number of dashed lines run horizontally, each joining a point the curve falling from the first peak to the first trough with an equivalent point on the curve joining the second peak to the second trough. These dashed lines are labelled ‘alternative measurements of wavelength’. These measurements are all identical in length.

Figure 5  A generic graph showing the properties of a wave that is plotted as a function of distance.

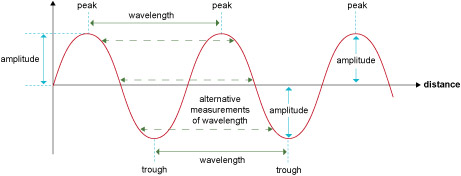
In the case of the stone splash, the vertical axis represents the displacement of the water from the undisturbed water line, but as you encounter waves in other situations, you will come across different units on the vertical axis such as, for example, intensity or voltage. For this reason the vertical axis is unlabelled in Figure 5, as it represents the generic case of any wave that is plotted as a function of distance.

When a wave is plotted with distance on the horizontal axis, the distance from one peak to the next, or one trough to the next, marks one complete cycle, and this distance is known as the wavelength. Note that the peak to peak or trough to trough are merely the easiest places to measure the wavelength or the period. Any full cycle will do, as shown by the dashed lines in Figure 5. In other words, you can measure the wavelength or period as the distance between any pair of equivalent points, that is, points where the wave has the same 'height' and is changing in the same way (i.e. the gradient is either positive for both points or negative for both points).

The maximum vertical displacement of the wave from the undisturbed surface is the amplitude.

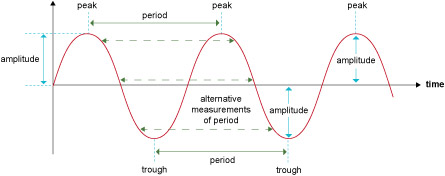
We can also plot a wave as a function of time. Using the same example of the stone splash in a pond, if we now focus on a point on the surface at a fixed distance from where the stone was dropped, such as one of the green points in Figure 3, and plot the vertical displacement as a function of time, we have a wave represented as a function of time:

Described image
Figure 6  A graph showing the properties of a wave that is plotted as a function of time
Show description|Hide description

This figure shows a graph that is almost identical to that in Figure 5. The x-axis is labelled time, but no tick marks or units are shown. The y-axis is unlabelled apart from an arrow at the top.

A red sine curve – that is, a smoothly curved line rising and falling regularly – starts at the origin, and rises first to a high point labelled ‘peak’. It then falls to an equal distance below the x axis, labelled trough, and rises again to another peak, and falls to another trough and so on. There are three peaks and two troughs.

Amplitude is once again shown in three places on the graph. First, a dashed line has been drawn from the first peak back to the y-axis, horizontal to the x-axis, and the distance from the origin to the point where the dashed line crosses the y-axis is labelled ‘amplitude’. Second, the distance from the x-axis to the low point that represents the second trough is also labelled ‘amplitude’. Third, the distance from the x-axis to the top of the third peak is labelled ‘amplitude’. These measurements are all identical in length.

However, this graph does not show wavelength. Because the wave is now plotted as a function of time, this graph illustrates the measurement of the period of the wave.

Period is illustrated on the graph in several places. The distance from the first peak to the second peak is labelled ‘period. The distance from the first trough to the second trough is labelled ‘period. Also, a number of dashed lines run horizontally, each joining a point the curve falling from the first peak to the first trough with an equivalent point on the curve joining the second peak to the second trough. These dashed lines are labelled ‘alternative measurements of period. These measurements are all identical in length.

Figure 6  A graph showing the properties of a wave that is plotted as a function of time

When a wave is plotted with time on the horizontal axis, the time taken from one peak to the next, or one trough to the next, marks one complete cycle, and this time is known as the period. As in the previous graph, the maximum vertical displacement of the wave from the undisturbed surface is the amplitude.

So the definitions of wavelength and period are rather similar. The wavelength is a distance and refers to points separated in space but measured at a fixed instant in time; the period is a time interval and refers to instances separated in time but measured at a fixed point in space.