2.1.1 Try some yourself
Activity 14
Measurement of a ceiling gives a length of 6.28 m and a width of 3.91 m.
(a) Make a rough estimate of the area of the ceiling (the length times the width).
(b) If one litre of paint covers roughly 11 square metres, roughly how much paint will you need to cover the ceiling?
Answer
(a) Rounding to the nearest metre gives 6 m × 4 m, so the area is about 24 square metres.
(b) Divide by the area covered by each litre (11 square metres). Rounding this to 10 square metres means that about
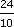= 2.4 litres are needed. So two and a half litres is a good estimate.
Activity 15
Supposing a calculator was used to determine the area of the ceiling and the amount of paint needed in Question 1, and gave the answers:
(a) 24.5548 square metres;
(b) 270.1028 litres.
Do the answers agree with your rough estimates? Do the answers seem reasonable? If not, can you see what has gone wrong?
Answer
The first answer agrees with the rough estimate of 24 square metres. But the 270.1028 litres does not. Try to imagine 270 litres. It is an enormous quantity of paint. What has happened is that the area was multiplied by 11, instead of divided by 11.
Activity 16
During the summer season various music festivals are held. Glastonbury rock music and Cambridge folk are two of the larger events. Such large-scale events have planning implications for the organisers in respect of catering facilities, waste disposal and toilet/shower facilities.
Suppose that you are an organiser of the camping arrangements at such an event and you have sold 56 432 tickets in advance. So you know that a large crowd of people will be on location at your festival for at least three days. You will need to estimate how much field space you require and how many toilet/shower units you should hire.
This is a planning problem and sensible estimates are necessary in order to provide suitable facilities. A list of the assumptions that you may need to consider whilst solving this problem is given below.
Most tent accommodation is shared by two people.
A typical tent measures 3 metres by 2.5 metres and 2.2 metres high.
Each tent requires a boundary of about 1 metre spacing surrounding it, to allow for tent pegs etc.
Roughly one-fifth of the people will use the shower facilities in the peak demand time, between 7 am and 10 am.
Each shower takes 5 minutes.
On average people make about four visits per day to the toilet, spread evenly throughout day and night.
Each toilet visit lasts roughly 2 minutes.
Make the following estimates:
(a) Round the number of advanced ticket sales to one significant figure. Hence estimate the number of tents.
(b) What area does each tent require in the field? So what is the area of field required?
(c) Estimate the number of minutes of showering which are likely between 7 am and 10 am. How many minutes are there between 7 am and 10 am? About how many shower cubicles are needed?
(d) How many toilet visits are there per 24 hours? How long is spent in total? So estimate how many toilet cubicles are required.
(e) Consider the catering requirements. How many meals and cans of drink might be needed?
Answer
(a) 56 432
60 000 (1 s.f.).-
If 2 people share a tent then an estimate of the number of tents is
-
60 000 ÷ 2 = 30 000 tents.
(b)
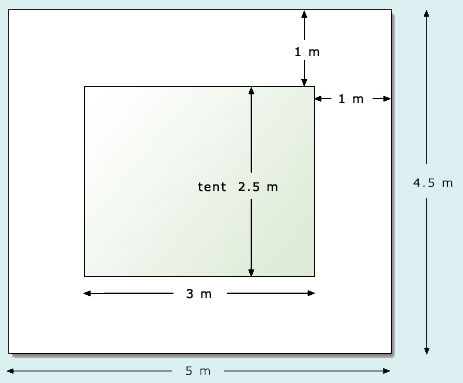
Area required by each tent with boundary is
-
Area = length × breadth
-
= 5 m × 4.5 m
-
= 22.5
20 square metres. -
So area required is 30 000 × 20
600 000 square metres. (c) One fifth of people will use the shower, i.e. 60 0000 × 1/5 = 12 000 people.
-
Each shower takes 5 minutes, hence the number of showering minutes is
-
12 000 × 5
60 000 minutes. -
Number of minutes between 7 am and 10 am = 3 × 60 = 180 minutes
200 minutes. -
Number of shower cubicles needed
60 000 ÷ 200 300 cubicles. (d) Number of toilet visits is number of people times number of visits per day
-
60 000 × 4 = 240 000 units.
-
Number of toilet minutes
240 000 × 2 480 000 minutes. -
Number of minutes in 24 hrs
24 × 60 1440 1500 minutes. -
Number of toilet cubicles needed is
-
480 000 ÷ 1500
320 toilet cubicles. (e) You need to estimate here how many meals per day and how many cans of drink each person may require, e.g. 3 meals and 6 drinks.
-
So number of meals
60 000 × 3 180 000 but since some people may not eat 3 meals per day you might order only 150 000 meals. -
Number of drinks
60 000 × 6 360 000 but if you want to offer a choice of drinks you might order more, especially if you expect the weather to be very hot so people are very thirsty …
Activity 17
Answer the following questions:
(a) For each of the following, make a rough estimate first; then find the answer using your calculator.
(i) 75 450 − 27 654
(ii) 676 295 + 984 122
(iii) 16.859 × 4.962
(iv) 3.512 ÷ 720.5
(b) Some of the following answers are wrong, as the result of mistakes in keying the calculations into the calculator. Find which are the wrong ones, without using your calculator.
(i) 631 − 529 = 6102
(ii) 13 726 + 4317 = 18 043
(iii) 1066 × 45 = 7470
(iv) 1066 ÷ 0.45 = 23.688 889 (rounded to six decimal places)
Answer
(a)(i) Rough estimate: rounding to the nearest thousand:
75 450
75 000, 27 654 28 000.So 75 450 − 27 654
75 000 − 28 000 = 47 000.Or you may have rounded to the nearest 10 000, to give
80 000 − 30 000 = 50 000.
The exact value is 47 796.
(a)(ii) Rough estimate: rounding to one significant figure (i.e. to the nearest 100 000):
676 295
700 000, 984 122 1000 000So 676 295 + 984 122
700 000 + 1000 000 = 1700 000.The exact value is 1660 417.
(a)(iii) 16.859 × 4.962
17 × 5 = 85.The exact value is 83.654 358.
(a)(iv) 3.512 ÷ 720.5
4 ÷ 700. This may not be very helpful. Another approach is to spot that, if you round 3.512 to 3.5, you can divide top and bottom by 7: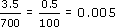
(Don’t worry if you didn’t spot this. It doesn’t matter as long as you found a rough estimate by some means.)
The calculator gives 0.004 874 3928 (to eight significant figures).
(b)(i) Wrong.
631 − 529
600 − 500 = 100, not 6000.
(b)(ii) Right.
13 726 + 4317
14 000 + 4000 18 000, so it could be right.
(b)(iii) Wrong.
1066 × 45
1000 × 50 = 50 000, not 7000.
(b)(iv) Wrong.
1066 ÷ 0.5
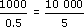= 2000, not 20.One way of noticing there must be a mistake is to notice that dividing by a decimal number between 0 and 1 always gives an answer larger than the original number.
Activity 18
Find a rough estimate for each of the following and then evaluate on your calculator. In each case round your answer to two significant figures.
(a) 0.086 + 219.2
(b) 0.050 − 0.048
(c) 457.3 − 64.5 + 302.4
(d) 441.7 × 5.2
(e) 53.4 × 70.9 ÷ 22.2
(f) 217.5 + 60.3 × 17.7
(g) (1285 − 329) × 0.023
Answer
(a) Estimate: 0.086 + 219.2
0 + 220 = 220. The calculator gives 219.286.
(b) 0.050 − 0.048
0.05 − 0.05 = 0. This is not good enough – all significant figures are lost! You cannot estimate this roughly – use all the given figures: 0.050 − 0.048 = 0.002. There is only one significant figure in the answer, so you cannot round it to two significant figures.
(c) 457.3 − 64.5 + 302.4
460 − 60 + 300= 400 + 300 = 700.
The calculator gives 695.2
700, to 2 s.f.(Notice that, although there only appears to be one significant figure here, the answer was rounded to two; both the 7 and the first 0 are significant.)
(d) 441.7 × 5.2
400 × 5 = 2000.The calculator gives 2296.84
2300, to 2 s.f.
(e)
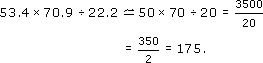
The calculator gives 170.543 2432
170, to 2 s.f.
(f) 217.5 + 60.3 × 17.7
200 + 60 × 20= 200 + 1200 = 1400.
The calculator gives 1284.81
1300, to 2 s.f.
(g) (1285 − 329) × 0.023
- (1300 − 300) × 0.02 = 1000 × 0.02
= 1000 ×
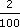= 20.The calculator gives 21.988
22, to 2 s.f.