3.6.1 Try some yourself
Activity 33
The population of a village is 5481. Round this:
(a) to the nearest thousand people;
(b) to the nearest hundred people.
Answer
(a) 5481 rounded to the nearest thousand people is 5000 people.
(b) 5481 rounded to the nearest hundred people is 5500 people.
Activity 34
Suppose you went shopping with £30 cash and discount coupons to the value of £3.60 for various items that you intended to buy (such as £1 off a giant tin of biscuits). You did a rough estimate of your shopping bill by adding up the items you were buying (without taking the coupons into account) and it came to £25. Roughly how much cash would you expect to have left after paying the bill?
Answer
The amount of cash in pounds you will have left is roughly 30 + 3.60 − 25, or equivalently 30 − 25 + 3.60, i.e. about £8.60, or £9 (more roughly).
Activity 35
Suppose you are one of four people buying some joint presents for a family of five. The presents cost £2.15, £3.02, £2.99 and two at £2.50. Estimate your share of this cost.
However, when you used your calculator to calculate your share:
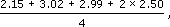
using the calculator you got the answer £9.41. Why doesn’t this answer make sense? Investigate what you might have done wrong.
Answer
The cost of the presents is roughly £2 + £3 + £3 + £5 (= 2 × £2.50), which is £13. So your share is roughly 13/4 = £3.25. Another way of estimating is to notice that all the five presents cost two or three pounds, so the total cost will not exceed about 5 × £3 = £15. Therefore each of the four people's share of the cost must be less than £4 (since 4 × £4 = £16). In any event, £9.41 is clearly wrong.
What you have done is to calculate 2.15 + 3.02 + 2.99 + 2 × 2.50 ÷ 4, which your calculator interprets as 2.15 + 3.02 + 2.99 + (2 × 2.50 ÷ 4). You need to work out 2.15 + 3.02 + 2.99 + 2 × 2.50 first and then divide this total by 4. This can be achieved using brackets: (2.15 + 3.02 + 2.99 + 2 × 2.50) ÷ 4. (The exact answer is £3.29.)
Activity 36
Suppose you were sharing 28 biscuits among 5 children and you did the calculation 28 ÷ 5 = 5.6. How many biscuits would you give each child?
Answer
If you rounded 5.6 up to 6 and gave the answer as 6, you would not have enough biscuits, since 6 × 5 = 30 and you only have 28 biscuits.
If you rounded down and gave 5 biscuits each, you would have three over, since 5 × 5 = 25. (You might eat these yourself or keep them to give as rewards later.)
You might be able to break a biscuit into two and so answer 
, which gives 
, leaving half a biscuit for you.
Whatever answer you gave, it must make sense in the context of sharing biscuits.
Activity 37
Suppose you were considering purchasing a patterned carpet, priced at £15.75 per square metre, for the room shown in the diagram below which a friend has measured for you. It might be appropriate to use rounded values.
(a) What degree of accuracy do you think would be most appropriate?
(b) Estimate the cost of the carpet.
(c) Would your estimate alter if the required carpet is from a roll 4 metres wide?
Answer
(a) The measurement should be rounded up for practical purposes, since otherwise the carpet may be too small for the room. An accuracy to the nearest 0.1 metre would be sufficient. Then the length of the room would be rounded to 3.6 metres and the width to 2.8 metres. (If the room is not exactly rectangular you might add on more for safety.)
(b) To estimate the area and hence the price, you might round even more to 3.5 × 3. These values give an area of 10.5 square metres. So round to 10. Round the price to £16 per square metre. So the estimate is £160.
(c) If the carpet has a roll-width of 4 metres you have two options, depending upon whether the direction of the pattern on the carpet is important to you. This means you may need (approximately) either a 3 metre length (12 sq metres) or a length of 3.5 metres (14.5 sq metres). So you will need another 2 or 4 sq metres. This adds on about £30 or £60 giving an estimate of £190 or £220 respectively.
Activity 38
Find a rough estimate for each of the following calculations and then evaluate them on your calculator.
(a) 0.91 + 2.8956
(b) 0.6841 + 0.3692 + 0.2381
(c) 40.89 × 5.28
(d) 58.98 × 82.93 ÷ 4.89
(e) (4839 − 876) × 0.0891
Answer
(a) Estimate: 1 + 3 = 4. Calculation 3.8056.
(b) Estimate: 0.7 + 0.4 + 0.2 = 1.3. Calculation 1.2914.
(c) Estimate: 40 × 5 = 200. Calculation 215.8992.
(d) Estimate: 60 × 80 ÷ 5 = 960. Calculation 1000.247 73.
(e) Estimate: 4000 × 0.1 = 400. Calculation 353.1033.
Activity 39
Answer the following questions:
(a) Estimate a rough total for the supermarket bill below.
| margarine | 69p |
| milk | 22p |
| sugar | 49p |
| sausages | 92p |
| eggs | 87p |
| bread rolls | 97p |
(b) Dave earns £784 per month. Make a rough estimate of how much he earns per year.
Answer
(a) Round the numbers to 70 + 20 + 50 + 90 + 90 + 100 = 420 pence or £4.20. So the bill should be a bit more than £4. (In fact the exact total is £4.16.)
(b) 784 rounds to 800. So in a year Dave earns about £800 × 12, which is £9600. (In fact he earns exactly £9408 a year.)
Activity 40
Answer the following questions:
(a) Estimate the area of a strip of earth measuring 27 m by 3 m, which is to be grassed, in order to order the turf.
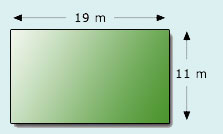
(b) Make a rough estimate of the area of carpet tiles needed for the rectangular hall illustrated below.
Answer
(a) Round 27 up to get 30. So the area
30 × 3 = 90 square metres.(b) Round the numbers to get 20 × 10. So the area
20 × 10 = 200 square metres. (Since the exact answer is 19 × 11 = 209 square metres, you’d be in a bit of a mess here if you just bought 200 square metres. This example illustrates that in many practical situations it is safer to overestimate than underestimate.)