2.3 The mass, composition and structure of the Sun
The Sun is massive. We can work out the mass of the Sun by measuring the size and period of the orbit of a planet such as Jupiter or the Earth. Sir Isaac Newton’s laws of gravity can then be used to calculate just how heavy the Sun would need to be to keep the planet moving around its orbit. And when you do this you find that the Sun is incredibly massive – over 1 000 times the mass of Jupiter, the biggest planet in the solar system, and about 330 000 times the mass of the Earth.
Although the Sun is very massive indeed, it is also very large. Remembering that the Sun is approximately 100 times the diameter of the Earth, this means that it has one million times the volume. If it were made of the same type of materials as the Earth the Sun’s mass would also be one million times greater, but in fact it is only one-third of this, meaning that the density of the Sun is more similar to that of Jupiter – a gas giant made up of mostly hydrogen and helium.
-
What do you think this tells you about the composition of the Sun?
-
The fact that Jupiter and the Sun have similar densities suggests that the Sun is made up of gases such as hydrogen and helium, rather than the rocks and metals that make up the Earth. By looking in detail at the spectrum of light that the Sun emits, astronomers can detect the unique signature of the elements that make it up. Indeed the element helium is so named because it was first discovered in the Sun’s atmosphere by spectral analysis.
Viewing the Sun in different wavelengths can also reveal remarkable details of the surface structure. The following video shows images of the Sun taken in different wavebands, including visible light, ultraviolet and X-rays. For more information, visit the NASA SDO website at: https://sdo.gsfc.nasa.gov/gallery/main/item/785

This rich surface structure and the activity that you saw in Activity 3 suggest that the interior of the Sun also has a complex and dynamic structure. This NASA image shows a cutaway view of the internal structure of the Sun.
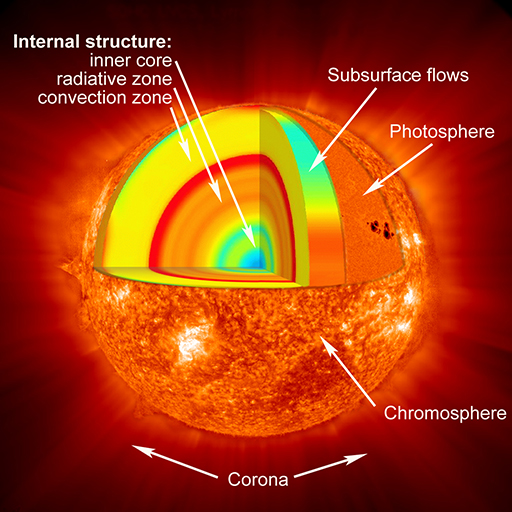
Full resolution image available here [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)]
