Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Succeed with maths: part 1
Succeed with maths: part 1

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

1 Puzzles and real-world maths

You probably use maths every day without realising, from working out how much change you might receive, to how long a journey might take, to solving puzzles. You’re going to start by looking at some puzzles.

You may be wondering what puzzles have to do with solving real problems. First of all, they introduce you to working logically and systematically, which is an important general technique that is used often in mathematics. Second, they introduce the idea that sometimes you have to find a ‘way in’ to a puzzle by trying different things. By doing this, it doesn’t mean that you can’t do the puzzle or that you’re getting it wrong!

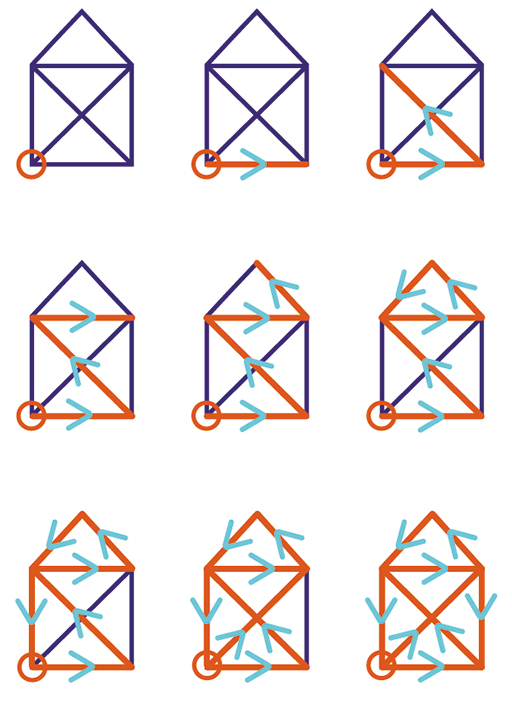
  • Can you draw the shape given in Figure 1 without taking your pen off the page or going over any lines more than once? Have a go on a piece of paper now.

    A square with two lines going to the diagonally opposite corner. A triangle sits on top of the square from the corners.
    Figure 1 Line drawing puzzle
    Show description|Hide description

    A line drawing showing a square with a cross through it with the two lines going to the diagonally opposite corner. A triangle then sits on top of the square from the corners.

    Figure 1 Line drawing puzzle

  • Figure 2 shows a sequence of images which gives one solution to solving the puzzle.

    The solution to the puzzle. Detailed description in Long description link below image.
    Figure 2 The solution to the line drawing puzzle
    Show description|Hide description

    Step-by-step drawing to show one possible solution to the puzzle in a series of nine images.

    The first image shows the complete shape outlined in blue with a circle in the bottom left hand corner of the square to mark the starting point.

    The second image shows an arrow pointing from the circle to the bottom right hand corner of the square and the line connecting these two corners has now turned orange.

    The third image has replicated the second image but also has an arrow pointing from the bottom right hand corner of the square to the top left hand corner of the square. This line has now also turned orange.

    The fourth image has replicated the third image but also has an arrow pointing from the top left hand corner of the square to the top right hand corner of the square. This line has now also turned orange.

    The fifth image has replicated the fourth image but also has an arrow pointing from the top right hand corner of the square to the top of the triangle. This line has now also turned orange.

    The sixth image has replicated the fifth image but also has an arrow pointing from the top of the triangle to the bottom left corner of the triangle/top left corner of the square. This line has now also turned orange.

    The seventh image has replicated the sixth image but also has an arrow pointing from the bottom left corner of the triangle/top left corner of the square to the bottom left corner of the square (starting point). This line has now also turned orange.

    The eighth image has replicated the seventh image but also has an arrow pointing from the bottom left corner of the square (starting point) to top right corner of the square. This line has now also turned orange.

    The ninth and final image has replicated the eighth image but also has an arrow pointing from the top right corner of the square to the bottom right corner of the square. This line has now also turned orange meaning the whole line drawing is orange.

    Figure 2 The solution to the line drawing puzzle

    But you don’t have to do it exactly like this! Provided you start with one of the bottom corners and end with the other, you can’t really go wrong.

    This type of puzzle relates to a part of maths that involves studying networks. A real-life example of this type of puzzle could be: if a salesperson had to visit five towns, what order should they do it to travel the least total distance overall?

It quite often happens in mathematics that what started out as very abstract topics with no practical use, later turn out to be extremely important in science or technology. Just because it is difficult to see a use at the time does not mean that there will not be some important practical development later!

Activity 1 Organising a dinner party

Timing: Allow approximately 15 minutes

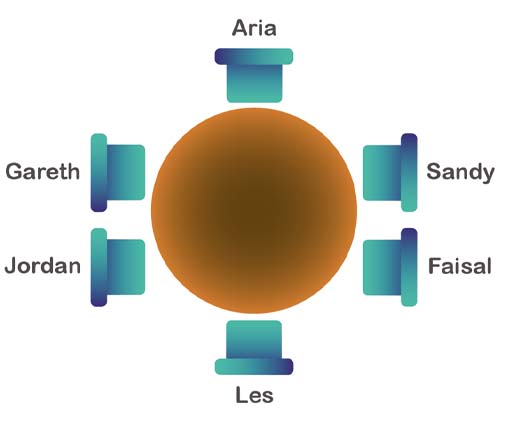
Sandy and Les are having some friends round for dinner. There will be six of them sitting round their circular table, but unfortunately not all their friends get on well and so they want to arrange a seating plan that will keep everyone happy.

Read the conversation between Sandy and Les and then work out how they can seat their guests.

Sandy
Faisal doesn’t get on with Gareth, so we can’t put them next to each other. And Jordan used to go out with Aria, but they split up, so they can’t be next to each other.
Les
Don’t put Jordan directly opposite Aria either – they’ll just glare at each other! Just sit them with one person between them. And as the hosts, we can’t sit together. But I’d better be nearest the kitchen so I can go to get more drinks for people.
Sandy
Oh, and we can’t put Gareth next to you then – it’s too near the radiator and he’ll moan it’s hot all the time. And we can’t put Jordan and Gareth with their backs to the window as they’ll want to keep an eye on those fancy cars they have.
But I’d really like to sit next to Aria – I’ve not had a good chat to her for so long.
 

Try it! See if you can seat everybody and stick to the rules Les and Sandy have. You might find it helpful to draw out the plan of the table so you can try different ideas. Hints are given below if you get stuck.

Table with 6 chairs. A window and kitchen are also labelled. Full description in Long description link.
Figure 3 Dinner party table layout
Show description|Hide description

Sketch of a table with six chairs round it – two chairs on the left, two chairs on the right, one at the top of the table and one at bottom. The kitchen is indicated to be at the bottom of the image and there is a window on the right.

Figure 3 Dinner party table layout

Hint 1

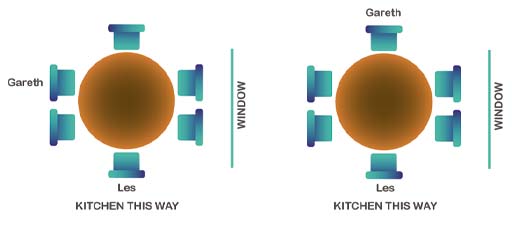
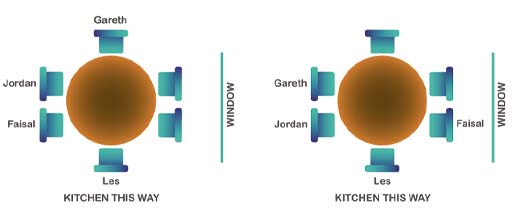
There’s one person who can only be in one place – put them in first. Then think about which places Gareth can be in.

Comment

You should have put Les at the foot of the table as he wants to be closest to the kitchen.

Figure 4 then shows the two places that Gareth could sit.

Table plan options with Les and Gareth seated. Full description in Long description link below image.
Figure 4 Possible places Gareth can sit
Show description|Hide description

Two sketches of the table and chairs arrangement side by side.

The first sketch shows Gareth positioned on the left side in the seat furthest away from the kitchen. It also shows Les seated in the chair at the foot of the table closest to the kitchen.

The second sketch shows Les again at the foot of the table closest to the kitchen, but this time Gareth has been positioned directly opposite him at the top/head of the table.

Figure 4 Possible places Gareth can sit

Hint 2

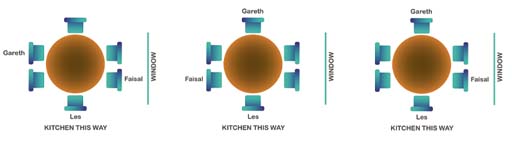
For each of the instances given in Figure 4 (Hint 1), where can Faisal be? Remember you need to leave two seats together for Aria and Sandy to sit together.

Comment

Faisal can’t sit next to Gareth. So Figure 5 shows where Faisal could sit (remembering to leave two seats next to each other for Sandy and Aria).

Table plan options with Les, Gareth and Faisal seated. Full description in Long description link.
Figure 5 Possible places Faisal can sit
Show description|Hide description

Three sketches of the table and chairs arrangement side by side.

The first sketch shows Gareth positioned on the left side in the seat furthest away from the kitchen, Les seated in the chair at the foot of the table closest to the kitchen and Faisal next to Les on the right hand side with their back to the window.

The second sketch shows Les again at the foot of the table closest to the kitchen, but this time Gareth has been positioned directly opposite him at the top/head of the table and Faisal next to Les on the left hand side.

The third sketch shows Les again at the foot of the table closest to the kitchen, Gareth directly opposite him at the top/head of the table and Faisal next to Les on the right hand side.

Figure 5 Possible places Faisal can sit

Hint 3

Now think about where Jordan can sit. Remember, he doesn’t want his back to the window and he can’t be seated next to Aria.

Comment

In Figure 5, Jordan has to be in the seat on its own as two seats need to be left spare together for Aria and Sandy to sit next to each other. Because Jordan also can’t have his back to the window it means the seating arrangement can’t be the third sketch in Figure 5.

So the options then become:

Table plan options with Les, Gareth, Faisal and Jordan seated. Full description in Long description link
Figure 6 Possible places Jordan can sit
Show description|Hide description

Two sketches of the table and chairs arrangement side by side.

The first sketch shows Les at the foot of the table closest to the kitchen, Gareth positioned directly opposite him at the top/head of the table, Faisal next to Les on the left hand side and Jordan in between Faisal and Gareth.

The second sketch shows Les seated in the chair at the foot of the table closest to the kitchen, with Faisal next to him on his right hand and Jordan next to him on his left. Gareth is then next to Jordan on Jordan’s left.

Figure 6 Possible places Jordan can sit

Hint 4

Now you need to place Sandy and Aria. Remember, Aria can’t be opposite Jordan, and Sandy can’t be next to Les.

Answer

The final seating plan must be:

Table plan options with all guests seated. Full description in Long description link below image.
Figure 7 The final seating plan
Show description|Hide description

Sketch of a table with six chairs round it – two chairs on the left, two chairs on the right, one at the top of the table and one at bottom.

Les is seated at the foot of the table and Aria is directly opposite. Faisal is sat on Les’s right and has Sandy next to him. Sandy is then also sitting next to Aria.

On Les’s left is Jordan, who is also sitting next to Gareth.

Figure 7 The final seating plan

The hints to solve Activity 1, and the order of doing things, may have been quite different to how you approached it. Maybe you figured out where you could put Sandy first, or Aria and Jordan? Maybe you did some trial and error? That’s quite normal! There’s often not just one best approach, but there are some good strategies to use – and that’s what you’ll look at next.