3.1 Parts of the whole – decimal numbers

An example of a decimal number is 1.5, said as one point five. The point in the middle is called the decimal point and is used to separate the whole numbers from decimal parts of the number. The 5 in 1.5 represents the part of a whole number.

To understand how the decimal part of a number works, you can start by extending the place values you have already to the right, making each one 10 times smaller. This allows you to represent numbers that are parts, or have parts of whole numbers. These are known as decimals numbers. This gives a place value table that looks like that shown in Table 2.

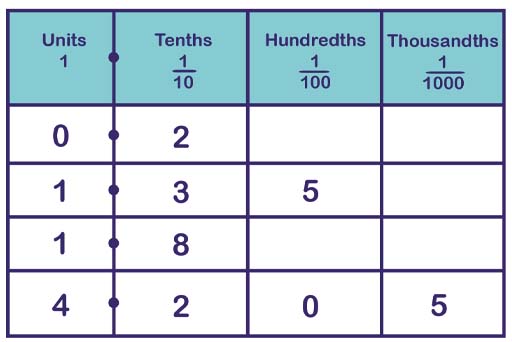
The next place value table shown in Figure 9 shows a decimal point added in. This is where the whole numbers are separated from the parts of whole numbers.

Figure 9 A place value table showing decimal numbers

Show description|Hide description

This is a table with four columns and five rows. The first column is headed Units, the second Tenths, the third Hundredths, and the fourth Thousandths. In the second to fifth rows there is a decimal point between the Units column and the Tenths column.

In the first row the first column contains 0, the second 2, the third and fourth columns are blank. This is a representation of 0.2.

In the second row the first column contains 1 and the second 3 and the third contains 5, the fourth column is blank. This is a representation of 1.35.

In the third row the first column contains 1 and the second contains 8. The third and fourth columns are blank. This is a representation of 1.8.

In the fourth row the first column contains 4, the second 2, the third 0 and the fourth 5. This is a representation of 4.205.

Figure 9 A place value table showing decimal numbers

The numbers shown in the table (Figure 9) are:

• no units and two-tenths, written as 0.2
• one unit, three-tenths and five hundredths, written as 1.35
• one unit and eight-tenths, written as 1.8
• four units, two tenths, zero hundredths and five thousandths, written as 4.205.

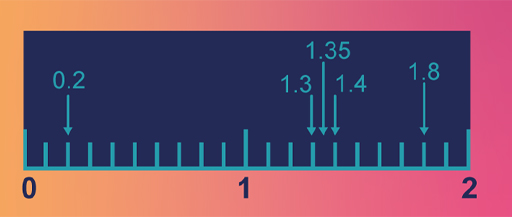
As well as using a place value table you can also show decimal numbers on a number line. This may help you to visualise decimal numbers. Take a look at the number line in Figure 10. The intervals between the whole numbers (or units) have each been split into ten equal intervals, each one is therefore 10 times smaller than a unit, so each of these is a tenth. If each tenth had then been split into ten equal intervals, these new intervals will be hundredths, since there will be 100 of these intervals in a whole unit.

Figure 10 A number line

Show description|Hide description

A number line from 0 to 2 marked out in intervals of 0.1. Arrows point to the places where 0.2, 1.3, 1.35. 1.4 and 1.8 sit on the number line.

Figure 10 A number line

The number line shows the following numbers expressed in decimal form:

• two-tenths, written as 0.2
• one unit and three-tenths, written as 1.3
• one unit, three-tenths and five-hundredths, written as 1.35
• one unit and four-tenths, written as 1.4
• one unit and eight-tenths, written as 1.8.

Now have a go at these questions, which give you practice at identifying the different place values.

You’ve already used some of the four basic operators, such as multiplication and addition in the new vehicle problem in Section 2, but now you’re going to look at all these basic operators in turn, as they are all fundamental to maths and everyday calculations.