1.1 The process of adding and subtracting
You might like to watch this next video before attempting Activity 1, which will guide you through the process of adding and subtracting fractions.
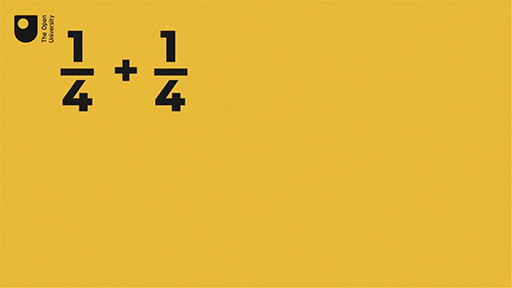
Transcript
Activity 1 Adding and subtracting fractions
Have a go at these questions, showing your answers in the simplest form or mixed number where relevant. Remember to make sure before you add or subtract to make the denominators the same.
- a.
Hint: Are both fractions out of the same number of parts? Remember as always to show your answer in the simplest form.
Answer
Both the given fractions are eighteenths, so they can be added together directly:
To simplify to , divide the numerator (top) and the denominator (bottom) by 6.
- b.
Hint: both fractions are eighths, so again you can add them directly.
Answer
The answer is:
If this is converted to a mixed number, the answer is:
- c.
Hint: can you find equivalent fractions for each given fraction that all share the same denominator? What number can be divided by both 6 and 7?
Answer
This sum involves sixths and sevenths, which are different types of fraction. However, you can change both into forty-seconds, since both 6 and 7 evenly divide into 42. So, by multiplying by 7 and by multiplying by 6.
Thus, the sum is .
- d.
Hint: try adding the whole numbers first, and then add the fractional parts together.
Answer
In this calculation you can add the whole numbers first (2 + 3 = 5) and then add the fractions. First, you must convert each fraction into twenty-fourths, as both 3 and 8 divide exactly into 24. So, the sum is:
- e.
Answer
Both the fractions are sixteenths so you subtract straightaway:
- f.
Hint: first ensure both fractions have the same denominator.
Answer
You need both fractions to be out of the same number of parts (the denominators).
Since , you can multiply the top and bottom of by 3 to make the equivalent fraction of and then carry out the subtraction.
Therefore:
- g.Two children were squabbling about chocolate. Josie had been given of a bar by her aunt and of a bar by her dad. Tim had been given a bar by his mum and by his friend. All the original bars were the same size. Was Josie or Tim given more chocolate, or were they given equal amounts?
Hint: add up what fraction of a bar each child had. To compare your two fractions, cancel each to its lowest terms.
Answer
Josie had of a bar. To add these, we need to put them over a common denominator. The common denominator is 12. So becomes . cancels down to of a bar.
Tim has of a bar. The common denominator is 6. So becomes . cancels down to of a bar.
Therefore, Josie and Tim had the same amount of chocolate.
Well done – you’ve completed your first activity involving carrying out calculations with fractions! In the next activity you will look at a more practical application of fractions.
