5 Rules for negatives
As you first learn how to work with negative numbers and develop your skills, a number line is very helpful – but it can sometimes be very tedious and not very convenient!
Remembering a few basic rules can be a great help and so can a ‘common sense’ check using some of the practical examples.
Rule 1
If you are adding two numbers that have the same sign, like (–4) + (–3) , momentarily ignore the signs, and add the numbers together. Then place the sign in front of the sum.
You can think of (–4) + (–3) as 4 + 3, which equals 7. Since both numbers were negative, you place a negative sign in front of the answer: (–4) + (–3) = –7. You can verify this using a number line.
Common sense check
If you are £4 in debt, (so ‘-4’) and then you owe another £3 (so ‘-3’) you will still end up in debt, and more in debt than you started! Your answer must be compatible.
Rule 2
If you are adding two numbers that have different signs, such as (–8) + 2, you momentarily ignore the signs. Then subtract the numbers and place the sign of the ‘larger’ number in front of the difference.
You ignore the signs in (–8) + 2 and subtract 8 − 2, which equals 6. Since the ‘larger number’ is 8, and it has a negative sign in front of it, the overall answer is also negative: (–8) + 2 = –6.
Common sense check
If you are £8 in debt (‘-8’) and someone gives you £2 (‘+2’) then you can see that you will still be in debt, but less in debt than you started out. So the answer is still negative, but the size of the debt is less.
Rule 3
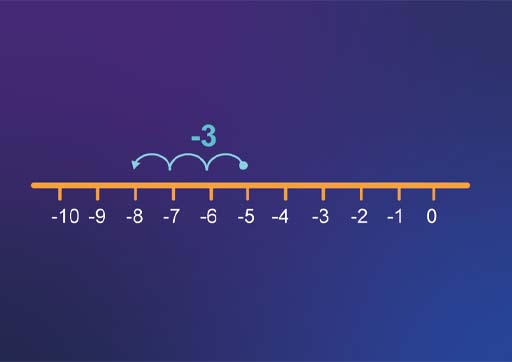
If you are subtracting a positive number, like (–5) − 3, then rewrite it as addition of the negative number and then use the rules for addition: (–5) − 3 = (–5) + (–3) = –8.
Common sense check
Debt works here too! If you are £5 in debt (-5) and then you have to pay out £3 (so you subtract 3) – you end up more in debt.
To help you visualise this example, look at the number line in Figure 13.
Rule 4
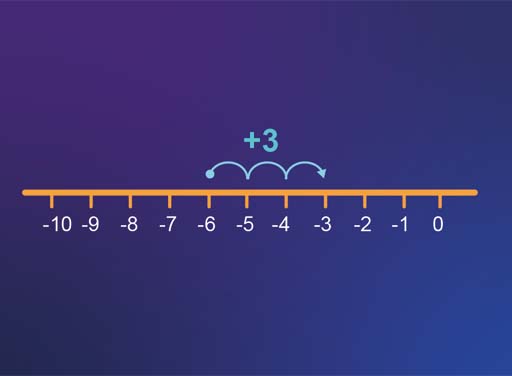
If you are subtracting a negative number, such as (–6) − (–3), then rewrite it as addition of the positive number and then use the rules for addition: (–6) − (–3) = (–6) + 3 = –3.
Common sense check
Using debt as an example again – if you are £6 in debt, and someone cancels (= takes away) £3 of the debt (so – (-3)), then you are left with £3 debt.
Check out the number line in Figure 14 to see the addition.
Of course, if you feel comfortable adding and subtracting negative numbers without these rules, there is no need to use them.
Use the rules in this next activity to help you to decide if you find them useful.
Activity 5 Adding and subtracting negative numbers using the four strategies
Try these questions using the four strategies above.
- a.18 + (–3)
Hint: look at Rule 2 above.
Answer
- a.You are adding two numbers with different signs. Ignore the signs and subtract the numbers 18 − 3 and use the sign from the larger number in the answer. So, 18 − 3 = 15.
- b.(–21) + (–6)
Hint: look at Rule 1 above.
Answer
- b.You are adding two numbers with the same sign. Ignore the signs and add the numbers, 21 + 6, and put back the signs from the numbers. So, (–21) + (–6) = –27.
- c.32 − (–8)
Hint: look at Rule 4.
Answer
- c.Rewrite as addition of a positive number, 32 + 8. So, 32 − (–8) = 40.
- d.(–25) − (–4)
Answer
d.Rewrite as addition of a positive number, –25 + 4. Then follow rule 2. Ignore the signs and subtract the numbers 25 − 4, and use the sign from the larger number in the answer.
(–25) − (–4) = –21
It’s important to get to grips with carrying out addition and subtraction involving negative numbers on paper or in your head to get a real understanding of how to do this. It will also help if you keep the rules to hand and practise your new skills. Fortunately, you can also turn to a calculator. You can try this in the next section.