2.1 Rotations of a triangle
Let us discuss the notion of symmetry through the example of a triangle. This one is very regular, in that all its sides have equal length and they all meet at equal angles of 60 degrees.
This is called an equilateral triangle. Because it is so regular, this triangle possesses symmetries.
Question 1
Can you see any symmetries upon immediate observation?
Answer
You may observe lines of reflection from a corner to the midpoint of the opposite edge. You may also note that if you rotate the triangle, it doesn’t take a full rotation to come back to the same position.
You will now explore the symmetries of this triangle more closely. Start by preparing a triangle to play around with.
Activity 1 Creating your triangle
Take a piece of paper and cut out an equilateral triangle. Label the lower left corner C1, the lower right corner C2 and the top corner C3. Repeat these labels on the back side. Label the front side of the paper with the letter A and the back with the letter B.
You can find an example here [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] . (If you print this out, make sure it’s double-sided and properly lined up for cutting out.)
Now, take another piece of paper. Draw an equilateral triangle the same size as before, and label the corners P1, P2 and P3, again starting from the lower left corner and proceeding anticlockwise. This time though, write the labels outside the triangle. No need to cut this one out.
You can find an example of this second triangle here.
Place the cut-out triangle on top of the drawn triangle, with the top side (A) facing up and the corners matching the ones underneath, so that C1 is at position P1, C2 at position P2 and C3 at position P3. This will be the starting position for some experimentation.
Now, pick up the triangle and turn it around anticlockwise, until it is occupying the same space again, with all edges and corners meeting an edge and corner on the paper underneath. How far do you have to rotate the triangle for this to happen?
Answer
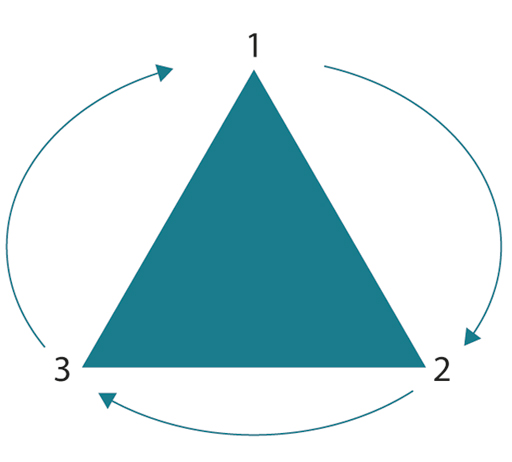
You have to rotate it 1/3 of the way round, which is 120 degrees (a full rotation being 360 degrees). Once you have turned it by this amount, the three corners have moved around, and the triangle looks the same as before. This is what geometry calls a symmetry: a transformation that, when performed on an object, leaves the object unchanged.
The corners were labelled to help you describe precisely what happens when the triangle is rotated. Compare the labels in the corners of your triangle with those on the underlying paper. If you labelled everything as described, you should find that corner C1 is now at position P2, corner C2 has moved to position P3, and corner C3 has moved to position P1. This can be written symbolically as 1 → 2, 2 → 3 and 3 → 1, or also as a cycle. This gives us a nice shorthand notation for the effect of the rotation.
Based on the results so far, what will happen when you rotate your triangle anticlockwise by a further 120 degrees?
Answer
Following corner C1 as it moved to P2 in the first rotation, it now moves to P3. This result can be written as 1 → 3. Note that this corresponds to two steps on the cycle diagram above. Check that this also happens for the other two corners, which means that 2 → 1 and 3 → 2.
Rotating the triangle a further 120 degrees – a total of 360 degrees, considering all three rotations – puts all corners back in their original positions.
This triangle can be said to have a ‘threefold rotational symmetry’ – there are three different orientations of the triangle where the object looks the same, corresponding to rotations of 0, 120 and 240 degrees.
What happens then, if you rotate by 120 degrees in the clockwise direction? How could you write that in terms of the cycle diagram?
Answer
This rotation is 1 → 3, 2 → 1, 3 → 2.
There are two ways to see this. You either go backwards on the cycle diagram, reversing all the arrows (corresponding to rotating in the opposite direction), or you consider the fact that rotating clockwise by 120 degrees is the same as rotating anticlockwise by 240 degrees, corresponding to two steps on the cycle diagram.
Mathematicians call the structure formed by these rotations a ‘group’, which is a collection of transformations with the following properties:
You can combine any two transformations to obtain another transformation from the same group.
For any transformation, there is a transformation in the group that reverses it.
Groups provide the fundamental mathematical structure for the description of symmetries. The strength of mathematical group theory lies in its application to any system with transformations that demonstrate these properties.
Question 2
If the equilateral triangle is rotated anticlockwise by 120 degrees, which transformation reverses this?
Answer
A clockwise rotation of 120 degrees. (Of course, the same result can be obtained with a further anticlockwise rotation of 240 degrees.)
So, have the symmetries of this triangle been fully explored? Not quite. You’ll look next at reflections.