3 Measuring infinity
Are all infinite things the same size? The answer, as you’ll see, is no! Mathematician Georg Cantor showed how you can think about sizes of infinity, and how you can measure them.
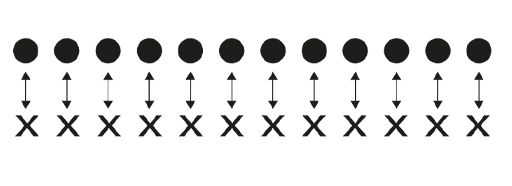
In order to unlock the way to count infinite sets of things, it helps to look closely at how you count finite sets. Consider the picture below. Are there as many dots as crosses?
You can check by pairing them up.
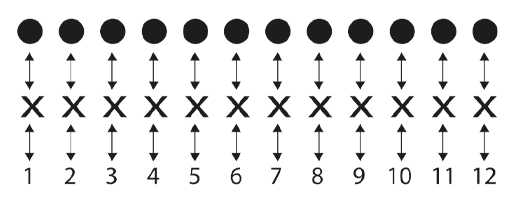
Another way to check is counting the set of dots, then counting the set of crosses. This is essentially the same as pairing them up with counting numbers.
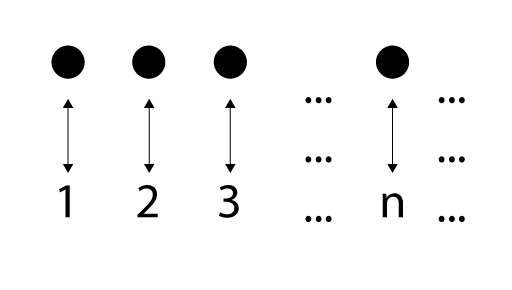
In the same way, you can ‘count’ infinite sets by matching them up with the counting numbers. For example, if you have an infinite set of dots in a line you could pair them up with the counting numbers, like this:
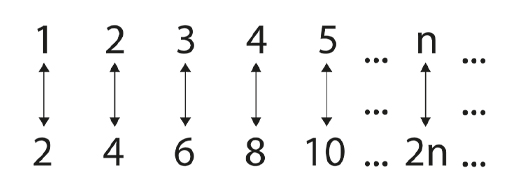
By specifying a ‘map’ in which each number, n, is paired with its double, 2n, you can formally demonstrate the claim from Section 2 – that there are as many even numbers as counting numbers. This map is illustrated by the following figure.
Activity 1
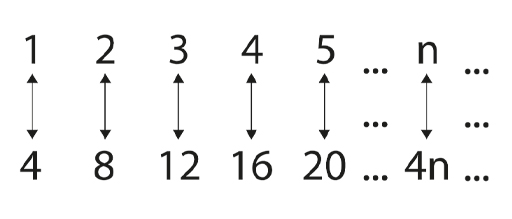
Can you show there are as many multiples of 4 as there are counting numbers? What should n be mapped to, in order to show this?
The size of the set of counting numbers can be shown to be the ‘smallest’ infinity, and you have just seen that the set of even numbers and the set of odd numbers are the same size. Other sets which have the same size are:
- all whole numbers both positive and negative
- all the prime numbers
- all numbers that can be written as fractions (this includes whole numbers as they can be written as a fraction over 1).
The last set in that list might’ve been unexpected – you shall see a proof of it shortly.
However, numbers which can’t be written as fractions do exist. The number π (pi) is a well-known example. Once you add in all the numbers like π and , then you make a set which is bigger than the counting numbers. You can no longer pair up the members of this set with the counting numbers.