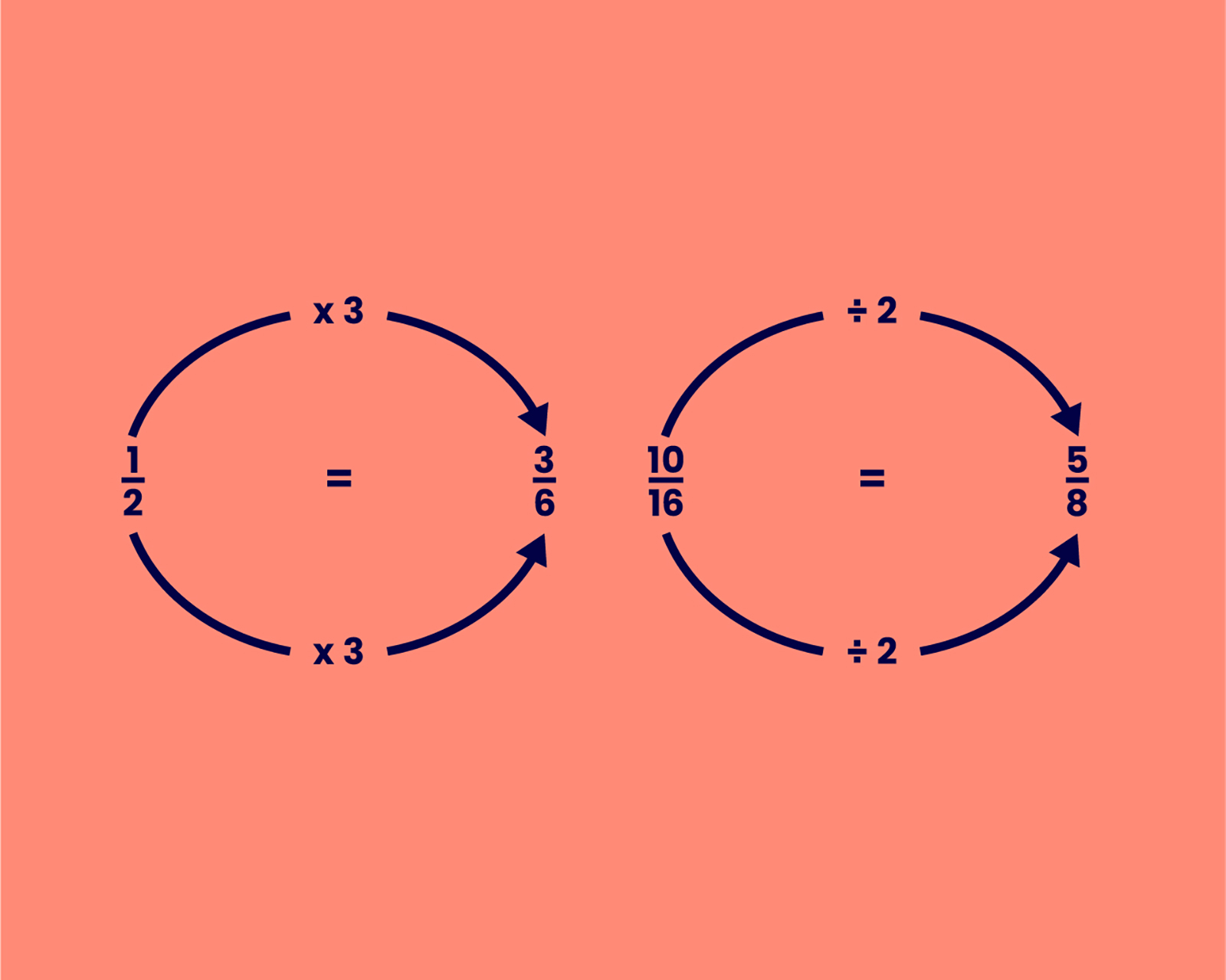
7.4 Equivalent fractions
We can produce equivalent fractions by multiplying or dividing both the top (numerator) and the bottom (denominator) of the fraction by the same number.
In order to simplify a fraction, divide the top and bottom of the fraction by a common factor (a number that divides exactly into both the top and bottom numbers).
A fraction is in its simplest form when the numerator and denominator cannot both be further divided by any number other than 1.
Simplest form = simplest equivalent fraction
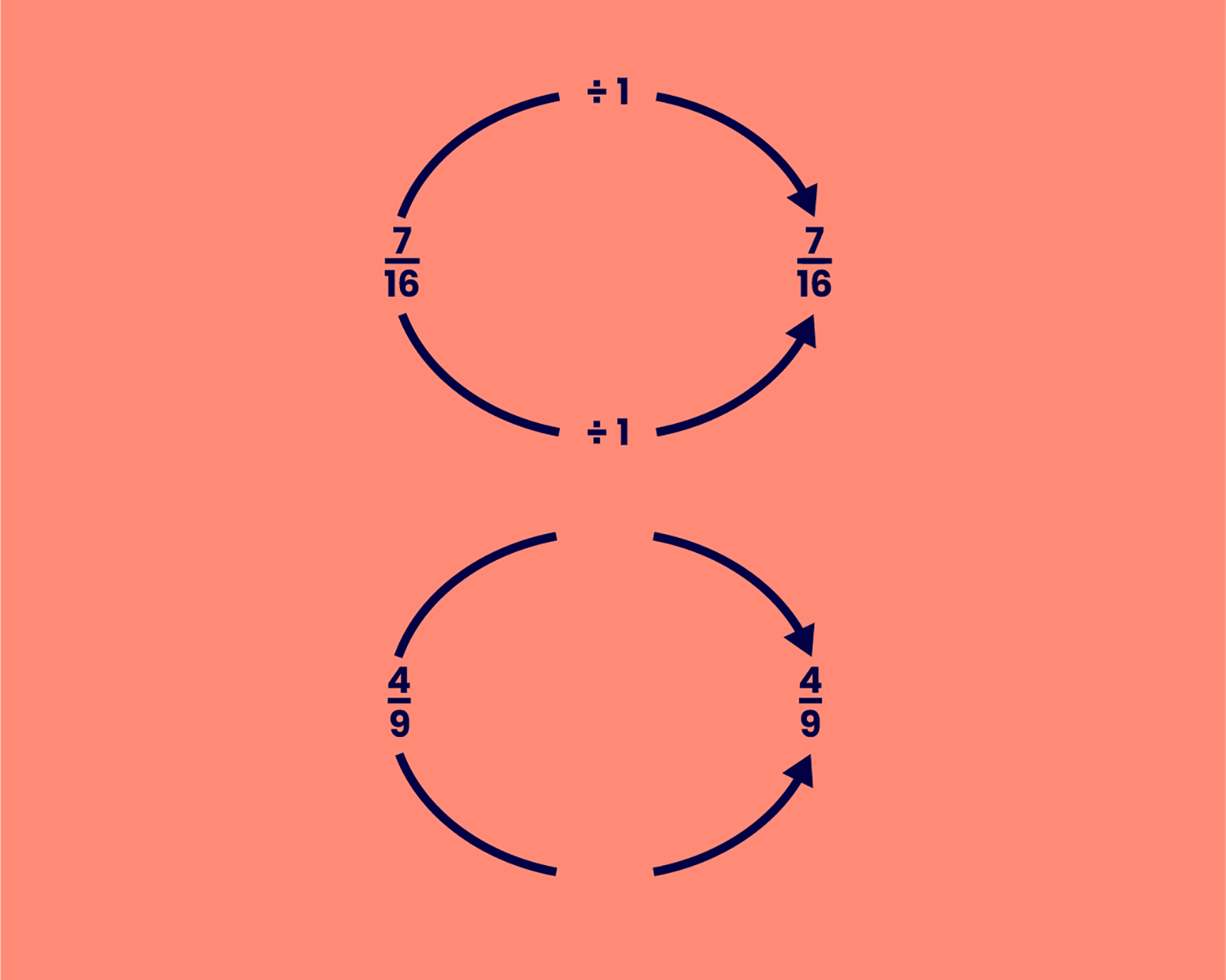
Some numbers will not cancel down. Prime numbers will not divide by any number other than 1 e.g. 7,11,13,17, etc. The numerator and denominator may not be divisible by the same number.
Examples include: , ,
7 is a prime number and will not divide by anything other than 1. 4 and 9 do not have a common factor and therefore the fraction is in its simplest form.
Activity 19: producing equivalent fractions
1. Complete the following equivalent fractions:

2. Simplify the following fractions whenever possible:
=
=
=
=
=
=
Answer
1.
a) = =
b) = =
c) = =
2.
=
cannot be simplified as 9 and 14 have no common factor.
=
=
=
cannot be simplified as 2 and 13 are both prime numbers.