1.3.5 Energy from fission
Nuclear power is based on the energy that is released each time a uranium nucleus undergoes fission.
Energy and mass
In nuclear reactions, the energy released can be understood from Einstein’s most famous equation:
E = mc2
Here E is energy; m is mass and c the speed of light.
This shows that there is a clear equivalent relationship between mass (m) and energy (E). The speed of light is shown as c and it is has a large value. Light travels at 300 million ms−1. In fact, the speed of light is squared in the equation giving an even bigger number, 90 million billion! (The units of this would be (ms−1)2 but we don’t need to worry about this.) Suffice to say, to work out the amount of energy bound up in a mass we multiply the mass by a huge number – a small mass converts into a very large energy.
This equation holds true if you can convert mass into pure energy – although this is easier said than done! One place that this conversion takes place is within the nucleus, so if we can master nuclear reactions we can tap into this energy.
Binding energy
Imagine you had a marble and knew its mass was 5g. If you then received a bag of 20 identical marbles and were asked the total mass of these marbles you may reason that it is 20 × 5g = 100g. And you would be correct!
Mass of 20 marbles = 20 × mass of one marble
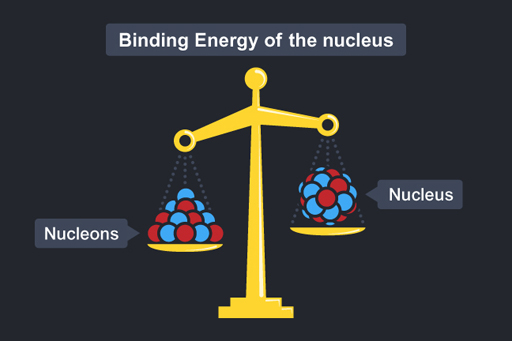
Now imagine you had a nucleon and knew it was a certain mass m (protons and neutrons have pretty much the same mass) and you were then asked the mass of a nucleus containing 20 nucleons. You may reason, as before, that its mass would be 20m. But in fact the mass of the nucleus would be less than this – the mass of the nucleus is less than the mass of the constituent parts! This is represented in Figure 16.
Mass of a nucleus containing 20 nucleons < 20 × mass of one nucleon
The difference in mass is called the mass defect.
Mass defect = Mass of separate nucleons − Mass of nucleus
Where has the missing mass gone? It has been converted into energy – this is called the binding energy of the nucleus. The binding energy is associated with the forces that bind the nucleus together.
From E = mc2
Binding energy = mass defect × c2
Different nuclei have differing amounts of binding energy. In fission, a large nuclei is split into smaller parts. The total mass of these parts may be lower than the initial large nucleus. This difference in mass is due to the difference in binding energy between the nuclei and is released as energy.
Energy from fission
The mass of the fission products and the three neutrons is less than of the U-236, although the number of nucleons is the same. This missing mass is released as energy – generally taken away by the fission products, the neutron and the gamma radiation.
The energy released from one fission is small but with many nuclei, the energy adds up to far exceed the amount from the equivalent chemical reactions. The fission of 1kg uranium provides a million times more energy than the burning of 1kg of coal. Fission can provide a great deal of heat energy.
It was this knowledge, before the ability to harness this energy had been developed, that led nuclear physicist Leo Szilard, in 1934, to speculate about planned experiments that, if successful, would lead to:
Power production … on such a large scale and probably with so little cost that a sort of industrial revolution could be expected; it appears doubtful for instance whether coal mining or oil production could survive after a couple of years.
Next week, you will be learning more about the use of fission as an energy source to generate electricity.
In the next section is a video outlining the development of working nuclear reactors.