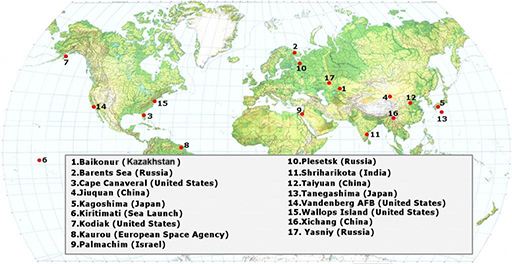
3.2 Location of launch sites
You should now appreciate how difficult it is to send a rocket into space. But what about the location of the launch site on Earth? Take a look at Figure 11 and then complete Activity 5.
Activity 5 Launching a rocket
a.
Equator
b.
North Pole
c.
Atlantic Ocean
d.
Pacific Ocean
e.
South Pole
The correct answer is a.
Discussion
At the Equator, Earth is rotating at nearly 1700 kilometres per hour (km/h). If the rocket is launched half-way between the Equator and the North or South Pole, the speed is reduced by nearly 500 km/h. This makes it harder for the rocket to escape Earth’s gravity.
a.
Russia and the USA
b.
India and China
c.
Japan and the European Space Agency
The correct answer is a.
Answer
The largest number of launch sites are in Russia and the USA.
How can you calculate the acceleration of a rocket from the launch pad to the edge of the Earth’s atmosphere? To do this, you need to use one of Newton’s Laws. Here, you need the Second Law which relates force (F), mass (m) and acceleration (a) as shown in Equation 1.
You need to change the mass of the rocket – in this case, say 40 tonnes – into kg. So, the mass m = 40 × 1000 kg = 40 000 kg = 4 × 104 kg.
Question 4 in Activity 5 provided an approximate value of the thrust of such a rocket, that is, F = 800 000 N = 8 × 105 N.
Now, if you rearrange Equation 1 and substitute in these values, you get Equation 2.
Here you can see that the derived units of newtons (N) have been broken down into the fundamental units of kilograms (kg), m and s. The numerical value in Equation 2 is just over twice the value of the acceleration due to gravity (g) near the surface of the Earth, which is 9.81 m/s2 (or m s–2). It means that, for every second you fall under Earth’s gravity, you travel another 9.81 m/s faster.
Now you’ve calculated how to get to the ISS. But how does it stay up in Earth’s orbit?