4 Sodium D-lines and the hydrogen atom

Energy levels are demonstrated in the context of a sodium lamp in Video 3. Watch it now and then do Activity 4.

Download this video clip.Video player: Video 3

Show transcript|Hide transcript

Transcript: Video 3 Sodium D-lines.

HELEN:

So in the last experiment, we absolutely established that light can behave as a wave, but now we're going to show you something that shows that also lights can behave as a particle. So here I have an experiment which actually OU students get a chance to do in their first year of study. And what we can do is we're going to have a look at something called the sodium D-lines.

So let's have a look at the experiment over here. I've got a sodium lamp, and if it resembles something you can see before this orange glow, that's because it's absolutely correct. Old fashioned sodium streetlamps had exactly this orange kind of glow.

And then I've got what's called a spectroscope. It's basically two telescopes that from the eyepiece to basically the other end are giving me a view through to the lamp. And in the middle, I've got one of these diffraction gratings, just like we had before. 600 lines per millimetre.

And what I've done is I've set up this spectroscope so that it's looking at the first order light coming from the lamp and being diffracted through the diffraction grating. When I look through the eyepiece, what I can see is some bright colours. And if I actually cover up the experiment quite carefully, I can get a really beautiful view of what I'm seeing in this first order diffraction.

First of all, I can see a slightly blue colour, and the blue colour is a transition between two energy states of the atom. And then I can see a green colour and a yellow colour and a red colour.

And there's something very interesting about the lines. Have a look at the lines we're showing you on the screen now from down the eyepiece. What unusual about them?

That's right. There are two of them, but there's only one lamp. That's because sodium has a set of energy levels between which this transition is occurring. The electrons in the sodium atom are being excited by the electrical current and jumping up into the upper energy level and falling back down to the lower energy level.

But it's also true in quantum mechanics that electrons come, if you like, in two flavours-- two types of spin called spin up and spin down. And when the electron in the sodium atom is falling back down from this higher to the lower energy state, the spin of the electron is also important, and it leads to what we call a splitting of the energy levels and the sodium double D-lines.

And we can actually measure the exact difference in this energy by understanding that the photon, the energy of the light, given out as the electrons make these transitions, is very, very specific to the gap in the energy levels. So in a moment in the text, you're going to try and calculate this and look at the difference between those two energy levels with us giving you the numbers that you need to do those little calculations.

End transcript: Video 3 Sodium D-lines.

Download

Video 3 Sodium D-lines.

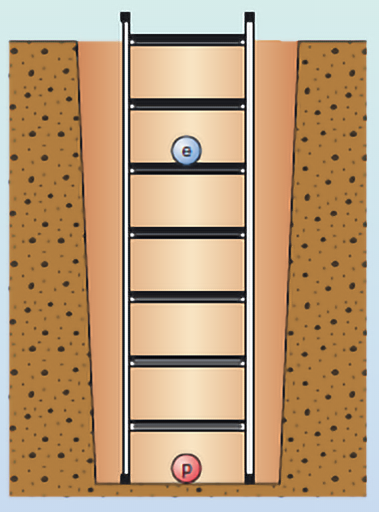
Video 3 introduced the concept of energy levels. These can be thought of as the rungs on a ladder (Figure 5).

Figure 5 The analogy of rungs on a ladder for energy levels.

Show description|Hide description

This image shows a ladder in a well. There are 7 rungs on the ladder with the top rung on the same level as the top of the well. There is a particle indicated as p in the bottom of this well, not on the lowest rung of the ladder. This p represents a proton. An electron, represented by the letter e, is shown on the 5th rung of the ladder, two rungs down from the top of the ladder.

Figure 5 The analogy of rungs on a ladder for energy levels.

Figure 5 represents the simplest atom, hydrogen. This atom has one electron ‘in orbit’ around the nucleus (labelled as the blue circle with the letter ‘e’). The nucleus of a hydrogen atom contains just one proton (labelled as the red circle with the letter ‘p’). The rungs on the ladder represent discrete and separate energy levels. In the ‘ground state’, the electron would be on the first rung of the ladder. This state is given the value n = 1. (Please note that this is not the same ‘n’ as in the diffraction equation). If you give the electron exactly the right amount of energy, it will then move up to the next rung of the ladder. Here it would be the second rung where n = 2. You can test your understanding of this in the next activity.

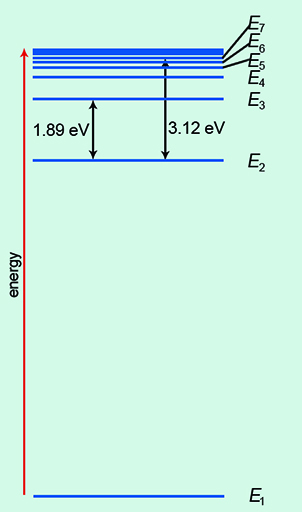
Of course, the real picture is more complicated than a simple ladder! In Figure 6, the ground state of energy is labelled E₁. As you move up the energy levels, they bunch closer together. The electrons can transition, or move, between each energy level. Indeed, there are numerous permutations.

Figure 6 Energy levels of a hydrogen atom.

Show description|Hide description

This is an image of the energy levels of a hydrogen atom. At the bottom of the image is a horizontal line indicated as E(1). A vertical arrow pointing upwards is labelled as increasing energy. 7 energy levels, E(2) to E(7) inclusive, are labelled with horizontal lines becoming increasingly more bunched up as the energy increases in the vertical direction. After E(7) subsequent energy levels are shown as a thick line. Two way arrows are drawn indicating energy transitions between energy levels; between E(2) and E(3) this is shown as 1.89 eV; between E(2) and E(7) this is shown as 3.12 eV.

Figure 6 Energy levels of a hydrogen atom.

You can see that the energy units of eV, or electronvolts, are used here. At this size in the quantum world, the usual unit of energy, the joule, is much too big.

Now complete this section on energy levels by doing Activity 6.

You will now look at quantum energy levels.