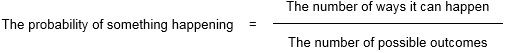10.1 Probability scales
In real life, things usually fall somewhere in between the two extremes of ‘will never happen’ and ‘will definitely happen’. However, some events are certain, while others are impossible: so for example, if you throw a standard dice, you’re certain to roll a number between 1 and 6, but it would be impossible to roll a 7.
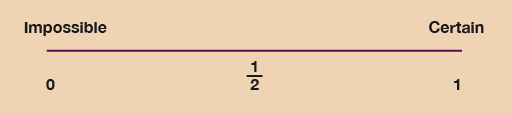
We can use a probability scale to measure how likely events are to occur:
- The probability of an impossible event (‘will never happen’) is 0.
- The probability of a certain event (‘will definitely happen’) is 1.
- All other events come between 0 and 1.
- Events with an even chance have a probability of one divided by two: , 50% or 0.5.
Now try the following activity, where you’ll need a ruler and a pencil. Remember to check your answers once you have completed the questions.
Activity 19: Looking at probability
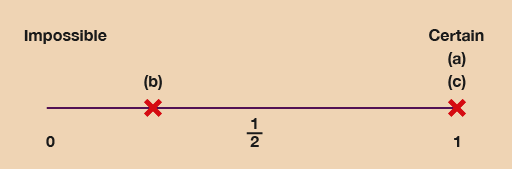
Use a ruler to draw your own probability scale. Mark on it ‘0’, ‘’ and ‘1’. Label 0 as ‘impossible’ and 1 as ‘certain’.
Then mark these statements on the probability scale with crosses and label them with their question letter:
- a.The probability that the sun will rise tomorrow.
- b.The probability that you will run the London Marathon next year.
- c.The probability of dying one day.
For some events it is not possible to give an exact probability of an outcome. In the example above, you had to use your knowledge to estimate the probability of you running in the London Marathon. A friend may give a different probability!
Weather forecasters predict the weather in a similar way, looking at the available data and historical trends (patterns) to give the most probable weather predictions. Weather forecasting is not exact, so the forecasters use their knowledge to present a weather report that has the highest probability of occuring. Bookmakers use similar skills to set odds, looking at past results, current form, etc.
For some events, however, it is possible to give an exact probability of an outcome. Mathematically we can say that:
Example: Types of probability
What is the possibility of tossing a coin and getting heads?
How many ways can it happen? One way: in this example, it’s either heads or it’s not.
How many possible outcomes are there? When we toss a coin there are two possible outcomes: heads or tails.
So the probability of tossing a coin and getting heads is one in two (that is, , 50% or 0.5).
What is the possibility of rolling a dice and getting a 6?
How many ways can it happen? One way: either it’s a 6 or it’s not.
How many possible outcomes are there? There are six numbers on a dice, so there are six possible outcomes.
So the probability of rolling a 6 on a dice is one in six.
What is the possibility of rolling a dice and getting an even number?
How many ways can it happen? There are three different ways we could roll an even number: the even numbers on a six-sided dice are 2, 4 and 6.
How many possible outcomes are there? There are six numbers on a dice, so there are six possible outcomes.
So the probability of rolling an even number on a die is three in six, which we can simplify to one in two (, 50% or 0.5).
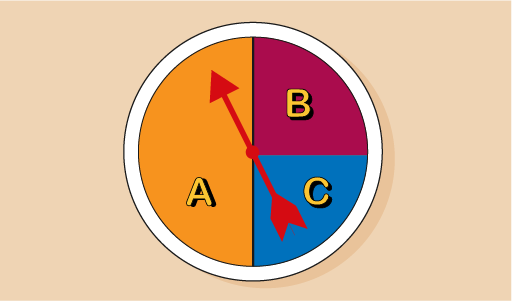
What is the probability of spinning an A?
In some situations the possibilities are not equally likely. Look at this spinner:
How many ways can it happen? One way: either you spin an A or not.
How many possible outcomes are there? The spinner has three numbers, but they are not all the same size – so the possibility of spinning an A is not one in three. We can see that section A of the spinner is twice as big as sections B and C, and takes up half of the spinner. So the probability of spinning an A is half, or one in two (, 50% or 0.5).
Activity 20: Calculating probability
- What is the probability of Huw rolling a dice and getting an odd number?
- Nancy is playing cards. What is the probability of her selecting:
- a.a red card from the deck of playing cards?
- b.an ace from the deck of cards?
- c.a heart from the deck?
- Harrison puts the letters that spell his name into a bag. What is the probability that he will pick out an R?
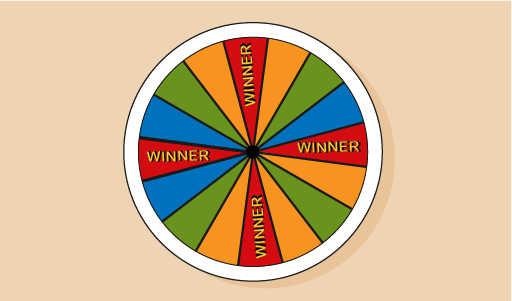
- David has designed a wheel of fortune to use in the school fete. What is the probability of spinning a win?
Answer
How many ways can it happen? There are three different ways that we could roll an odd number on a six-sided dice: a 1, 3 or 5.
How many possible outcomes are there? There are six numbers on a dice, so there are six possible outcomes.
So the probability of rolling an odd number on a dice is three in six, which we can simplify to one in two (, 50% or 0.5).
- The answers are as follows:
a.How many ways can it happen? There are 26 red cards in a deck of playing cards.
How many possible outcomes are there? There are 52 cards in a deck, so there are 52 possible outcomes.
So the probability of selecting a red card is 26 in 52, which we can simplify to one in two (, 50% or 0.5).
b.How many ways can it happen? There are four aces in a deck of playing cards.
How many possible outcomes are there? There are 52 cards in a deck, so there are 52 possible outcomes.
So the probability of selecting a red card is 4 in 52, which we can simplify to 1 in 13.
c.How many ways can it happen? There are 13 hearts in a deck of playing cards.
How many possible outcomes are there? There are 52 cards in a deck, so there are 52 possible outcomes.
So the probability of selecting a heart is 13 in 52, which we can simplify to one in four (, 25% or 0.25).
How many ways can it happen? There are two Rs in the name ‘Harrison’, so there are two ways that it can happen.
How many possible outcomes are there? There are eight letters in the name ‘Harrison’, so there are eight possible outcomes.
So the probability of selecting an R is two in eight, which we can simplify to one in four (, 25% or 0.25).
-
How many ways can it happen? There are four ‘winner’ sections, so there are four ways it can happen.
How many possible outcomes are there? There are 16 sections, so there are 16 sections that the spinner could land on.
So the probability of David spinning a win is 4 in 16, which we can simplify to one in four (, 25% or 0.25). The winning section covers a quarter of the spinner.
Summary
In this section you have:
- learned about the possibility of different events happening
- shown that some events are more likely to occur than others.