7.1 Solving ratio problems where the total is given
The best way for you to understand how to solve these problems is to look through the worked example in the video below.
Transcript
To understand how to solve ratio problems where the total is given, it's best to look through a worked example.
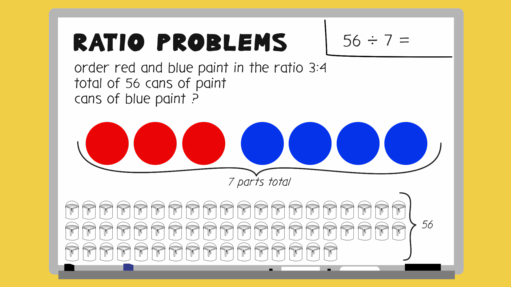
An art shop is ordering paint. They work out that they need to order red and blue paint in the ratio 3:4. They order a total of 56 cans of paint. How many of those cans are blue paint?
The first step to finding out, is to work out the total number of parts by adding together the parts of the ratio. If there are three parts red and four parts blue, that makes a total of seven parts altogether. Next, you need to work out what one part is worth. To do this, divide the total number of paint cans ordered, by the total number of parts. 56 divided by 7 equals 8. One part is worth eight cans.
Now, you know that one part of paint is 8 cans, you can work out what four parts are worth. 8 x 4 = 32. So the art shop needs to order 32 cans of blue paint.
Can you think of an extra check that you can carry out to confirm your answer? Well as you know what one part of paint is worth, you can also work out how many cans of red paint need to be ordered. 3 parts x 8 cans = 24 cans of red paint.
The total of red paint and blue paint should be 56. So you can check your answer by adding together the number of cans of each. 32 + 24 is indeed 56 cans.
So in summary, the steps for solving a ratio question like this are:
One. Add together the parts of the ratio. 3 + 4 = 7.
Two. Take the total amount given and divide by the sum of the ratio parts. 56 divided by 7 = 8.
Three. Finally, take the answer for step two, 8, and multiply by whichever part of the ratio you're interested in finding. 8 x 4 = 32.
Activity 13: Ratio problems where the total is given
Try solving these ratio problems:
To make mortar you need to mix soft sand and cement in the ratio 4:1. You need to make a total of 1500 g of mortar. How much soft sand will you need?
To make the mocktail ‘Sea Breeze’, you need to mix cranberry juice and grapefruit juice in the ratio 4:2. You want to make a total of 2700 ml of mocktail. How much grapefruit juice should you use?
Answer
Add the parts of the ratio:
4 + 1 = 5
Divide the total amount required by the sum of the parts of the ratio:
1500 g ÷ 5 = 300 g
Since soft sand is 4 parts, we do 300 g × 4 = 1200 g of soft sand.
Add the parts of the ratio:
4 + 2 = 6
Divide the total amount required by the sum of the parts of the ratio:
2700 ml ÷ 6 = 450 ml
Since grapefruit juice is 2 parts, we do 450 ml × 2 = 900 ml of grapefruit juice.
