1.1 Expressing a remainder as a decimal

To split a prize of £125 between 5 friends you would do this calculation:

• £125 ÷ 5 and get the answer £25.

This is a convenient, exact amount of money. However, often when you perform calculations, especially those involving division, you do not always get an answer that is suitable for the question.

For example, if there were 4 friends who shared the same prize we would do the calculation £125 ÷ 4 and get the answer £31 remainder £1. If we did the same calculation on a calculator you would get the answer £31.25, the remainder has been converted into a decimal. Let’s look at how to express the remainder as a decimal.

You can write one hundred and twenty five pounds in two different ways: £125 or £125.00. Both ways show the same amount but the second way allows you to continue the calculation and express it as a decimal.

Figure 2 Expressed as a decimal: 125 ÷ 4

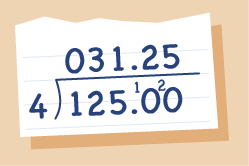
We can use the same principal with any whole number, adding as many zeros after the decimal point as required. Look at the following example.

A teacher wants to share 35 kg of clay between 8 groups of students. How much clay will each group get?

Figure 3 Expressed as a decimal: 35 ÷ 8

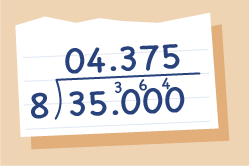
You can see that each group would get 4.375 kg of clay.