11.2 Formulas in practice
You will already have come across and used formulas in your everyday life. For example, if you are trying to work out the cost of a new carpet you will have used the formula:
area = length × width
to calculate how much carpet you would need.
Often division in a formula is shown as one number over another, for example:
6 ÷ 3 would be shown as
Let’s look at division in a formula:
A lorry driver travels 120 miles in 3 hours. What was the average speed during the journey?
Note: As the lorry driver was unlikely to have travelled at a constant speed for 120 miles we say we are calculating the average speed as this will give us the typical overall speed.
speed =
speed = 40 miles per hour
Sometimes we use letters to represent the different elements used in a formula, e.g. the formula above might be shown as:
s =
where:
‘s’ = speed in mph
‘d’ = distance in miles
‘t’ = time in hours
If you are trying to work out the time to cook a fresh chicken you may have used the formula:
Time (minutes) = 15 + × 25 where ‘w’ is the weight of the chicken in grams.
For example, if you wanted to cook a chicken that weighs 2500 g you would do:
Time (minutes) = 15 + × 25
Remembering to use BIDMAS you would then get:
Time (minutes) = 15 + 5 × 25
= 15 + 125
= 140 minutes
Let’s look at another worked example before you try some on your own.
Example: Gas bill formula
The owner of a guesthouse receives a gas bill. It has been calculated using the formula:
Cost of gas (£) =
Note: 8d means you do 8 × d.
Where d = number of days and u = number of units used, if she used 3500 units of gas in 90 days, how much is the bill?
In this example, d = 90 and u = 3500 so you do:
Cost of gas (£) =
=
=
= £42.20
Activity 31: Using formulas
Fuel consumption in Europe is calculated in litres per 100 kilometres. A formula to approximate converting from miles per gallon to litres per 100 kilometres is:
L =
where L = number of litres per 100 kilometres and M = number of miles per gallon.
A car travels 40 miles per gallon. What is this in litres per kilometres?
Answer
- L = and in this case M = 40
- L =
- L = 7 litres per 100 kilometres
Using the formula I = where:
I = interest
P = principal amount of loan
R = interest rate
T = time in years
calculate how much interest is due on a loan of £5000 taken over 3 years at an interest rate of 5.5%.
Answer
I =
In this case P = £5000, R = 5.5% and T = 3 years.
I =
I =
I = 825
So the interest paid would be £825.
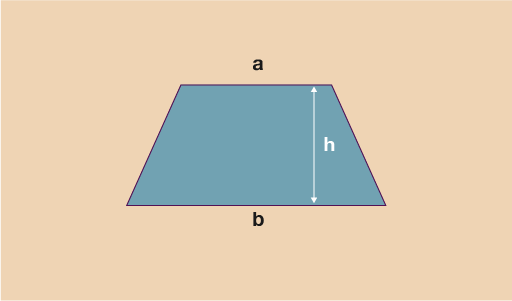
- The area of a trapezium can be calculated using the formula:
A =
Find the area of trapeziums where:
- i.a = 5 cm, b = 9 cm and h = 7 cm
- ii.a = 35 mm, b = 40 mm and h = 10 cm
Answer
A =
i.A =
A =
A =
A = 49 cm2
ii.In this question you must convert the units so that they are all the same. The units that you select will be the units that your answer will be given in, e.g. if you convert to mm your answer will be in mm2 but if you convert to cm your answer will be in cm2.
A =
Method 1 – converting to mm
Convert h measurement to mm:
10 × 10 = 100 mm
A =
A =
A =
A = 3750 mm2
Method 2 – converting to cm
Convert a and b measurements to cm:
a = 35 ÷ 10 = 3.5 cm
b = 40 ÷ 10 = 4 cm
A =
A =
A =
A = 37.5 cm2
Note: it is a good idea to show all the stages of the calculation to help you keep track of your workings.
A company uses the following formula to work out the total cost to the customer of hiring a bouncy castle:
T = hc + (0.45d) + 15
where:
T = total
h = number of days hire
c = cost of castle per day
d = delivery distance in miles.
Stuart lives 12 miles away and would like to hire a Supersonic Castle for 2 days. How much will it cost?
Answer
T = hc + (0.45d) + 15
In this case h = 2, c = £42, and d = 12, so:
T = 2 × 42 + (0.45 × 12) + 15
T = 84 + 5.4 + 15
T = 104.4
The total cost of hire would be £104.40.
Now that you have learned all the skills that relate to the number section of this course, there is just one final thing you need to be able to do before you will be ready to complete the end-of-session quiz for numbers.
You are now proficient at carrying out lots of different calculations including working out fractions and percentages of numbers, using ratio in different contexts and using formulas.
It is fantastic that you can now do all these things, but how do you check if an answer is correct? One way you can check would be to approximate an answer to the calculation (as you did in Section 3.2). Another way to check an answer is to use the inverse (opposite) operation.
Summary
In this section you have:
- learned about, and practised using BIDMAS – the order in which operations must be carried out
- seen examples of formulas used in everyday life and practised using formulas to solve a problem.