4 How many will fit?
You may need to work out how many tiles to buy to tile an area of wall or how many tins you can pack in a box. We will use the example below to illustrate.
Example 1: Tiling a wall
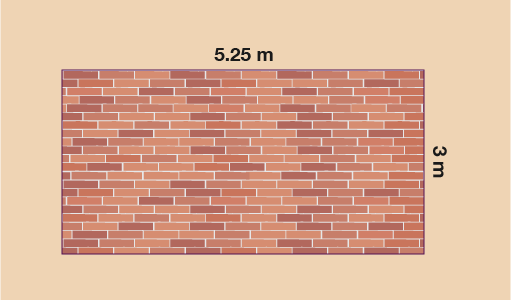
You are going to buy tiles measuring 0.75 m by 0.75 m to tile this area of wall:
How many tiles do you need to buy?
The easiest way to tackle a question such as this is to work out how many tiles will fit across the wall and how many will fit down the wall. You can then work out how many you need altogether.
The length across the wall is 5.25 m so we can divide by the length of the tile to work out how many will fit:
5.25 ÷ 0.75 = 7 tiles across
You may have preferred to convert the measurements into centimetres to avoid dividing by a decimal:
1 m = 100 cm, so
5.25 × 100 = 525 cm
0.75 × 100 = 75 cm
525 ÷ 75 = 7 tiles (you can see that the number of tiles is the same.)
Down the wall the measurement is 3 m, so down the wall you will fit:
3 ÷ 0.75 = 4 tiles (you may have converted to cm again and done 300 ÷ 75 = 4 tiles)
If 7 tiles will fit across the wall and 4 will fit down then altogether you will need:
7 × 4 = 28 tiles.
Example 2: Packing calculations
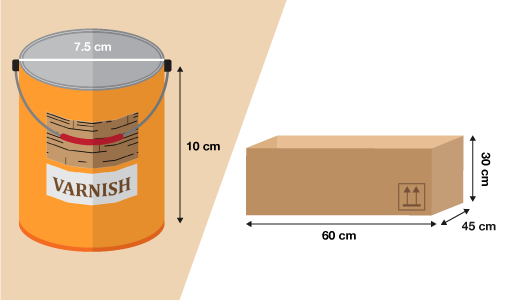
A shop is packing tins of varnish into boxes for delivery. The tins are cylindrical with a diameter of 7.5 cm and a height of 10 cm. The packing box is 60 cm long, 45 cm wide and 30 cm high.
How many tins can be packed into each box?
The easiest way to tackle this type of question is to work out how many tins you can fit in a single layer first and then to work out how many layers you can have. To work out how many tins will fit in a single layer use the same method you used above for working out how many tiles would fit.
The box is 60 cm long and tins are 7.5 cm wide:
- 60 ÷ 7.5 = 8 so 8 tins will fit across the box.
Hint: make sure you are working with the diameter and not the radius of the cylinder.
The box is 45 cm wide:
- 45 ÷ 7.5 = 6
- so 6 tins would fit.
This would give 6 rows of 8 tins:
- 8 × 6 = 48
- so 48 tins would fit in 1 layer.
Next you need to work out how many layers you could fit. The tins are 10 cm high and the box is 30 cm high:
30 ÷ 10 = 3
so the tins can be stacked 3 high:
- 3 × 48 = 144
The box would hold 144 tins.
Now try the following questions. Please carry out the calculations without a calculator. You can double check with a calculator if needed and remember to check your answers against ours.
Activity 8: How many will fit?
You want to re-carpet your floor using carpet tiles. Your floor measures 4.5 m by 6 m. The tiles you like measure 0.5 m by 0.5 m and cost £1.89 per tile.
a.How many tiles will you need to buy?
b.How much will they cost altogether?
Answer
a.You need to work out how many tiles will fit across the length of the floor and across the width of the floor.
Length
The floor is 6 m long. Each tile is 0.5 m by 0.5 m so to work out how many will fit do:
6 ÷ 0.5 = 12 tiles
You could also convert to centimetres:
6 m = 6 × 100 = 600 cm
0.5 m = 0.5 × 100 = 50 cm
600 ÷ 50 = 12 tiles
Width
The floor is 4.5 m wide. Each tile is 0.5 m by 0.5 m so to work out how many will fit do:
4.5 ÷ 0.5 = 9 tiles
You could also convert to centimetres:
4.5 m = 4.5 × 100 = 450 cm
0.5 m = 0.5 × 100 = 50 cm
450 ÷ 50 = 9 tiles
So altogether you need:
12 × 9 = 108 tiles
b.Each tile costs £1.89 and you need 108 tiles so the total cost of the tiles will be:
1.89 × 108 = £204.12
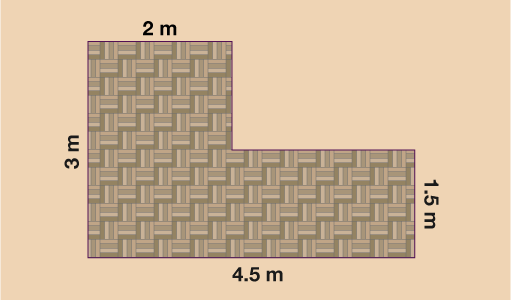
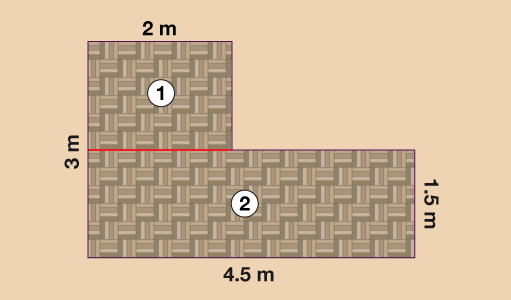
How many 25 cm square tiles would you need to tile the floor area below?
Answer
You need to split the floor up into 2 rectangles. You could do this in a couple of different ways.
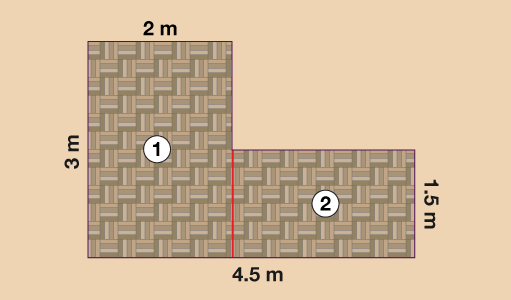
First method for splitting the floor as follows:
Rectangle 1
Rectangle ① is 3 m by 2 m. Convert the dimensions into centimetres:
3 m × 100 = 300 cm
2 m × 100 = 200 cm
The tiles are 25 cm square (25 cm by 25 cm) so you will need:
- 300 ÷ 25 = 12
- 200 ÷ 25 = 8
- so for this part of the floor you will need:
- 12 × 8 = 96 tiles.
Rectangle 2
Rectangle ② is 1.5 m by 2.5 m (4.5 m − 2 m = 2.5 m). Convert the dimensions into centimetres:
1.5 m × 100 = 150 cm
2.5 m × 100 = 250 cm
The tiles are 25 cm square (25 cm by 25 cm) so you will need:
- 150 ÷ 25 = 6
- 250 ÷ 25 = 10
- so for this part of the floor you will need:
- 6 × 10 = 60 tiles.
So altogether you will need:
60 + 96 = 156 tiles to tile the floor.
You may have split the floor area up differently.
Second method for splitting the floor as follows:
Rectangle 1
Here rectangle ① is 1.5 m by 2 m (3 − 1.5 m = 2 m). Convert the dimensions into centimetres:
- 1.5 m × 100 = 150 cm
- 2 m × 100 = 200 cm
The tiles are 25 cm square (25 cm by 25 cm) so you will need:
- 150 ÷ 25 = 6
- 200 ÷ 25 = 8
- so for this part of the floor you will need:
- 6 × 8 = 48 tiles
Rectangle 2
Here rectangle ② is 1.5 m by 4.5 m. Convert the dimensions into centimetres:
1.5 m × 100 = 150 cm
4.5 m × 100 = 450 cm
The tiles are 25 cm square (25 cm by 25 cm) so you will need:
- 150 ÷ 25 = 6
- 450 ÷ 25 = 18
- so for this part of the floor you will need:
- 6 × 18 = 108 tiles
So altogether you will need:
48 + 108 = 156 tiles to tile the floor.
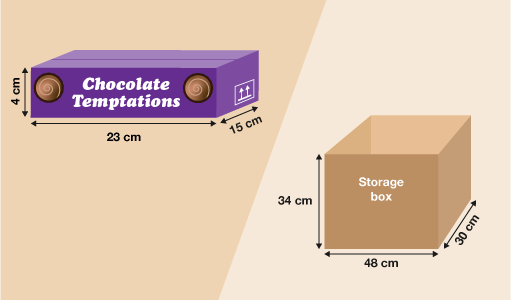
You are packing boxes of chocolates. Each chocolate box measures 23 cm long by 15 cm wide by 4 cm high and you are packing them into a storage box measuring 48 cm long by 30 cm wide by 34 cm high.
What is the maximum number of chocolate boxes that can be packed in one storage box?
Hint: The chocolate boxes need to be packed flat (horizontally) but you may want to try turning the chocolate box around.
Answer
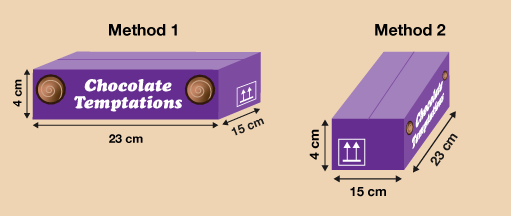
The chocolate boxes need to be packed flat (horizontally). However, the boxes could be packed in 2 different ways:
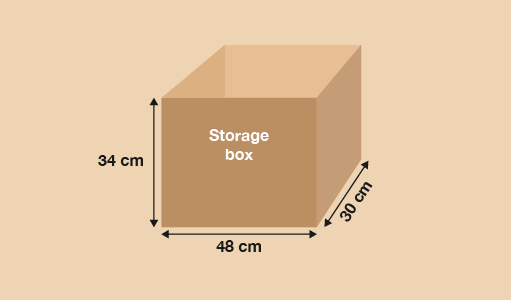
Remember the dimensions of the storage box are as follows:
Method 1
If you packed the chocolate boxes this way the storage box is 48 cm long and the chocolate boxes are 23 cm long so the calculation would be:
48 ÷ 23 = 2.1 (rounded to one d.p.)
so only 2 chocolate boxes will fit.
The storage box is 30 cm wide and the chocolate boxes are 15 cm wide so:
30 ÷ 15 = 2
- so 2 chocolate boxes would fit.
This would give 2 rows of 2 chocolate boxes:
2 × 2 = 4
so 4 chocolate boxes would fit in 1 layer.
Next you need to work out how many layers you could fit. The storage box is 34 cm high and the chocolate boxes are 4 cm high:
34 ÷ 4 = 8.5
so 8 chocolate boxes will fit.
The chocolate boxes can be stacked 8 high so:
8 × 4 = 32
If using Method 1 the storage box would hold 32 chocolate boxes.
Method 2
If you packed the chocolate boxes this way the calculation would be as follows:
48 ÷ 15 = 3.2 so 3 boxes will fit
30 ÷ 23 = 1.3 (rounded to one d.p.) so only 1 will fit
In one layer, you could fit 3 × 1 = 3 chocolate boxes.
Next you need to work out how many layers you could fit. The storage box is 34 cm high and the chocolate boxes are 4 cm high:
34 ÷ 4 = 8.5
so only 8 chocolate boxes will fit.
The chocolate boxes can be stacked 8 high:
8 × 3 = 24
If using Method 2 the storage box would hold 24 chocolate boxes.
Therefore, the maximum number of chocolate boxes that could fit into the storage box is 32 and you would have to pack them the first way (Method 1) to achieve this.
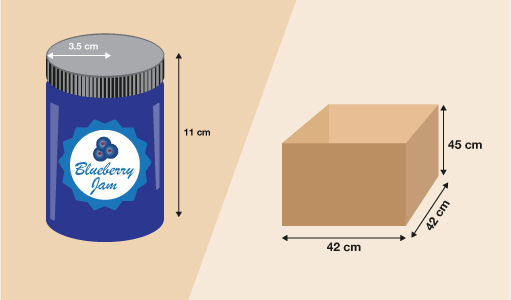
A factory producing jars of jam packs the jars into boxes that measure 42 cm long, 42 cm wide and 45 cm high. The jars of jam have a radius of 3.5 cm and a height of 11 cm.
How many jars of jam can be packed into a box? The jars must be packed upright.
Answer
First you need to calculate the diameter (width) of the jars. The radius of the jars is 3.5 cm:
3.5 × 2 = 7
so the diameter of the jars is 7 cm.
The box is 42 cm wide and jars are 7 cm wide:
42 ÷ 7 = 6
so 6 jars will fit across the box.
The length of the box is also 42 cm so you know that there will be 6 rows of 6 jars on the bottom layer.
6 × 6 = 36
so 36 jars will fit in 1 layer.
Next you need to work out how many layers you could fit. The jars are 11 cm high, and the box is 45 cm high:
45 ÷ 11 = 4.09 to two d.p.
so the tins can be stacked 4 high.
4 × 36 = 144
So 144 jars of jam would fit in each box.
The final part of his section will look at scale drawings and plans. It will require your previous knowledge of ratio as scale drawings are really just another application of ratio. The good news then, is that you already know how to do it!
Summary
In this section you have:
- learned to calculate how many smaller shapes or items will fit into larger areas or spaces.