4.4 Correlation, causation and coincidence
Graphs are a great tool for presenting complicated results: they can help communicate the relationship between two or more variables.
Correlation
A striking example of this is the recognition of a correlation between smokers and lung cancer patients. Lung cancer used to be a rare disease, with only 1% of autopsies performed by the Institute of Pathology of the University of Dresden in 1878 showing malignant lung tumours. Unfortunately, lung cancer did not remain rare and, over the following 50 years, this figure rose to more than 14%.
Causation
A particularly observant scientist, Franz Müller from Cologne Hospital, published a study in 1939, identifying the correlation between tobacco smoke and lung cancer. The study compared 86 lung cancer cases and a similar number of cancer-free controls, showing that the people who smoked were far more likely to suffer lung cancer.
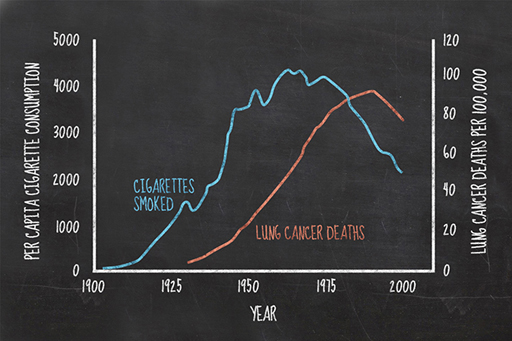
However, while a correlation between two sets of observations or measurements can point to a causal relationship between them, correlation does not always imply causation. This was part of the basis for the long running debate about smoking and lung cancer, but it was some decades later before this link was accepted following the emergence of scientific evidence for the cause.
Coincidence
Consider this odd correlation between worldwide launches of non-commercial space missions and the number of sociology doctorates awarded in the USA. The graph shows how both of these variables rise and fall together, as if connected in some way. You might wonder if the sociology graduates work on the space missions? However, this is not the case, with sociology doctorates usually working in the field that they are actually trained in and not turning their hands to physics or space engineering. This correlation, as real as it is, is a coincidence. It is also not a freak occurrence; a quick internet search of ‘spurious correlations’ will bring up a whole host of correlations that are purely coincidental.
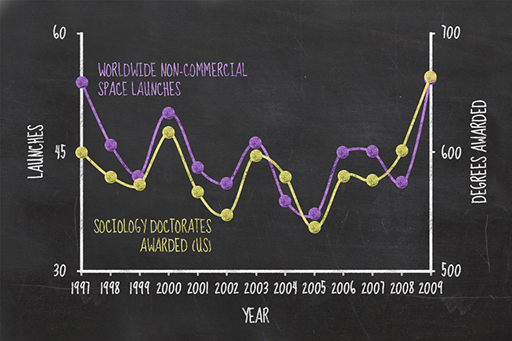
The role of a scientist is to critically assess correlations encountered in their results. There are several criteria scientists use to test the validity of correlations and their significance. The detail is beyond the scope of this course, but they are a crucial science skill. Ways of testing correlations include the goodness of fit, in other words, working out how good the correlation is, and whether it can be reproduced and examined further.
What about the apparent correlation in the graph of space missions and sociology graduates? A scientist might ask why the graph is only plotted between the years 1997 and 2009, since both space missions and sociology graduates were around before and after those dates – did the person plotting the data avoid those earlier and later dates because the correlation breaks down?
Despite the precaution such as goodness of fit and reproducibility, sometimes scientists get it wrong and over interpret a correlation or apply causal mechanisms to coincidences. Can you think of any examples where this has been the case?
