4.6 Average densities
If a planet is composed of different layers each having different densities, then the density of the planet as a whole will be averaged over the various layers. To give the average density of a planet, the total mass is divided by the total volume:
In this way you can measure the average densities of some planets orbiting around other stars even though you can’t see them, as you will learn in future weeks. If a planet has the density of rock, it is probably composed of rock. If it has the density of hydrogen gas, that is probably what it is composed of. Iron is the densest material you might expect to find in a planet, while a mixture of hydrogen gas with a small amount of helium is the least dense material you might expect to find.
However, you must be careful about conclusions such as those above. The average density of a planet might not tell you what the planet is made of. It is possible to imagine a planet with an iron core surrounded by hydrogen/helium gas, which averages out to exactly the density of rock. In this case, the conclusion that the planet is composed of rock would be completely wrong. From the average density, it is impossible to be sure exactly how much of each layer is present.
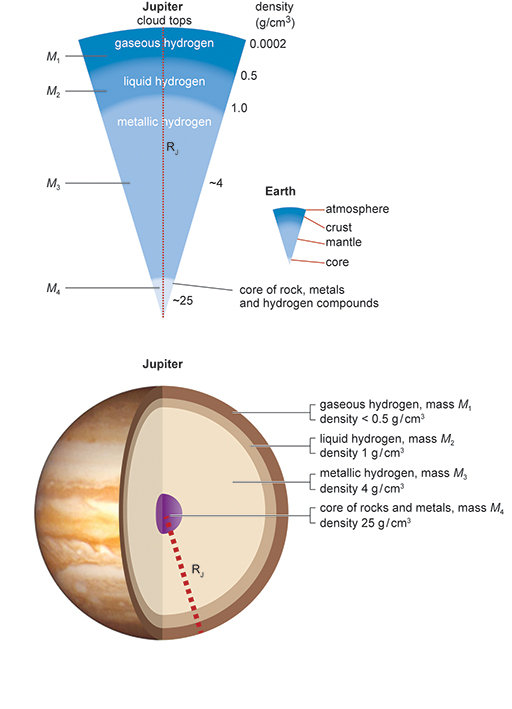
As you go down to deeper layers of the planet Jupiter, you can see how much the density increases (Figure 12). Density is often expressed in units of grams per cubic centimetre (g/cm3), so the numbers in Figure 12 say how many grams of material are contained in each cubic centimetre. Near the core the density is expected to be around 25 g/cm3, which means that each centimetre cube contains material that has a mass of 25 grams. As a comparison, the density of liquid water on Earth is 1 g/cm3.
Activity 3 The density of a layered planet
In this activity you will calculate the density of a layered planet, in this case, Jupiter, which is shown in Figure 12.
- On a piece of paper, write down a sum giving the total mass M of Jupiter in terms of the masses of its four layers, M1, M2, M3 and M4.
Answer
- Write down an expression for the volume of Jupiter in terms of its radius, RJ.
- Referring to your answers to Part 1 and Part 2, write down an expression for the density of Jupiter in terms of M and RJ.
Answer
- Use your answer to Part 3 and the data listed below to calculate the average density of Jupiter.
Total mass of Jupiter: 1.898 × 1030 g
Average radius of Jupiter: 6.991 × 10 9 cm
Answer
We use the expression for density found in Part 3 and substitute the numbers for the mass and average radius into it. This gives
Jupiter’s average density is 1.3 g/cm3, which means that each centimetre cube of material has a mass of 1.3 grams on average – a little more than the density of water on Earth.
Note that the answer to a calculation like this should be rounded to convey how precisely the measurements used in the calculation are known. There are rules for this, but in this course it is generally suitable to round to two or three digits.
Maths help
The following OpenLearn resources may help with the maths in this section. Open the link in a new tab or window by holding down Ctrl (or Cmd on a Mac) when you click on the link. Remember to return here when you have finished.