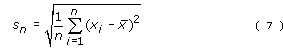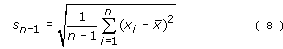3 Samples and populations
It is no accident that the examples used to illustrate the statistics for repeated measurements of individual quantities were drawn from chemistry and physics. Experiments involving repeated measurements of some quantity are typical of the physical sciences. There are, however, many other types of scientific work in which a typical procedure is to collect data by measuring or counting the members of a sub-set of things which form part of a larger group, and the previous section contained several examples. In this type of work, the sub-set of members that are measured or counted is called the sample and the larger group is called a population. Although often employed in the context of biology to describe a group of organisms that might breed with one another, the term 'population' is used much more widely in statistics to mean an aggregate of things or events. Examples of statistical populations could include all the sand grains on a beach, all the leaves on a single tree, all the people in England with blood group AB, or all the visits made to the Science Museum in March.
It is generally the case that the members of any one population display some variability; for instance, not all the leaves on an oak tree will be exactly the same size. Furthermore, different populations often overlap with respect to whatever we might be measuring or counting. But despite this variability and overlap, what scientists often want to know is whether there seem to be systematic differences between the populations. Indeed, only if there do seem to be such differences do they accept that they really are dealing with more than one population. Failure to find evidence of systematic differences between the leaves of oak trees growing on sandy soil and those of oak trees growing on clay soil would suggest that the leaves (and trees) were members of the same population, or in other words that soil conditions have no overall effect on the leaves of oak trees. In order to make use of the statistical techniques used in looking for systematic differences between populations it is necessary to be able to summarize the data that have been collected. You saw that for repeated measurements data sets could be summarized by quoting just two quantities: the mean and the standard deviation. This is also true for samples drawn from populations, but the mean and the standard deviation take on slightly different meanings in this context.
It is normally the case that data cannot be collected on all members of a population. It would indeed be impractical to attempt to measure every leaf on an oak tree! By the same token, it is usually impossible to know the true mean of some quantity for a whole population. This ‘true mean’ (also known as the ‘population mean’) is given the symbol μ (the Greek letter ‘mew’), with the understanding that this quantity is generally not only unknown but unknowable. What we can easily calculate, however, is the mean of the quantity as measured for a sample drawn from the population. This is given the symbol ![]() and calculated using Equation 3 [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] , exactly as you did before. Provided the sample is unbiased,
and calculated using Equation 3 [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] , exactly as you did before. Provided the sample is unbiased, ![]() is the best estimate of μ that we can obtain.
is the best estimate of μ that we can obtain.
As with the mean, the true standard deviation of a population can usually never be known with certainty. Again, the best estimate we can obtain must come from the distribution of values in a sample drawn from the population. However, this time it isn’t appropriate to use the formula for the standard deviation of repeated measurements of one quantity which was:
Instead a slightly different formula is used, namely:
sn–1 is often called the ‘sample standard deviation’ because it is calculated from data taken for a sample of the population.
The value determined for sn–1 provides the best estimate of the standard deviation of the population. It will not have escaped your notice that the only difference between the two formulae is that in Equation 8 you divide by (n–1), whereas in Equation 7 you divide by n. This means that sn–1 must always be larger than sn (because we are dividing by a smaller number). This allows for the possibility that within the whole population there may be a few extremely high or low values of the measured quantity which will not necessarily be picked up in a sample drawn from that population.
sn–1 is also often called the ‘estimated standard deviation of the population’ because, provided the sample is chosen without bias, it is the best estimate that can be made of the true standard deviation of the population.
Check that you can use your calculator to determine the sample standard deviation sn–1 for a set of data by doing Activity 3.
Activity 3 Using a calculator to calculate the sample standard deviation
Follow these five steps to calculate the sample standard deviation, using these numbers:
8, 6, 9, 12, 10
The first four steps are the same as before, only Step 5 will be different.
Step 1
Put the calculator into statistical mode.
Step 2
Input all the data.
Step 3
If your calculator can tell you the number of items of data, check that it gives the answer ‘5’ here.
Step 4
When you know you have the data correctly stored, display the mean; you should get the answer ‘9’ here.
Step 5
Now find out how to display the sample standard deviation. The appropriate button will probably be marked σn–1 or sn–1. You should get the answer ‘2.2’ here (to one decimal place). Don’t use the σn or sn button by mistake!
While this example is useful to familiarize yourself with the process, it doesn’t represent a realistic scenario, not least because the hypothetical data set is so small. Because the aim is to estimate the mean and standard deviation for a whole population by carrying out measurements just on a sample, it is important to ensure that the sample is representative of the population as a whole and that usually requires it not only to be chosen without bias, but also to be reasonably large. In Activity 4, the sample consists of 20 plants.
Activity 4 Flowers: finding the mean
Suppose that the number of flowers were counted on 20 orchid plants in a colony, and that the results were:
8; 8; 4; 8; 8; 7; 9; 7; 7; 5; 9; 10; 6; 9; 7; 4; 8; 5; 11; 5.
From these data, estimate to 3 significant figures the mean number, μ, of flowers per plant in the colony and the population standard deviation. You may if you wish construct a table similar to Table 2 in Week 7, but it will be much quicker simply to use your calculator.
Answer
The best estimate that can be made from these data of the mean number, μ, of flowers per plant in the colony is the mean of the sample, ![]() . In this case:
. In this case:
![]() = 7.25 flowers
= 7.25 flowers
{Note that it is normal practice to quote means and medians in this way, even for quantities, such as numbers of flowers, which cannot really be fractional!}
The best estimate that can be made of the population standard deviation is the sample standard deviation sn–1. In this case:
sn–1 = 1.94 flowers
That was the final activity of the week and the course. You now have a chance to practice your new knowledge and skills in the final quiz of the course.