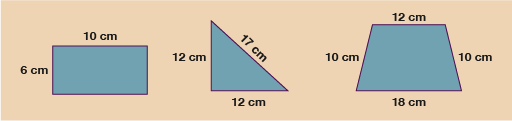
1.1 Perimeter of simple shapes
In order to work out the perimeter of the shapes above, all you need to do is simply add up the total length of each of the sides.
- Rectangle: 10 + 10 + 6 + 6 = 32 cm.
- Triangle: 12 + 12 + 17 = 41 cm.
- Trapezium: 10 + 12 + 10 + 18 = 50 cm.
When you give your answer, make sure you write the units in cm, m, km etc. One other important thing to note is that before you work out the perimeter of any shape, you must make sure all the measurements are given in the same units. If, for example, two lengths are given in cm and one is given in mm, you must convert them all to the same unit before you work out the total. It doesn’t usually matter which measurement you choose to convert but it’s wise to check the question first because sometimes you might be asked to give your answer in a specific unit.
Activity 1: Finding the perimeter
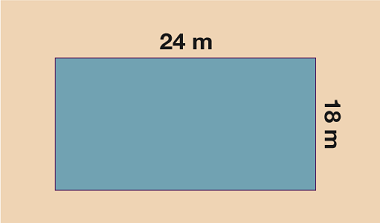
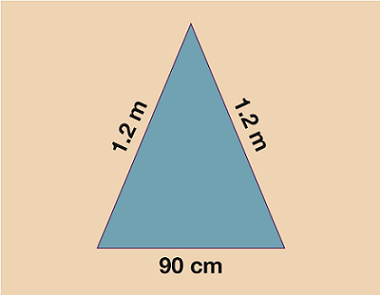
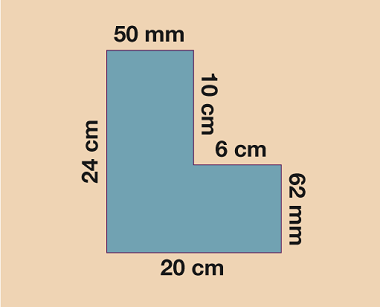
Work out the perimeters of each of the shapes below.
Remember to give units in your answer and to check that all measurements are in the same units before you begin to add.
Answer
- 24 + 18 + 24 + 18 = 84 m.
- If you worked in cm:
1.2 m = 120 cm.
Therefore, the perimeter is 120 + 120 + 90 = 330 cm.
If you worked in m:
90 cm = 0.9 m.
Therefore, the perimeter is 0.9 + 1.2 + 1.2 = 3.3 m.
- 50 mm = 5 cm, 62 mm = 6.2 cm.
Therefore, the perimeter is 24 + 5 + 10 + 6 + 6.2 + 20 = 71.2 cm.
Hopefully, you found working out the perimeters of these shapes fairly straightforward.
The next step on from shapes like the ones you have just worked with, is finding the perimeter of shapes where not all the lengths are given to you. In shapes such as a rectangle or regular shapes like squares (where all sides are the same length) this is a simple process. However, in a shape where the sides are not the same as each other, you have a little more work to do.