2.3 Area of a circle
The formula to find the area of a circle is similar to the one you have already used to find the circumference.
- Area of a circle = pi × radius2
- A = πr2
Hint: Remember that when you square a number you simply multiply it by itself, radius2 is therefore simply radius × radius.
Let’s look at an example.
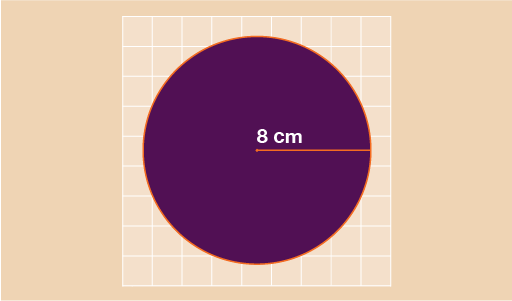
In the circle above you can see that the radius is 8 cm. To find the area of the circle we use:
- A = π r2
- A = 3.142 × 8 × 8
- A = 201.088 cm2
Before you try some on your own, let’s take a look at one further example.
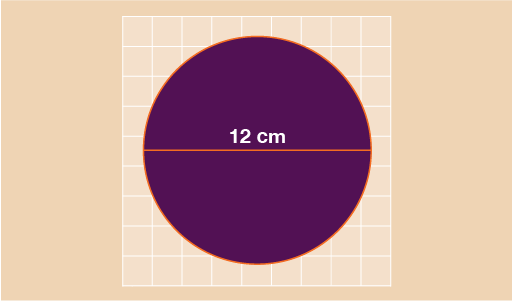
This circle has a diameter of 12 cm. In order to find the area, you first need to find the radius. Remember that the radius is simply half of the diameter and so in this example radius = 12 ÷ 2 = 6 cm.
We can now use:
- A = πr2
- A = 3.142 × 6 × 6
- A = 113.112 cm2
Try a couple of examples for yourself before moving on to the next part of this section.
Activity 6: Finding the area of a circle
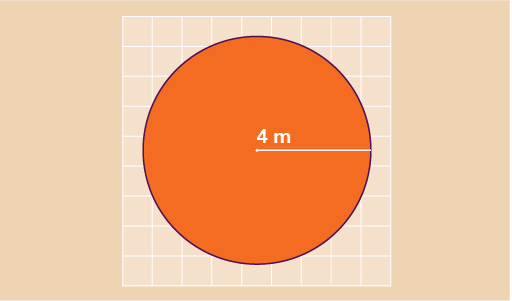
- Find the area of the circle shown below. Give your answer to one decimal place.
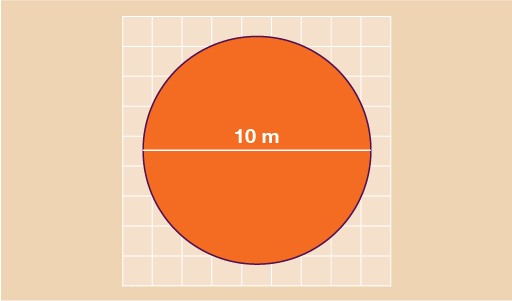
- You are designing a mural for a local school and need to decide how much paint you need. The main part of the mural is a circle with a diameter of 10 m as shown below. Each tin of paint will cover an area of 5 m2. You will need to use two coats of paint. How many tins of paint should you buy?
Answer
- Using the formula: A = πr2
- A = 3.142 × 4 × 4
- A = 50.272 m2
- A = 50.3 m2 to 1 d. p.
- You need to find the area of the circle first. Since the diameter of the circle is 10 m, the radius is 10 m ÷ 2 = 5 m.
Using the formula: A = πr2
- A = 3.142 × 5 × 5
- A = 78.55 m2
So the area of the circle you need to paint is 78.55 m2
Since you need to give 2 coats of paint, you need to double this number:
- 78.55 × 2 = 157.1 m2
You now need to work out how many tins of paint you need. As one tin of paint covers 5 m2 you need to do:
- 157.1 ÷ 5 = 31.42 tins
Since you must buy whole tins of paint, you will need to buy 32 tins.
You have now learned all you need to know about finding the area of shapes! The last part of this section is on finding the volume of solid shapes – or three-dimensional (3D) shapes .
Summary
In this section you have learned:
- that area is the space inside a two-dimensional (2D) shape or space
- how to find the area of rectangles, triangles, trapeziums and compound shapes
- how to use the formula to find the area of a circle.