4 Scale drawings and plans
Given that you already have the knowledge you need around measures and ratios, scale drawings are simply just another application of these skills.
Transcript
You have already developed skills in using measures and ratio. Scale drawings are just another application of this knowledge. So the good news is you already know how to do it. With this topic, it's best to dive straight in with an example.
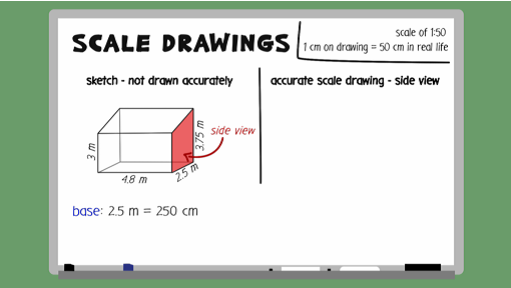
Ahmed is going to make some home improvements. He wants to build a conservatory. Here is Ahmed's sketch of the conservatory. He uses a scale of 1 to 50. You need to draw an accurate scale drawing of the side view, using Ahmed's scale.
The scale, or ratio, we are working with is 1 to 50. This means that every 1 centimetre on the scale drawing represents 50 centimetres in real life. To be able to work out the measurements required on the scale drawing, you must first convert all measurements to centimetres. The base is 2.5 metres, which equals 250 centimetres. The shortest vertical side is 3 metres, which equals 300 centimetres. The longest vertical side is 3.75 metres, which equals 375 centimetres.
Now to work out the length of each side on the scale drawing. Since 1 centimetre on the drawing is 50 centimetres in real life, you need to divide the real-life measurement by 50 in order to work out the length required on the drawing. The base, 250, divided by 50, equals 5 centimetres. The shortest vertical side, 300, divided by 50, equals 6 centimetres. The longest vertical side, 375, divided by 50, equals 7.5 centimetres. To get the diagonal length, you simply join the tops of the two other sides together. Now work through the next few examples.
If you are given the scale drawing and asked to work out the real-life size, rather than dividing by the scale, you multiply by it. Take a look at the example below.
Example: Calculating scale
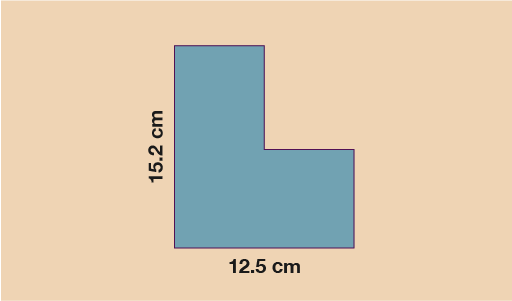
A scale drawing has been drawn below of a shed that a garden planner wants to build. The scale used for the drawing is 1:20. The area that the shed will be built on is a rectangle which measures 3.1 m by 2.8 m.
Will the building fit into the space allocated?
Method
Since 1 cm on the diagram represents 20 cm in real life, you do:
Horizontal length: 12.5 × 20 = 250 cm = 2.5 m
Vertical length: 15.2 × 20 = 304 cm = 3.04 m
Since both lengths for the shed are shorter than the lengths given for the area of land, you know the shed will fit.
Now have a go at an example for yourself.
Activity 8: Finding the length of a slope
For this question you will need a pen or pencil, paper and a ruler.
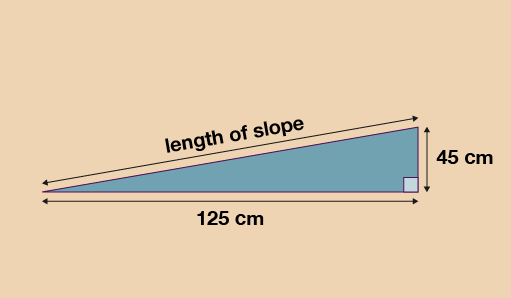
Jane has a raised vegetable patch. She plans to build a slope leading up to the vegetable patch. Jane will cover the slope with grass turf.
She draws this sketch of the cross section of the slope.
Jane will use a scale diagram to work out the length of the slope. She wants to use a scale of 1:10.
Draw a scale diagram of the slope for Jane. Use it to find the length of the slope.
Answer
Base of patch = 125 ÷ 10 = 12.5 cm
Height of patch = 45 ÷ 10 = 4.5 cm
The length of the slope on your drawing should therefore measure around 13.2 cm and when you use the scale of 1:10:
- 13.2 × 10 = 132 cm or 1.32 m in real life
Answers in the range of 1.30 m to 1.36 m are considered accurate and correct.
Summary
In this section you have:
- applied your ratio skills to the concept of scale plans and drawings
- interpreted scale plans and decided upon a suitable scale for a drawing.