
In a game of word association what would you follow ‘mathematics’ with? Terror, boredom, difficult, nerds, geeks or history? I wonder how many people would associate mathematics with ‘everything’, ‘everywhere’, ‘life the universe and everything’ (not one word, I know). For some reason the world of maths seems to be thought of as a dusty dull subject far removed from the ‘real world’.
But this is crazy – maths is the most amazing subject, one that underlies almost every aspect of our everyday life. Personally I would associate maths with wonder, awe and perhaps just a little terror.
So when was the last time you unknowingly borrowed the work of a mathematician in your everyday life? If you are reading this article then you are at the computer: designed and programmed by mathematicians. Perhaps you like the cinema. The largest employer of mathematicians in the world is Pixar animations. Shrek just isn’t as funny when he’s flat. Maths makes his tummy round and his face comic. And it isn’t only animated films that need a mathematical touch. It takes a lot of maths to make modern special effects. It was some mathematician’s job to model the movement of Brad Pitt’s bottom as he leapt, ran and fought in the film Troy.
The mathematicians I know work on a spectacular diversity of investigations: from solving mysterious tropical fish deaths in a zoo to showing when salt water is better at combating fire than plain H2O. My cousin is a medical statistician and he is modelling the spread of various diseases. His colleagues will tell us how seriously to treat the impending Asian bird flu epidemic. And there are even mathematicians in the civil service. My friend is working out just how much benefit fraud is going on and how much would go on if we changed our benefit systems.
These are just a few examples of mathematics in our lives that immediately spring to mind, and I could go on and on. But this is not why mathematics fills me with wonder and awe. All I have said so far is that mathematics is a useful science, perhaps almost as useful as engineering. And that really would be missing the special nature of mathematics. It would be an unjust, miserly defence of this, the Queen of all the sciences. In fact,I would rather say that mathematics is God of science. It is omnipresent, omniscient and perhaps mathematics is also ‘begotten not made’.
A few years back, radio DJ Dr Fox confidently stated (when unwittingly caught out by the TV show Brass Eye) 'Now that is scientific fact. There's no real "evidence" for it but it is scientific fact.' showing, like many, an apparent misunderstanding of what makes a fact. I have never heard a scientist use the phrase 'scientific fact'. Scientists talk about evidence, evidence which supports hypotheses. Science can not give us definitive answers; there are always caveats, therre always further lines of inquiry. But mathematics is special – in fact it’s a unique realm where we have incontrovertible proofs. Classic Greek biology, physics and chemistry are not taught in schools today. Science has grown and improved over time. But Pythagoras' Theorem is as true today as it was when Pythagoras first dreamed it up.
Mathematics is a deep, powerful and infinite subject. It is a subject full of utter creativity. John F. Nash Jr , the mathematician protagonist of A Beautiful Mind, who suffered from delusions as a result of his schizophrenia, apparently said that the reason he believed such wild ideas was because they came from the same place as his mathematical ideas. It certainly is hard to describe how mathematical thought or inspiration occurs. Mathematical thought can be said to take place in another realm perhaps - Plato’s idealistic realm.
To look at all the aspects of mathematics that fill me with wonder would take far too long, but it is pretty simple to show you just one example, Proof by Induction. This is one of the powerful tools which mathematicians use to prove ‘statements’.
Supposing you want to prove a mathematical statement is true for all numbers (actually, we’ll stick to positive, whole numbers for this example). I suppose you could work it out, number by number, over and over again. But how many numbers would you have to do this for before you are sure it is true for all numbers? 10? 100? 1000? Ultimately, to be sure you’re going to be checking every number from here until eternity.
Proof by Induction, however, only takes two steps. We start by proving the statement for the first number. This is called proving the Base Case. The next stage is to prove what we call the Induction Step. We look at an arbitrary number. I am going to call the arbitrary number we are looking at k, if you don’t mind. If we can prove that when the statement is true for k it is also true for the successor of k then we are finished. Let me explain this further.
We have shown the statement is true for the first number. We have also shown that when the statement is true for one number it is automatically true for the following number. This means the statement is true for the number following the first number, in other words true for the second number. We have shown it is true for the number following the second number, so we know it is true for the third number. You can hopefully see how this logic shows you that the statement is true for all numbers.
A useful analogy is that of dominoes lined up.
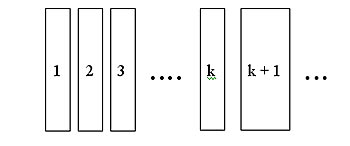
Suppose that:
- The first domino falls.
- If domino k falls then domino k + 1 will fall.
These two facts together tell us that all the dominoes will fall.
Here’s an example (if you don’t like algebra, don’t worry, I’ll try not to make this too scary!)
If you want to know what the sum of every number up to an arbitrary number is, is there a quicker way than just adding them all up? So, for example, what is the sum of all the numbers to 3?
1+2+3 = 6
OK, not that hard for that example, but what if you want to know the sum of all the numbers up to (say) 5,473?
1+2+3+4+5+6+7+8+9+10+11+12…
OK I’m bored typing this out already!
A clever chap called Gauss comes along and says the sum of all the numbers to n is equal to a half of n multiplied by n+1. He writes this down like this:
1 + 2 + …+ n = ½ x n x (n+1)
(Here n is bigger than or equal to 1)
Let’s check if Gauss is right when n is 3. Is it true that 1 + 2 + 3 = ½ x 3 x 4? This is true, as 1 + 2 + 3 = 6 and ½ x 3 x 4 = 6. But working out if this formula holds for each and every number would be both dull and impossible, an enticing combination! We can prove Gauss is right using proof by induction instead. How does it work for our example?
We start by proving the statement for the first number. In our example the first number is 1 (in mathematical terminology the Base Case is n = 1). The left hand side equals 1 and the right hand side equals ½ x 1 x 2, which is also 1. So the statement is true for the first number. We have proved the Base Case.
Now let us see if we can prove the induction step for our example. (This will involve a bit more algebra). We suppose the statement is true for the arbitrary number k.
So we assume:
1 + 2 + …+ k = ½ x k x (k+1)
Can we show the statement is true for the next number? Can we show it is true for k + 1?
We are aiming to show that the equation is true if we add (k +1) to the left hand side of the equation above, and also replace k with (k+1) on the right hand side:
1 + 2 + …+ k + (k + 1) = ½ x (k+1) x ((k+1) +1)
In other words:
1 + 2 + …+ k + (k + 1) = ½ x (k+1) x (k+2)
Let’s start with the left hand side of the equation.
1 + 2 + …+ k + (k + 1)
What is this equal to? Well, we have assumed the following:
1 + 2 + …+ k = ½ x k x (k+1)
So let’s use this information.
1 + 2 + …+ k + (k + 1) = (½ x k x (k+1)) + (k + 1)
I have taken the left-hand side and substituted the bold expression for the italicised expression. I can do this because the two expressions are equal. Now let’s tidy up what we have on the right-hand side of the new equation. How many (k + 1)’s do I have? The right-hand side of the equation says that I have ½ x k of them and another one. This can be written more simply as:
1 + 2 + …+ k + (k + 1) = ((½ x k) + 1) x (k+1)
We can tidy up the right-hand side still further to give:
1 + 2 + …+ k + (k + 1) = ½ x (k+2) x (k+1)
This is what we were aiming to show and we have shown it. We have proven the induction step and now we can say:
For any number n 1 + 2 + …+ n = ½ x n x (n+1)
Did that convince you? Think of our analogy of the dominoes. We proved the base case, the first domino fell down. Then we showed that if any domino falls down then the next one will also fall down. That is we showed that when:
1 + 2 + …+ k = ½ x k x (k+1)
1 + 2 + …+ k + (k + 1) = ½ x (k+1) x (k+2)
is also true.
You may not have liked some of the algebra steps but that doesn’t matter. The important thing to realise is that we have gained an infinite amount of information out of just two steps.
I’ll leave you with a brain teaser. No algebra this time. What is wrong with this proof by induction? The statement we shall prove is ‘All people are the same height’.
First I prove the Base Case. I am as tall as myself. This is certainly true.
Next, we prove the induction step. Take an arbitrary number of people, that is, we have a group with k people in it. If we assume that any group containing k people are the same height then it is our job to prove that any group containing one more person will also all be of the same height.
Assume any group of k people are the same height. Imagine them all in a room together. What about the next person? They enter the room. Send one of the original people out of the room. Now we are back to a room of k people. We have assumed that any group of k people are the same height. So our new person is the same height as the others. Bring back in the person who left the room. Now we have k + 1 people in the room and they are all the same height.
By induction, all people are the same height.
Can you see what is wrong with this proof? Is the concept of induction at fault? Or, could I have used it incorrectly somewhere?
I hope you can see that mathematics takes your mind to new places. It stretches and teases your brain. You can use it to play or to prove deep and powerful facts about the world. It truly is the Queen of Science.
Rate and Review
Rate this article
Review this article
Log into OpenLearn to leave reviews and join in the conversation.
Article reviews