As a pure mathematician, I've always been uncomfortable with the uncertainty in statistics. I work in the realm of absolute certainty. Certainty can persist for all time, and perhaps we could say, certainty can even persist outside of time. I can sketch a picture proof of Pythagoras’ Theorem and know that nothing can knock the proof down.
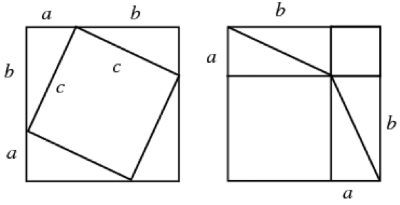
Since it's so quick and beautiful, allow me to explain how these two pictures prove Pythagoras’ Theorem.
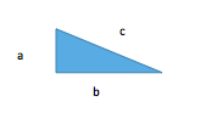
Pythagoras’ Theorem says that, given a right-angled triangle, the sum of the square of the short sides is equal to the square of the long side.
That is, if we have a triangle with sides of length a, b, c as shown, then c2 = a2 + b2
On the left, we have a big square which has side length a + b and so its area is (a +b)(a +b)
Depending on how long it is since you have had to do algebra, I can ensure you that:
(a +b)(a +b) = a2 + b2 + 2ab
But we also know the area of the little square and the triangles.
Each triangle is ½ ab.
We have four of them, so the area of the four triangles together is 4 x ½ ab = 2ab
The area of the smaller square is c2
So we could describe the area of the big square, as the area of the small square, plus the area of the four triangles.
c2 +2ab
Now we know that the area of the big square can be written in two ways, that is:
a2 + b2 + 2ab = c2 +2ab
We can simplify this to the well-known expression for Pythagoras’ Theorem.
a2 + b2 = c2
To me, this has a nice 'ta-da!' reveal to it. It's satisfying, we can put the question to bed and move on. So you can imagine how I squirm when I deal with the uncertainty of statistics.
All this led me to a talk given by my colleague, Carol Calvert, titled ‘Data – love the uncertainty’. This was what I needed to learn. After the talk, I interviewed Carol and admitted my issues with uncertainty.
Carol's career in statistics started with teaching. After teaching secondary school Mathematics for some time, she moved on to local government, and then the national government within the Government Statistical Service.
Can you tell me about your background in statistics?
"In the Civil Service in Scotland, you move departments a lot and get to work with all sorts of experts. You might work with the fisheries and go out on the boats or within housing and work on population forecasting. I worked with Social Services and moved to education (with some stops in between). This movement means you learn a great deal.
Statistics in Social Services covers areas such as how many children are in care. Where are they? Are any regions giving rise to unusually high instances of referrals? How often are community service orders used and do offenders re-offend?
My own passion was education, and so I worked in both the Schools Inspectorate and the Further Education Funding Council. We help to monitor the examination results of the schools and other education providers. The sorts of questions we would investigate are:
Given the background of the students in this school, have they performed as you would expect? A good analysis can look beyond absolute terms. It can show where schools have performed well in absolute terms, but also not well given their cohort of students and the converse can also be found. Once you have this information you can begin to ask what is this school doing right that can be replicated?
It sounds like the data is reliable and well understood. Where does uncertainty come into this?
The talk that you came to was really about the different places I had used Soundex. Soundex is an algorithm that was first patented in 1918 and has been under continual development since then. Soundex allows you to iron out some of the uncertainty in the datasets that are primarily due to the different spelling of names.
It all began with Americans trying to track their family trees. America has had a great deal of immigration and when you track most family trees, there will be immigration records somewhere along the way.
People arriving in America spoke all kinds of languages. Their names were recorded by people who didn't speak the newcomers' language and gave them various different spellings. This makes compiling a family tree quite a serious piece of detective work.
How does Soundex work?
Well, there are many versions but basically one of the most straightforward methods will replace a name by a single letter and then 3 digits. So “Ashcroft” and “Ashcraft” will both get coded as A261; “Rupert” and “Robert” both get coded as R150. Soundex is a set of rules which tells the computer to replace which letters, in which combinations, by which digit. Wikipedia, as so often, is a good starting point for more details.
I first came across Soundex when the Scottish Qualifications Agency used it within their processes for matching student results together. It was needed because, at that time, the student identifier was issued each year, so it has hard to provide one certificate for a student if the student had taken examinations in different years. I borrowed their excellent idea and used it to help me match the equivalent of GCSE results and A-level results, where students moved schools, to get a measure of how well students had done at the equivalent of A level given their prior attainment.
Following this, I used Soundex when I was working for the Department of Work and Pensions (DWP). I wanted to make it possible to be able to match the data held by DWP with that held by the tax office (HMRC). Government departments do not routinely match data. It is legally complex and so legislation had to be in place so we could perform the matching of these data sets. This was an important piece of work to allow new understanding of the needs of people, as well as to enable benefits to top up pay from employment much more flexibly. One example of a benefit which was directly supported by this matching was the introduction of universal credit.
How did you do the matching?
First of all, I never relied on a single source. Some sources are more reliable than others. If all the sources agree, then we can be confident that the two records have matched. If the sources differed, then you would worry.
In this specific case the best source to match records is the National Insurance (NI) number, then items like date of birth, gender and address. If the NI agree on the DWP record and HMRC record then you wouldn’t worry if there had been an address change or even a surname change. However, if the postcode, date of birth and surname are the same but the NI numbers are different, then you would look into this further.
When performing a matching with such large data sets, you generate a number of categories that require further investigation due an incomplete matching. For each of these categories, you would take a small sample (small in this case will be over 300 cases), and you look into these cases with great detail and care. Looking at this sample allows you to give ‘weight’ to each of the data sources. So the NI number may give you the correct record 95% of the time when you see this particular matching anomaly, and in the future, you can attach a likelihood to record matchings based on this ‘weight’.
Then you monitor the record matching process for a few years. In that time, you check whether the ‘weights’ (or likelihood, if there is a match) need tweaking. After a few years, you can review the process less frequently.
All this talk of records not matching reminds me of the dystopian film ‘Brazil’. The main character is found guilty of a crime as his name was incorrectly selected by the court. Should we be worried about the ways in which our data is used and by incorrect matchings like this?
We should always be worried about how our data is being used. Really you should be worrying about correct matchings of datasets. There are organisations with access to large amounts of our data. When they match datasets they can learn more about you than you may never have wished to tell them. It is very important that we learn more about how our data is being used. Some organisations sell your data to third parties.
But if data matching can have worrying consequences, then why do we allow organisations to do this at all?
Well, other organisations have used data matching for very good purposes. A data matching in the US showed that, in one region, a water company was piping lower quality, dirtier water to districts where ethnic minorities lived and sent high-quality water to white areas. A class action was brought and the injustice was rectified.
We are just beginning to see the potential of big data and the matching of data sets. There will be many unforeseen consequences of this new technology – both positive and negative.
Statistics are developing as a result of what technology can allow us to do. There will be new and exciting possibilities in the future. It's very much an area of growth.
Thanks for providing insight into how you can work with uncertainty robustly, and for showing me that it's "certainty" that I should be keeping a watchful eye on, rather than worrying about a bit of "uncertainty" in statistics.
Rate and Review
Rate this article
Review this article
Log into OpenLearn to leave reviews and join in the conversation.
Article reviews