4 Addition
If you are working out a budget, checking a bill, claiming a benefit, assessing work expenses, determining the distance between two places by car or any other everyday calculations, you will probably need to add some numbers together. Consider the following questions.
- How much is the bill altogether?
- How much will your holiday cost now that the total price of your airfare has increased by £50 due to fuel surcharges?
- Five more people want to come on the trip: What is the total number of people booked on the bus now?
- What is the cost plus VAT?
All the questions above involve addition to work out the answer. The key or ‘trigger’ words that indicate addition are in bold. The process of adding numbers together may also be referred to more formally as finding the sum of a set of numbers.
Something that you probably take for granted is that when you add two numbers together, it does not matter which order do this in, for example 2 + 3 gives the same answer as 3 + 2. In mathematical terms, we say that addition is commutative. Not every operation will possess this property, for example 5 − 3 does not equal 3 − 5.
There are a few ways that you can carry out addition on paper, in your head or using a calculator for more complicated sums. You may already feel comfortable with adding on paper, which is great, but here’s a quick overview just to make sure.
To add numbers in the decimal system, you write the numbers underneath each other so that the decimal points and the corresponding columns (or place holders) line up. Then you add the numbers in each column, starting from the right. Remember that when you are adding, if the sum from one column is larger than 10, you will need to carry into the next place holder.
For example, to add 26.20, 408.75 and 0.07 together, first check you’ve got the calculation lined up correctly, with the decimal points below each other. It is also a good idea to put the decimal point in the answer line too, so you don’t forget at a later stage.
Now, look at the numbers starting with the far right column: 0 + 5 + 7 = 12. So you write down a 2 underneath these figures and carry the 1 from the 12 to the next column.
Then move one column to the left: 2 + 7 = 9 – but don’t forget that 1 you carried over. So that makes 10 and should be written as a 0 in the tenths column with 1 carried over. The next column has 6 + 8 + 0 – and the one you’ve carried again. This equals 15, so put five down in the units column and carry the 1.
For the next column the sum is 2 + 0 plus the carried 1 to make 3. Nothing to carry this time! Just write down the 3. The final column just has a four, so all you need to do here is write down that four in the answer line and now you have your answer: 435.02.
Now try this activity on adding up items for a bill.
Activity 3 Checking a bill
Imagine you have bought three items costing £24.99, £16.99 and £37.25 from a mail order catalogue and the postage is £3.50. Start by rounding these prices to the nearest pound and working out an estimate for the total bill in your head, or on paper.
Answer
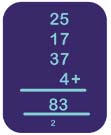
You may have your own method of working things out in your head that works fine for you. If so, there is no need to change how you do this, but you might find the following method useful to work through. The four rounded prices are £25, £17, £37 and £4. To find an estimate for the total cost, add the four rounded prices together.
This is easier to do if you split each number apart from the first one, into tens and units, so 17 can be split into 10 + 7 and 37 into 30 + 7. This makes the sum much easier to work out in your head and the sum then becomes 25 + 10 + 7 + 30 + 7 + 4.
Then, working from the left and adding each number in turn, you can say, ‘25 and another 10 makes 35; another 7 gives 42; another 30 gives 72; 7 more makes 79, and another 4 gives 83’. The answer is 83, so the total bill will be approximately £83.
You can then check your estimate by writing out the problem without rounding and performing the calculation again to give the accurate bill.
You can see that the estimate of £83 was very close to the exact total of £82.73. Now you can be confident in your answer.
The next section will look at subtraction.