1 Fractions and decimals
You use fractions every day even if you're not really thinking about it. For example, if somebody asks you the time it could be half past 2 or a quarter to 6. The half and the quarter are parts of an hour; in other words they are fractions of a whole.
The number at the bottom of the fraction tells you how many parts the whole one has. So, has two parts in the whole one and has 4. The number at the top tells you how many of these parts there are. Hence, is 1 lot of 2 parts. You’ll be looking at this again in more detail in Week 3.
Since fractions are parts of a whole, just as decimals are, this means that you can relate fractions and decimals. Here you will only be dealing with fractions that are easily shown in a place value table.
So, say you needed to write out 2 and (three-tenths) as a decimal. The whole part is 2 and the fractional part is . Remember in order to separate the whole number from the fraction you use a decimal point, with the part of the whole number to the right. So, you would write the 2 to the left of the decimal point and the fractional part to the right of the decimal point. Thus, it would be written as 2.3. If you were dealing with on its own, you would need to show that there were no whole parts by showing a zero to the left of the decimal point. is therefore written as 0.3.
Now you’ve seen a few examples, it’s your turn to have a try yourself in the next activity. You can use a place value table if it helps you.
Activity 1 Fractions to decimals
a) Rewrite each of the following fractions as a decimal number.
- i.
Remember: if the number does not have a whole number part, a zero is written in the units place. This makes the number easier to read (it’s easy to overlook the decimal point).
Answer
- i.
- ii.
Answer
- ii.
- iii.
Answer
- iii.
- iv.
Answer
- iv.
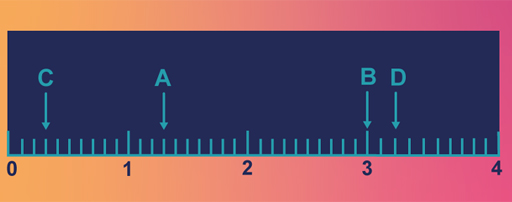
b) Match the numbers below to the letter shown on the number line in Figure 1.
Two lists follow, match one item from the first with one item from the second. Each item can only be matched once. There are 4 items in each list.
-
B
-
C
-
A
-
D
Match each of the previous list items with an item from the following list:
a.
b.
c.
d.
- 1 = b,
- 2 = a,
- 3 = d,
- 4 = c
Now, you’re going to turn your attention to rounding numbers, and making estimates. Understanding place value will help with this, but you’ll also investigate the idea of decimal places when rounding.