6.1 Maths cycle in practice: insulating the attic
Work through this real-life problem using the maths cycle.
Step 1: Describe the problem
My father has recently moved into an old terraced house that needs insulation in the attic. I have volunteered to take care of this task. Although I think it’s going to cost less to put in the insulation myself, my dad can get a grant from local government if the insulation is installed by an approved contractor. But which is the cheaper option?

Step 2: Collect information, make assumptions and simplify the problem
Now I need to write down what I know and what I still need to find out. After measuring the attic space and joists, visiting a DIY shop, contacting the local government department about the grant and local contractors for quotes, I wrote down the list given in Table 4.
| I know: | I want: |
|---|---|
| The attic is approximately 825 cm by 900 cm. | To find the cheaper option |
| Each joist is 5 cm wide. | |
| There are 17 joists. | |
| The insulation fits perfectly between the joists. | |
| A £200 grant is available. | |
| The cheapest quote from a contractor is £650. | |
| The insulation comes in rolls that are 40 cm wide and 800 cm long. | |
| Each roll costs £15 but there is a special 3 for 2 offer at the moment. | |
| I need safety glasses, a face mask and gloves costing £40 to install the insulation. |
Step 3: Do the maths! (Part 1)
This is a complicated problem, so a useful strategy would be to break it down into more manageable chunks. There are two separate problems:
- How much would my father have to pay if he got the £200 grant and used the contractor?
- How much would the ‘do-it-yourself’ option cost? Broken down into:
- How much insulation will I need?
- How much will the materials cost?
In Activity 6, you will focus on the first question: how much would my father have to pay if he got the £200 grant and used the contractor?.
Activity 6 The contractor’s costs
How much will it cost if the contractor installs the insulation and the grant is used?
Answer
The contractor charges £650 and the grant is £200
So, overall cost = £650 − £200 = £450.
So the total cost using an approved contractor is £450.
Now you know how much it would cost if a contractor installed the insulation, you want to know how much the ‘do-it-yourself’ option will cost to allow you to make a comparison. You should start by working out how much insulation is required.
Step 4: Do the maths! (Part 2)
This means working out how many rolls are needed. In this case a diagram will probably help.
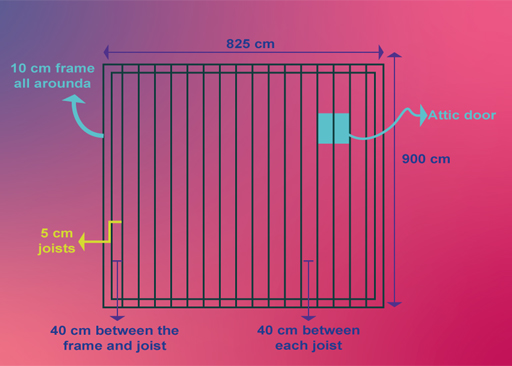
Figure 5 shows a rough plan of the attic.
Note: the attic door is in the floor and will be covered by insulation. The insulation will later be cut to allow the door to open.
As the insulation fits perfectly between the joists, as well as the frame and outer joists, the amount of insulation needed will be easy to calculate.
One roll of insulation is 800 cm long.
The length of the attic minus the frame at each end is 900 cm − 10 cm − 10 cm = 880 cm.
So one roll between the joists is not quite enough to do the job because there is an extra 880 cm − 800 cm = 80 cm that need to be covered between any two joists.
Activity 7 How many rolls do I need to buy?
Use the information given above to work out how many rolls of insulation are needed.
Answer
First, you can see I will need 18 rolls to lie between the joists and between the frame and outer joists.
However, you know that each roll leaves an extra 80 cm not covered. This happens 18 times, so I am short 18 × 80 cm = 1440 cm. Since one roll is 800 cm, I will need to buy two more rolls of insulation (1440 cm ÷ 800 cm = 1.8). Therefore, I need a total of 20 rolls of insulation.
You’re nearly there now – just one more step to finally work out the DIY cost.
Step 5: Do the maths! (Part 3)
Activity 8 The price of doing it yourself
Now work out the DIY cost using all the information you’ve gathered and worked out.
Remember:
- Each roll costs £15.
- There is a ‘three-for-two’ special offer.
- I will also need to buy some safety equipment costing £40.
- I need to buy 20 rolls of insulation.
Answer
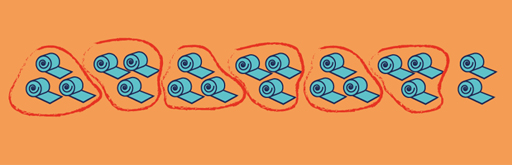
Since I need to buy 20 rolls of insulation, I will be able to take advantage of the ‘three-for-two’ offer. So for every three rolls I purchase, I only pay for two rolls.
So cost of three rolls = £15 × 2 = £30
To determine how many times I will get to take advantage of the offer, a picture can be used.
Since there are six sets of three rolls, it will cost £30 × 6 = £180. Unfortunately, the two additional rolls won’t be on offer, so the insulation will cost £180 + £15 + £15 = £210.
Finally, the safety equipment is £40. This puts the total cost at £210 + £40 = £250
You can now move onto the final step in the problem solving cycle – interpreting the answer
Step 4: Interpret the answer
Now you can make an informed decision.
Should I hire the contractor and use the grant for placing the insulation in the attic, or should I do it myself?
The cost of using an approved contractor is £450. The price of installing the insulation myself is £250. Based on these values, I should choose the DIY option. However, I may also take other factors into consideration when coming to a decision, such as the convenience of undertaking the work myself. So, the mathematical solution may be just one of several issues to consider.
Well done for working your way through this more complex problem. If there were points when you got stuck, don’t worry this happens to us all. The final section will summarise the techniques you used to help solve this last problem.