1.1 Folding paper

It is possible to use a simple piece of paper to help understand fractions. Here you’ll see how.

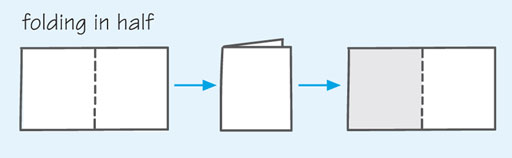
Take a piece of paper and fold it in half, creasing along the fold. Open it up and shade the left-hand side. You don’t have to fill this completely, just make sure that one half is clearly different from the other.

Figure 1 Folding a piece of paper in half

Show description|Hide description

A piece of paper shown at three different stages. At the first stage the paper is blank with a dotted line splitting the piece of paper in two. At the second stage, the piece of paper is folded along the dotted line, so the piece of paper is folded in half. In the third stage the piece of paper looks the same as it did in the first stage, but this time the left-hand side of the piece of paper is greyed out.

Figure 1 Folding a piece of paper in half

Since your paper has been divided into two equal parts, each piece is half of the original. This fraction is written as and read as ‘one-half’.

The ‘bottom number’ is called the denominator. It tells you how many parts of the whole one has been divided into. For example, if it’s a four, then the whole thing (piece of paper, cake, etc.) has been divided into four parts.

The ‘top number’ or numerator tells you how many of those parts you have. So for , it means the whole thing is divided into four parts, and you have three of them.

The numerator and denominator are separated by a line known as the fraction bar.

Figure 2 Defining a fraction

Show description|Hide description

The fraction ‘one-half’ is shown as a one over a two, with a horizontal line between the two numbers. An arrow points to the one with the comment ‘top number is called the numerator and is the number of shaded pieces’. An arrow points to the two with the comment ‘bottom number is called the denominator and is the total number of pieces’.

Figure 2 Defining a fraction

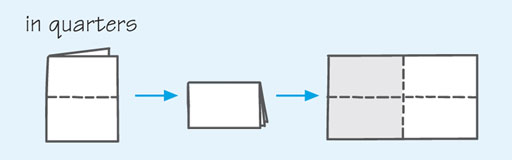
Now fold your piece of paper back along the original crease and then in half again along the long side. If you open up the paper, you should see four pieces of the same size, with two of them shaded.

The paper is now divided into quarters, and the fraction of the paper shaded is .

Figure 3 Folding a piece of paper into quarters

Show description|Hide description

A piece of paper folded in half, then in quarters and opened up with the two left-hand quarters (i.e. one half) shaded.

Figure 3 Folding a piece of paper into quarters

Since you haven’t altered the shading in any way, this demonstration shows that one half is equal to two quarters:

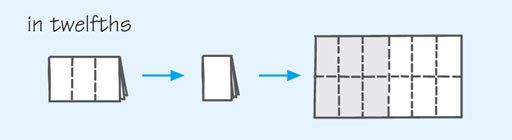
Now fold the paper back into quarters along the crease lines, and then fold into three equal pieces or thirds along the long side. If you now open up the paper you can see that there are 12 equal pieces. These pieces are ‘twelfths’, of which six are shaded, so of the paper is shaded. This fraction also represents the same amount as .

Figure 4 Folding a piece of paper into twelfths

Show description|Hide description

A piece of paper folded in quarters, then in twelfths, with each twelfth marked by a dotted line. Opened up to a full piece of paper, it shows six twelfths shaded on the left-hand side shaded.

Figure 4 Folding a piece of paper into twelfths

You can continue to fold the paper into smaller and smaller pieces. Each time you open up the paper it will be divided into smaller fractions but half of it will still be shaded. The fractions that represent the shaded part are all equivalent to each other.

So .

Now it’s time to look at equivalent fractions in more detail.