2.1 Working with equivalent fractions

This section shows you a slightly different way to help you visualise the process of finding equivalent fractions and simplifying fractions.

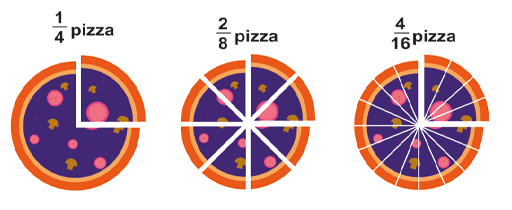
Figure 7 shows three pizzas. You can see that of a pizza is the same as of a pizza, and also the same as of a pizza. So all these fractions are equivalent and can be simplified to . This is similar to the example of folding a piece of paper.

Figure 7 Pizza maths

Show description|Hide description

Three pizzas: the first pizza has a quarter section cut out of it and is labelled ‘one quarter pizza’; the second pizza has two one-eighths sections cut out of it and is labelled ‘two-eighths pizza’; and the third pizza has four one-sixteenths sections cut out of it and labelled ‘four-sixteenths pizza’. The amounts cut out are equivalent to each other so the figure shows that one quarter is the same as two eighths, which is the same as four sixteenths.

Figure 7 Pizza maths

Below are some examples for you to try but before you do that you might like to view this video on equivalent fractions.

Download this video clip.Video player: swm_1_s3_equivalent_fractions.mp4

Show transcript|Hide transcript

Transcript

NARRATOR:

Take 2/3. Can you think of any other fractions which are equivalent to this? Well, to do this, it's first helpful to visualise what 2/3 is. So let's draw a box, which we would divide into three equal sections. And so, 2/3 would equal two of those three equal sections.

So now, there are a couple of things you can do to find equivalent fractions of 2/3. You can take the box and draw a horizontal line across the whole box to divide each of the three sections into two parts. So now, how many equal sections do we have? We have six equal sections. And how many of those equal sections are shaded in now? We can see four of those sections are shaded in.

So here, we can see that 4/6 is the exact same fraction of the whole as 2/3. These are equivalent fractions. We can say that 2/3 is equal to 4/6.

And now, let's find another equivalent fraction of 2/3. Instead of dividing each of the three pieces into two parts, we can divide these into three parts.

So, I can draw two more horizontal lines here. So now, I have divided what was in three equal parts into three times as many parts. I now have nine equal parts. And how many of those are shaded in? We have six shaded in. So 2/3 is equal to 4/6, which is also equal to 6/9. All three of those are equivalent fractions.

Now, take this second example. Say you have 6/10. This can be shown as a block of 10 equal sections with six shaded in. If you were to pair each square up so that there were only five pieces all together, you can see that there are now only three blocks painted. But it still covers the same area. We then know that 6/10 is equal to 3/5.

End transcript

Download

 

Remember, when carrying out the activity there may be more than one way to arrive at the answer, and you must divide or multiply both the numerator and the denominator by the same number at each step. Note it has to be multiplying or dividing – they are the only operations that make this work.

Activity 1 Equivalent fractions

Timing: Allow approximately 10 minutes

(a) Use your knowledge of equivalent fractions to determine the missing numbers. Remember that both the numerator and the denominator must be multiplied or divided by the same number.

(i)

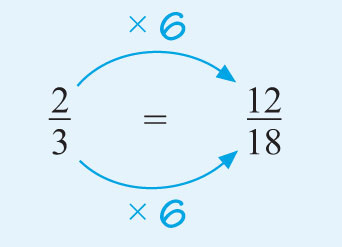
Hint: the denominator of the fraction on the left is 3. What do you have to multiply it by to get 18? Remember that if you multiply the denominator by a particular number, you must do the same to the numerator to keep the fractions equivalent.

Answer

The 3 is multiplied by 6 to reach 18, so this is the number that is used to multiply both the numerator and the denominator. The missing number is 12.

Figure 8 is equivalent to

(ii)

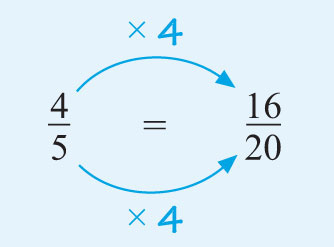
Answer

Similarly, since 5 × 4 = 20, multiply the numerator and the denominator by four. The missing number is 16.

Figure 9 is equivalent to

(b) Which of the following three fractions are equivalent to each other?

(i)

(ii)

(iii)

Answer

Multiplying the numerator and the denominator of the first fraction by five gives:

Figure 10 is equivalent to

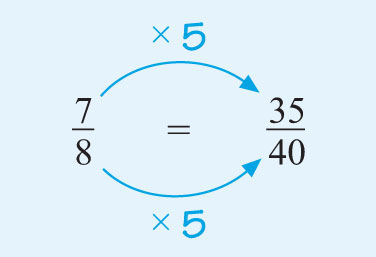
Only the two fractions labelled (i) and (ii) are equivalent.

You cannot create from by multiplying the numerator and the denominator by the same number.

If you multiply by 7 you get , which isn’t . If you multiply by 8 you get , which isn’t , either.

(c) Simplify the following fractions:

(i)

(ii)

(iii)

(iv)

Hint: what number can divide exactly into both the numerator and the denominator of each fraction? Remember, there could be more than one option or step to fully simplify these.

Answer

(i) Dividing the top and the bottom by 2 gives .

(ii) Dividing the top and the bottom by 10 (or by 5 and then by 2) gives .

(iii) Dividing the top and the bottom by 9 and then by 3 gives .

(iv) Dividing the top and the bottom by 4 and then 3 gives .

(Of course it does not matter which number you divide by first, and there are even more choices than the ones shown.)

If you find it difficult to spot the numbers to divide by, try to work systematically by trying 2, 3, 5 … in turn.

In the next section, you can try an activity where you need to write your own fractions from information you are given. Remember to show these in their simplest form – this is the way that fractions should be shown.