4.1 Improper fractions
Improper fractions are fractions in which the numerator is greater than or equal to the denominator. You can think of these as ‘top-heavy’ fractions, such as and . These mean 5 halves, and 8 fifths respectively.
Improper fractions are another way of showing mixed numbers. So, can be rewritten as an improper fraction to give . You can again imagine this in terms of pizzas. If you have two and one third pizzas, and cut each of the whole pizzas into thirds, then how many thirds of a pizza will you have?

In this case, the total number of thirds will be , showing that can indeed be written as .
Now think about how seven thirds was found. Because there were two whole parts broken into thirds, plus one extra third, 2 was multiplied by 3 to calculate how many thirds there were in two whole pizzas, then 1 was added. Since these are all thirds, the 7 was placed over the 3 in fractional notation. This can be worked out as follows:
This works for any mixed number that you need to convert into an improper fraction. So, the rule is:
You can also change improper fractions back into mixed numbers. For example, for imagine some pizzas have been cut into eight equal slices (eighths), and that you have 17 slices, but you don’t know how many whole pizzas this makes. You know that eight slices make one whole pizza, and that two pizzas would be 16 slices (2 x 8). There would be one-eighth (one slice) left over. So, . You can also carry out the division implied by the fraction:
Since eight goes into 17 at most two whole times, and there is one out of eight parts left over, this again gives .
One of the best ways for you to cement new ideas in your mind is to practise them. Try the next activity for mixed numbers and improper fractions.
Activity 5 Mixed numbers and improper fractions
(a) Change the following mixed numbers into improper fractions.
i.
ii.
iii.
Hint: if you are having trouble with this, did you try using a picture?
Answer
(i) You are working in quarters, so using ‘pizza maths’ you need to divide each pizza into four to give you Figure 14.
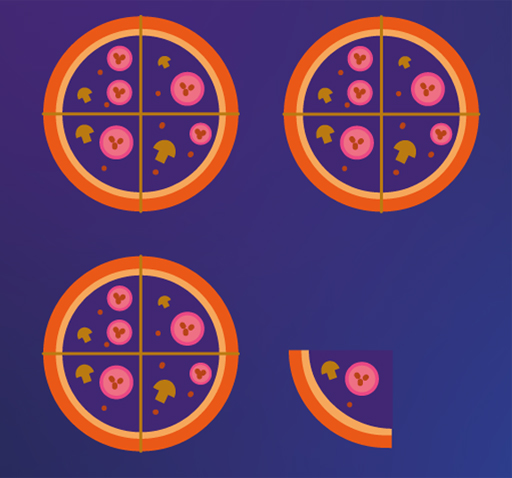
As there are four quarters in each whole, three wholes will give 3 × 4 = 12 quarters. The one extra quarter makes 13 quarters overall.
Thus, .
(ii) You could use the following shortcut to solve this one:
(iii) There are eight eighths in each whole, so seven wholes will give 56 eighths (7 x 8). The extra three eighths makes 59 overall, so the fraction is . Hence, .
(b) Change the following improper fractions into mixed numbers.
i.
ii.
iii.
Answer
i.Since 4 × 5 = 20, 20 fifths will make up 4 wholes. This leaves an extra 3 fifths, so the fraction is . Thus, .
ii.Let’s try using long division:
Since 2 × 7 = 14, 14 sevenths will make up two wholes. This leaves one seventh over, so the fraction is . Hence, .
iii.Since 4 × 4 = 16, 16 quarters will make up four wholes. This leaves one quarter over, so the fraction is . Consequently, .
Well done for completing this activity with mixed numbers and improper fractions. You will need the skills that you have been practising here next week when you learn how to carry out calculations with fractions. You’ve got one last activity in the next section before finishing this week.
