2.3 Electromagnetic waves
Electromagnetic waves come in many forms, and they’re hugely important for modern life and technology. Radio waves transmit information across a range of frequencies, be it radio and TV programmes or mobile phone calls. Microwaves are used to heat food and to navigate planes and ships by radar. Visible and near visible (infrared, ultraviolet) light keep us warm and allow us to orientate ourselves in the world. X-rays and gamma rays are used in medical imaging and radiological therapy.
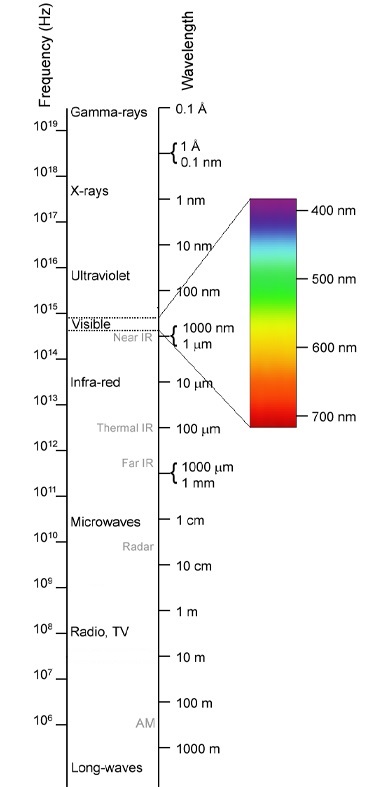
The travelling electromagnetic wave consists of oscillating electric and magnetic waves. The difference between radio waves, microwaves or visible light is just their wavelength or frequency. The size of an antenna gives you an idea of the wavelength for radio waves, while the wavelength of visible light is around a thousandth of a millimetre. Regardless of their wavelength or frequency, all electromagnetic waves travel at the speed of light (which is defined to be exactly 299,792,458 metres per second, so about 300,000 kilometres per second, in vacuum). Figure 5 shows the electromagnetic spectrum, so you can see some of this in context.
French physicist Louis de Broglie hypothesised in 1924 that all matter demonstrates wave properties; such behaviour was soon demonstrated in experiments, and de Broglie won the Nobel Prize in Physics in 1929. The ‘de Broglie wavelength’ is given by Planck’s constant divided by the momentum (mass times speed) of the particle.
But what is ‘Planck’s constant’? It’s a value derived from the energy of a photon, relating its energy to its frequency. That is, if you take the energy of any photon (measured in Joules) and divide it by the photon’s frequency (measured in meters per second), you get a constant. This is called Planck’s constant, and is usually denoted by the letter h. It’s one of the fundamental constants of nature which, like the speed of light, has been defined with an exact value. This value is h = 6.62607015 × 10-34 J-s (Joule-seconds), which is a very small number indeed (10-34 is a kind of shorthand; to write it out fully, there would be 33 zeroes after the decimal point before the first non-zero digit).
The wavelength of these ‘matter waves’ is absolutely tiny as a result, and cannot be observed outside the world of molecules, atoms and subatomic particles. This brings us to the realm of quantum theory. But before entering this intriguing world, let’s look at a crucial property of wave motion, which is important both in the classical and in the quantum world.