4 Your time is not my time

The consequences of Einstein’s insight are profound. This section will look at just one of them, namely that time flows differently for different observers. The following video shows how an imaginary ‘light clock’ can be used to illustrate this rather strange idea.

Download this video clip.Video player: Video 4

Show transcript|Hide transcript

Transcript: Video 4 60-Second Adventures in Astronomy: Special Relativity

DAVID MITCHELL

60 Second Adventures in Astronomy. Number ten: Special Relativity.

[MUSIC PLAYING]

Does time fly when you’re having fun? In 1905, Albert Einstein introduced the theory of Special Relativity, which said that if the speed of light is constant, then people must experience time differently.

Which may sound impossible, but Richard Feynman later showed that you can prove it with just lights and mirrors. If you set up two mirrors, one of which had a flashbulb and a detector on it, you could build a clock which ticked every time the flash was reflected back to its original source. It would keep time perfectly, though it would make a slightly annoying alarm clock.

But if you make this clock go past you very quickly, the light has further to travel, and since light always travels at the same speed, the moving clock runs slower than when it was at rest. So, though time might not fly when you’re having fun, a moving clock does tick more slowly than the observer’s stationary clock – which may have changed the way we see the universe, but doesn’t always make for a good excuse.

End transcript: Video 4 60-Second Adventures in Astronomy: Special Relativity

Download

Video 4 60-Second Adventures in Astronomy: Special Relativity

To examine this a bit further with the use of some maths, have a go at the following activity.

Activity 2 The ‘light clock’ thought experiment

Timing: Allow about 10 minutes

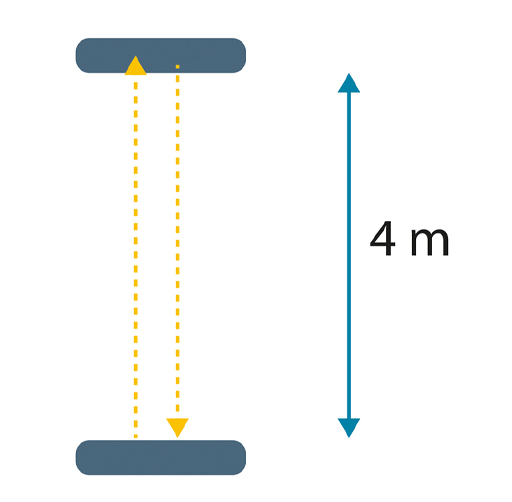
Imagine you have two mirrors, set four metres apart. A pulse of light bounces back and forth between the two, as shown in Figure 2.

Figure 2 Two mirrors set apart

Show description|Hide description

This diagram depicts two mirrors, marked as being four metres apart. A yellow arrow depicts the light bouncing between them.

Figure 2 Two mirrors set apart

If the speed of light is 3 × 10⁸ m/s, how long will it take the pulse to make the round trip of 8 metres?

To use this interactive functionality a free OU account is required. Sign in or register.

Interactive feature not available in single page view (see it in standard view).

Answer

This round trip of 8 metres is completed in about 27 billionths of a second, or 27 nanoseconds. By keeping count of the number of round trips, as the light ‘ticks’ between the mirrors, you’ve got a ticking clock!

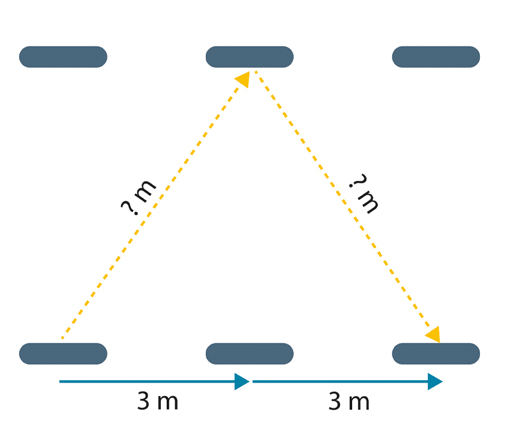
Meanwhile, an astronaut on a passing spaceship (here moving at 60% of the speed of light) watches our clock as she zooms past. Her view at three instants (Figure 3) is rather different. Because she sees the mirrors in motion, the pulse of light now has to travel a longer distance, which can be calculated.

Figure 3 An astronaut passes the clock

Show description|Hide description

This diagram depicts the clock from Figure 2, observed from three different positions, each three metres apart. The mirrors are still four metres apart.

Figure 3 An astronaut passes the clock

In the time for a return trip, the mirrors have moved by 6 metres. How far does the pulse now have to travel? Hint: note that the pulse is travelling along the hypotenuse of two identical right-angled triangles.

To use this interactive functionality a free OU account is required. Sign in or register.

Interactive feature not available in single page view (see it in standard view).

Answer

Pythagoras’ theorem tells us that the square of the hypotenuse is equal to the sum of the squares of the other two sides:

So for the first triangle, the pulse travels the following distance:

The round trip distance, then, is 10 metres.

How long does the pulse take to travel 10 metres?

Discussion

The speed of light for the astronaut is still 3 × 10⁸ m/s, so the time for the round trip is now

This is approximately 33 nanoseconds.

In these two scenarios, two people observe the same clock. One sees it tick every 27 nanoseconds, while the other sees it tick every 33 nanoseconds. A moving clock ticks more slowly than a stationary clock.

Although this activity used an imaginary light clock, this difference has nothing to do with the construction of the clock. It stems from the nature of space and time. This effect is known as ‘time dilation’ and it means that, in general, no two observers will agree on their measurements of time. But it gets stranger still. Because it’s the relative motion that matters, you would see an identical clock on the moving spaceship running slow for the very same reason.

That might be surprising (and even hard to believe), but time dilation is firmly within the realm of what we can and do know about time, and won’t be explored in more depth here. (If the topic intrigues you though, you may like to do some further independent learning – see what you can find out about the ‘twin paradox’.)